• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Ймовірність гіпотез. Формули Байєса

Нехай подія А може настати за умови появи однієї з несумісних подій В₁, В₂,... В_n, що створюють повну групу. Оскільки заздалегідь невідомо, яка з цих подій настане, їх називають гіпотезами. Ймовірність появи події А визначається за формулою повної ймовірності (див. п. 2):

.

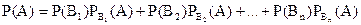Припустимо, що проведено випробування, внаслідок якого з’явилася подія А. Поставимо своєю задачею визначити, як змінилися (у зв’язку з тим, що подія А вже настала) ймовірності гіпотез. Іншими словами, будемо шукати умовні вірогідності

.

Знайдемо спочатку умовну ймовірність Р_А(В₁). За теоремою множення маємо

.

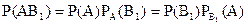Звідси

.

Замінивши тут Р(А) за формулою (*), отримаємо

.

Аналогічно виводяться формули, що визначають умовні ймовірності інших гіпотез, тобто умовна ймовірність будь-якої гіпотези В_і (і=1, 2, ..., n) може бути обчислена за формулою

.

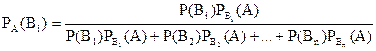Отримані формули називають формулами Байєса (по імені англійського математика, який їх вивів; були опубліковані в 1764 році)

Формули Байєса дозволяють переоцінити ймовірності гіпотез після того, як стане відомим результат випробування, внаслідок якого з’явилась подія А.

Запитання для самоперевірки:

1. Що називають добутком подій А і В?

2. Поясніть поняття умовної ймовірності.

3. Як визначити ймовірність спільної появи двох подій?

4. Які події називають незалежними?

5. Які події називають попарно незалежними?

6. Які події називають незалежними у сукупності?

7. Як обчислити ймовірність спільної появи декількох подій, незалежних у сукупності?

8. Як обчислити ймовірність появи тільки однієї з декількох незалежних подій?

9. Як обчислити ймовірність появи хоча б однієї події?

10. Яку формулу називають «формулою повної ймовірності»? Виведіть її.

11. Які можливості надає формула Байєса?

12. Покажіть, як за допомогою формули Байєса можна перевірити ймовірність гіпотез.

Читайте також:

1. Безпосереднє обчислення з використанням формули Ньютона-Лейбніца.
2. Введення формули в комірку.
3. Виведення формул для знаходження площі паралелограма, трикутника, трапеції. Формули для знаходження площ поверхонь просторових геометричних фігур.
4. Вітальні формули
5. Географічні фактори, які визначають поширення паразитів та ймовірність існування певних паразитарних систем
6. Геометрична ймовірність
7. Електронні формули
8. Завадостійкість і ймовірність передачі даних
9. Завдання теорії корисності і підхід Байєса.
10. Загальні хімічні формули
11. Із формули (5.4) випливає, що амплітуда результуючого коливання визначається не тільки амплітудами коливань, що додаються, а й змінюється залежно від різниці їхніх початкових фаз.
12. Ймовірність відхилення відносної частоти від постійної ймовірності в незалежних випробуваннях

Переглядів: 3755