• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Ймовірність відхилення відносної частоти від постійної ймовірності в незалежних випробуваннях

Знову будемо вважати, що проводиться n незалежних випробувань, в кожному з яких ймовірність появи події А постійна і рівна р (0<р<1). Поставимо перед собою завдання знайти ймовірність того, що відхилення відносної частоти від постійної ймовірності р за абсолютною величиною не перевищує заданого числа . Іншими словами, знайдемо ймовірність здійснення нерівності

. (*)

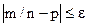Цю ймовірність будемо позначати так: Р(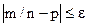).Замінимо нерівність (*) їй рівносильними:

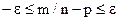або .

Перемноживши ці нерівності на додатній множник , отримаємо нерівності, рівносильні початковій:

.

Скористаємося інтегральною теоремою Лапласа у формі, указаній в зауваженні (див. 4.3). Поклавши і , маємо

.

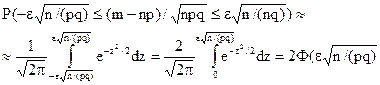Нарешті, замінивши нерівності, що знаходяться в дужках, рівносильною їм початковою нерівністю, остаточно отримаємо

.

Отже, ймовірність здійснення нерівності 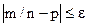приблизно дорівнює значенню подвоєної функції Лапласа при .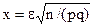

Запитання для самоперевірки:

1. Які випробування називають незалежними щодо події А?

2. Поясніть поняття «складна подія».

3. Виведіть формулу Бернуллі.

4. Сформулюйте локальну теорему Лапласа (Муавра – Лапласа).

5. При яких умовах застосовується локальна теорема Лапласа?

6. Сформулюйте інтегральну теорему Лапласа.

7. Як на практиці обчислити ймовірність того, що подія А з’явиться від 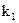до разів в 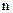незалежних випробувань, якщо ймовірність її появи в кожному випробуванні постійна і відмінна від нуля и одиниці?

8. Як обчислити ймовірність відхилення відносної частоти від постійної ймовірності в незалежних випробуваннях?

Читайте також:

1. Ne і ne – поточне значення потужності і частоти обертання колінчастого вала.
2. Аналіз результатів за відхиленнями
3. Банкрутство підприємства: причини, оцінка ймовірності настання та наслідки
4. Вади розвитку – це порушення внутрішньоутробного розвитку, відхилення від нормальної будови організму. Найлегші ступені вад розвитку називають аномаліями, найважчі – потворністю.
5. Визначення ймовірності перерви електропостачання і середньої кількості недоотриманої електроенергії.
6. Використання моделі Хікса – Хансена для оцінки відносної ефективності бюджетно-податкової і кредитно-грошової політики
7. Вимірювання частоти обертання.
8. Випадок непов’язаних(незалежних) вибірок
9. Випробуваннях характеристики міцності
10. Відносна частота. Стійкість відносної частоти
11. Відхилення від законів Г. Менделя
12. Відхилення від типових чисельних співвідношень і їх причини.

Переглядів: 2410