• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Взаємодія струмів і частинок з магнітним полем

Сила Ампера – цесила, що діє на елемент струму 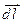у магнітному полі, визначається формулою

, (4.20)

або в скалярному вигляді

,

де α – кути меж векторами 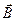і 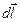(див. рис. 54).

Рис. 54

Розбиваючи провідник на елементи струму і визначаючи за формулою (4.20) силу, що діє на кожний елемент струму, можна визначити розподіл сил уздовж провідника, що діє на провідник зі струмом у магнітному полі.

Сила Лоренца – це сила, що діє на рухому заряджену частинку у магнітному полі. Вона визначається формулою

;

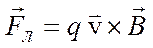або в скалярному вигляді

,

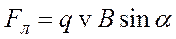де α – кут між векторами 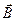і 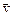(див. рис. 55).

Оскільки 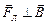, то сила Лоренца роботи не виконує і чисельного значення швидкості змінити не може. Вона змінює тільки напрямок вектора швидкості.

Контур зі струмом у магнітному полі. Якщо внести у магнітне поле контур зі струмом, то збоку поля на контур діє обертальний момент (див. рис. 56)

;

або у скалярному вигляді

,

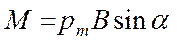де – вектор магнітного моменту контуру зі струмом, – вектор магнітної індукції, α – кут між векторами і .

Під дією обертального моменту 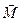контур обертається і встановлюється своїм магнітним моментом уздовж вектора магнітної індукції .

Робота з переміщення струму в магнітному полі. При переміщенні провідника зі струмом у магнітному полі сила Ампера, що діє на провідник зі струмом, виконує роботу

,

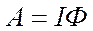де I – сила струму у провіднику, Ф – магнітний потік, який перетинає провідник при своєму русі.

Рис. 55

Рис. 56

Для прямолінійного провідника, що рухається перпендикулярно, лініям індукції однорідного магнітного поля,

,

де l – активна частина провідника (тобто та, що знаходиться у магнітному полі), S – пройдений шлях.

При переміщенні контуру зі струмом у магнітному полі виконується робота

,

де 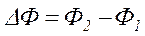– зміна магнітного потоку через контур, Ф₁ – початковий потік, Ф₂ – кінцевий потік.

Читайте також:

1. Активно взаємодіяти з навколишнім світом
2. Б- не збуджена ділянка мембрани , на яку діють електричні струми збудженої ділянки. Стрілками показано напрям струмів, кружечками – дійсне переміщення іонів.
3. Багатоманітність і взаємодія культур
4. Барометрична формула. Розподіл Больцмана частинок у зовнішньому потенціальному полі
5. Взаємодія
6. Взаємодія +Це єдність В. і в-ця.
7. Взаємодія алельних генів
8. Взаємодія важелів. Оцінка сукупного ризику, зв'язаного з підприємством.
9. Взаємодія гамма квантів з речовиною
10. Взаємодія гамма-квантів з речовиною
11. Взаємодія ДСМК з іншими аварійно-рятувальними службами.
12. Взаємодія електромагнітних випромінювань з речовиною

Переглядів: 978