
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Індивідуальні завдання
8.15. . 8.16. . 8.17. .
8.11. . 8.12. . 8.13. .
8.18.  . 9.1.
. 9.1. 

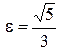 . 9.2.а)
. 9.2.а) 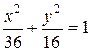 , б)
, б) 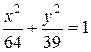 , в)
, в)  , г)
, г)  ,
,
д) 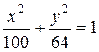 , е)
, е)  . 9.3.
. 9.3.  . 9.4.
. 9.4. 
 . 9.5.
. 9.5.  . 9.6.
. 9.6. 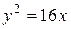 або
або 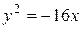 . 9.7.
. 9.7.  .
.
1. Знайти матрицю 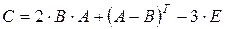 , де
, де  – одинична матриця третього порядку, якщо:
– одинична матриця третього порядку, якщо:
1. 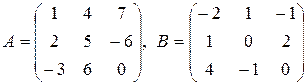 .
.
2. 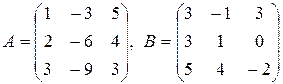 .
.
3. 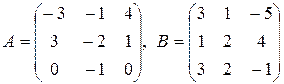 .
.
4. 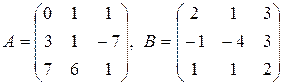 .
.
5. 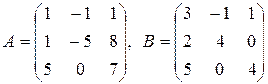 .
.
6.  .
.
7.  .
.
8.  .
.
9.  .
.
10.  .
.
11. 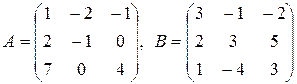 .
.
12.  .
.
13.  .
.
14.  .
.
15.  .
.
16.  .
.
17.  .
.
18.  .
.
19.  .
.
20.  .
.
21.  .
.
22.  .
.
23. 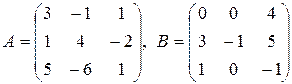 .
.
24. 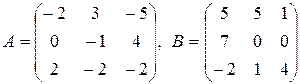 .
.
25.  .
.
26.  .
.
27.  .
.
28.  .
.
29. 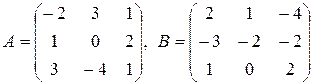 .
.
30. 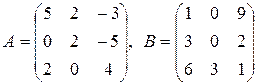 .
.
31.  .
.
32. 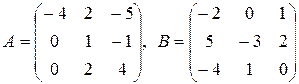 .
.
33.  .
.
34.  .
.
35. 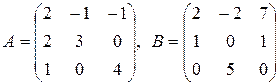 .
.
2. Обчислити визначник трьома способами:
а) за означенням (правило трикутника);
б) розклавши визначник за елементами рядка або стовпчика;
в) звівши за допомогою властивостей до трикутного вигляду.
1. 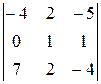 . 2.
. 2. 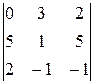 . 3.
. 3. 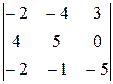 .
.
4.  . 5.
. 5. 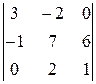 . 6.
. 6.  .
.
7.  . 8.
. 8.  . 9.
. 9.  .
.
10.  . 11.
. 11.  . 12.
. 12.  .
.
13.  . 14.
. 14.  . 15.
. 15.  .
.
16.  . 17.
. 17. 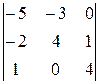 . 18.
. 18.  .
.
19.  . 20.
. 20.  . 21.
. 21.  .
.
22.  . 23.
. 23.  . 24.
. 24.  .
.
25. 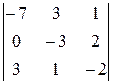 . 26.
. 26. 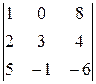 . 27.
. 27. 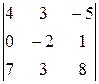 .
.
28.  . 29.
. 29.  . 30.
. 30. 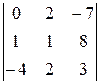 .
.
31.  . 32.
. 32. 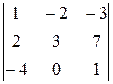 . 33.
. 33.  .
.
34.  . 35.
. 35. 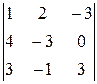 .
.
3. Розв’язати систему: а) матричним способом; б) за формулами Крамера; в) методом Гауса.
1. 
2. 
3. 
4. 
5. 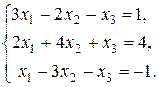
6. 
7. 
8. 
9. 
10. 
11. 
12. 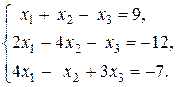
13. 
14. 
15. 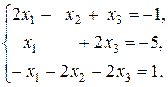
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 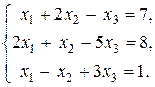
26. 
27. 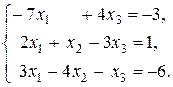
28. 
29. 
30. 
31. 
32. 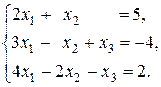
33. 
34. 
35. 
4. Дослідити систему лінійних рівнянь на сумісність. У випадку сумісності розв’язати її.
1.  2.
2. 
3.  4.
4. 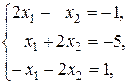
5.  6.
6. 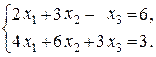
7.  8.
8. 
9.  10.
10. 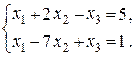
11. 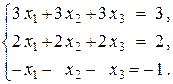 12.
12. 
13.  14.
14. 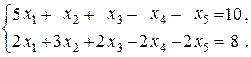
15.  16.
16. 
17.  18.
18. 
19.  20.
20. 
21.  22.
22. 
23. 24.
24. 
25.  26.
26. 
27.  28.
28. 
29. 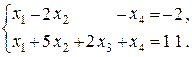 30.
30. 
31.  32.
32. 
33.  34.
34. 
35. 
5. В базисі  дано вектори
дано вектори 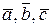 . Показати, що вектори
. Показати, що вектори 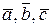 утворюють базис, і знайти координати вектора
утворюють базис, і знайти координати вектора 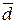 в базисі
в базисі 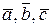 .
.
1. 
2. 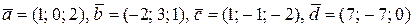
3. 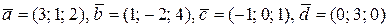
4. 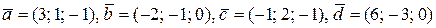
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 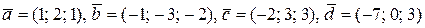
14. 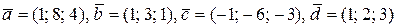
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 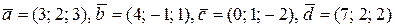
29. 
30. 
31. 
32. 
33. 
34. 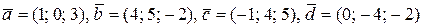
35.  .
.
6. Задано вершини піраміди 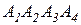 . За допомогою засобів векторної алгебри знайти:
. За допомогою засобів векторної алгебри знайти:
1) довжину ребра  ;
;
2) кут між ребрами  і
і ;
;
3) площу грані  ;
;
4) проекцію вектора  на вектор
на вектор 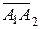 ;
;
5) об’єм піраміди 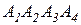 .
.
| 1. | A1( 1, –1, 0) | A2( 3, -2, -3) | A3( -2 , 1, 4) | A4( 1, 5, 8) |
| 2. | A1( 0, 4, -4) | A2( 5, 1, -1) | A3( -1, -1, 3) | A4( 0, -3, 7) |
| 3. | A1( 7, 7, -5) | A2( 3, 3, -3) | A3( 5, 14, -13) | A4( 3, 5, -2) |
| 4. | A1( 1, -2, -3) | A2( 5, -2, 1) | A3( 2, 1, -4) | A4( 1, -2, 3) |
| 5. | A1( 0, 3, -4) | A2( -1, -3, 4) | A3( 2, -1, 3) | A4( -5, 1, 1) |
| 6. | A1( 8, 0, 1) | A2( 2, 2, 3) | A3( -5, 3, 2) | A4( 4, -4, 0) |
| 7. | A1( -6, 4, 2) | A2( -3, -4, 0) | A3( 0, -1, 2) | A4( -3, 0, 3) |
| 8. | A1( -1, 5, -8) | A2( 1, -2, 0) | A3( -3, -4, 3) | A4( -3, -6, 2) |
| 9. | A1( 1, 12, -15) | A2( -1, 1, -5) | A3( -1, 3, -4) | A4( 3, 5, -7) |
| 10. | A1( 12, -2, 10) | A2( 9, 0, 8) | A3(1, -4, 0) | A4( 2, -6, 2) |
| 11. | A1( 10, 0, 2) | A2( 7, 2, 0) | A3( -1, -2, -8) | A4( 0, -4, -6) |
| 12. | A1( -8, 3, -1) | A2( 3, 5, 9) | A3( -7, 1, 1) | A4( 0, 7, 7) |
| 13. | A1( 13, 1, 6) | A2( 10, 3, 4) | A3( 2, -1, -4) | A4( 3, -3, -2) |
| 14. | A1( 3, 1, -2) | A2( 4, -2, 0) | A3( 11, 5, 6) | A4( 14, 3, 8) |
| 15. | A1( 1, 0, -8) | A2( 0, 2, 8) | A3( -10, 6, -2) | A4( 11, 4, 0) |
| 16. | A1( 4, 0, 6) | A2( 6, 9, -5) | A3( 8, 2, 3) | A4( 4, -2, 5) |
| 17. | A1( 6, 1, 10) | A2( -1, -5, 4) | A3( 9, -1, 12) | A4( -2, -3, 2) |
| 18. | A1( -4, 5, -5) | A2( 4, 5, 3) | A3( 7, 7, 5) | A4( -3, 3, -3) |
| 19. | A1( -7, 1, 1) | A2( 0, 7, 7) | A3( -8, 3, -1) | A4( 3, 5, 9) |
| 20. | A1( 6, 1, -1) | A2( 2, -3, 1) | A3( 2, -1, 2) | A4( 4, 8, -9) |
| 21. | A1( -3, 4, -3) | A2( -2, 2, -1) | A3( 8, 6, -7) | A4( 5, 8, 5) |
| 22. | A1( -1, -5, 4) | A2( 9, -1, 12) | A3( 6, 1, 10) | A4( -2, -3, 2) |
| 23. | A1( 3, 5, -7) | A2( -1, 1, -5) | A3( -1, 3, -4) | A4( 1, 12, -15) |
| 24. | A1( -4, 2, -1) | A2( 0, 6, -3) | A3( -2, -13, 11) | A4( -4, 4, 0) |
| 25. | A1( -5, 1, 1) | A2( 0, 3, -4) | A3( -1, -3, 4) | A4( 2, -1, 3) |
| 26. | A1( 1, 4, -1) | A2( 4, -1, 2) | A3( 1, -8, 8) | A4( 5, 3, 2) |
| 27. | A1( 4, 2, -1) | A2( 2, -1, 4) | A3( -2, 3, 4) | A4( -1, -1, 1) |
| 28. | A1( 7, 7, -5) | A2 ( 3, 3, -3) | A3( 3, 5, -2) | A4( 5, 14, -13) |
| 29. | A1( -1, 4, -4) | A2( 5, 0, -1) | A3( -4, -1, 3) | A4 ( 0, -3, 6) |
| 30. | A1( 0, 7, -2) | A2( -2, 9, -10) | A3( -3, 4, 0) | A4( -6, 2, -1) |
| 31. | A1( 2, 6, -3) | A2( 1, 3, -1) | A3( -8, 4, 0) | A4( -5, -2, 1) |
| 32. | A1( 0, 5, -3) | A2( -2, 1, -4) | A3( -4, -7, 1) | A4( 3, -1, 7) |
| 33. | A1( 1, 7, 0) | A2( -1, 5, -9) | A3( 4, 4, 8) | A4( -3, 2, -1) |
| 34. | A1( 0, 2, -4) | A2( 1, 10, -8) | A3( -2, -2, 0) | A4( 5, 7, -1) |
| 35. | A1( -3, 0, -3) | A2( -2, 4, -11) | A3( 8, -4, 0) | A4( -7, -2, 6) |
7. Дано вершини трикутника 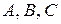 . Знайти:
. Знайти:
а) рівняння сторони 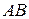 ; б) рівняння та довжину висоти
; б) рівняння та довжину висоти 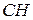 ;
;
в) рівняння та довжину медіани 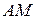 ; г) точку
; г) точку  перетину висоти
перетину висоти 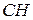 і медіани
і медіани 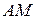 ; д) рівняння прямої, що проходить через точку
; д) рівняння прямої, що проходить через точку  паралельно стороні
паралельно стороні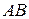 .
.
1.  . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
7.  . 8.
. 8.  .
.
9. 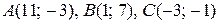 . 10.
. 10.  .
.
11.  . 12.
. 12.  .
.
13.  . 14.
. 14.  .
.
15.  . 16.
. 16. 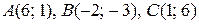 .
.
17. 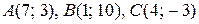 . 18.
. 18.  .
.
19.  . 20.
. 20.  .
.
21.  . 22.
. 22.  .
.
23.  . 24.
. 24.  .
.
25. 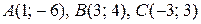 . 26.
. 26.  .
.
27. 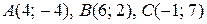 . 28.
. 28.  .
.
29.  . 30.
. 30.  .
.
31.  . 32.
. 32.  .
.
33.  . 34.
. 34.  .
.
35.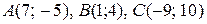 .
.
8. Дано чотири точки  ,
,  ,
, 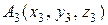 ,
,  . Знайти: а) рівняння прямої
. Знайти: а) рівняння прямої 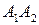 ; б) рівняння прямої
; б) рівняння прямої  , паралельної до прямої
, паралельної до прямої 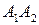 ; в) рівняння площини, що проходить через точку
; в) рівняння площини, що проходить через точку 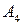 перпендикулярно до прямої
перпендикулярно до прямої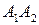 ; г) рівняння площини
; г) рівняння площини 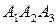 ; д) рівняння прямої
; д) рівняння прямої  перпендикулярної до площини
перпендикулярної до площини 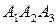 та координати точки
та координати точки  їх перетину; е) відстань
їх перетину; е) відстань  від точки
від точки 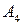 до площини
до площини 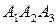 ; є) кут між прямою
; є) кут між прямою 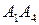 і площиною
і площиною 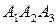 ; ж) кут між координатною площиною
; ж) кут між координатною площиною 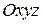 і площиною
і площиною 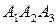 .
.
1. 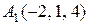 ,
, ,
,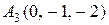 ,
, .
.
2.  ,
, ,
,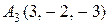 ,
, .
.
3. 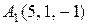 ,
,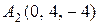 ,
, ,
, .
.
4.  ,
, ,
, ,
, .
.
5. 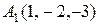 ,
, ,
, ,
, .
.
6.  ,
, ,
, ,
, .
.
7.  ,
, ,
, ,
,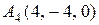 .
.
8.  ,
,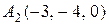 ,
, ,
,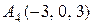 .
.
9.  ,
, ,
, ,
, .
.
10.  ,
,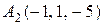 ,
, ,
, .
.
11. 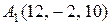 ,
, ,
, ,
, .
.
12.  ,
, ,
, ,
, .
.
13.  ,
, ,
, ,
, .
.
14.  ,
, ,
, ,
, .
.
15.  ,
,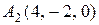 ,
, ,
, .
.
16.  ,
, ,
,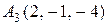 ,
, .
.
17.  ,
, ,
,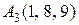 ,
, .
.
18.  ,
, ,
, ,
, .
.
19.  ,
, ,
, ,
, .
.
20.  ,
, ,
, ,
, .
.
21.  ,
, ,
,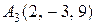 ,
, .
.
22.  ,
, ,
,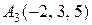 ,
, .
.
23.  ,
, ,
, ,
, .
.
24. 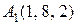 ,
, ,
, ,
, .
.
25.  ,
, ,
, ,
,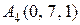 .
.
26.  ,
,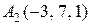 ,
,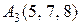 ,
, .
.
27. 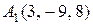 ,
, ,
, ,
,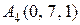 .
.
28. 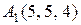 ,
, ,
,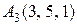 ,
, .
.
29.  ,
, ,
, ,
, .
.
30.  ,
,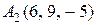 ,
, ,
,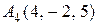 .
.
31.  ,
, ,
, ,
, .
.
32.  ,
, ,
, ,
, .
.
33.  ,
,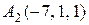 ,
, ,
, .
.
34.  ,
,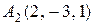 ,
,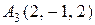 ,
, .
.
35.  ,
, ,
, ,
, .
.
9. Скласти канонічні рівняння: а) еліпса; б) гіперболи; в) параболи ( А, В – точки, що лежать на кривій, F – фокус, a –велика піввісь, b – мала піввісь,  - ексцентриситет,
- ексцентриситет,  - рівняння асимптот гіперболи,
- рівняння асимптот гіперболи,  - директриса параболи, 2с – відстань між фокусами).
- директриса параболи, 2с – відстань між фокусами).
1. а) 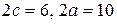 ; б)
; б) 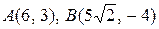 ; в)
; в)  .
.
2. а)  ; б)
; б) 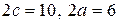 ; в) вісь симетрії
; в) вісь симетрії  .
.
3. а) 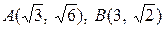 ; б)
; б) 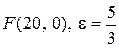 ; в)
; в)  .
.
4. а) 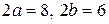 ; б)
; б)  ; в) вісь симетрії
; в) вісь симетрії  .
.
5. а)  ; б)
; б)  ; вісь симетрії
; вісь симетрії  .
.
6. а) 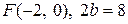 ; б)
; б)  ; в)
; в)  .
.
7. а)  ; б)
; б)  ; в)
; в)  .
.
8. а)  ; б)
; б) 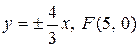 ; в) вісь симетрії
; в) вісь симетрії  .
.
9. а) 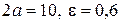 ; б)
; б)  ; в)
; в)  .
.
10. а)  ; б)
; б)  ; в)
; в)  .
.
11. а) 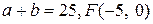 ; б)
; б) 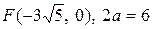 ; в) вісь симетрії
; в) вісь симетрії  .
.
12. а)  ; б)
; б) 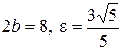 ; в)
; в)  .
.
13. а)  ; б)
; б) 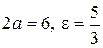 ; в) вісь симетрії
; в) вісь симетрії  .
.
14. а)  ; б)
; б)  ; в)
; в)  .
.
15. а)  ; б)
; б)  ; в)
; в) 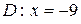 .
.
16. а)  ; б)
; б)  ; в) вісь симетрії
; в) вісь симетрії  .
.
17. а)  ; б)
; б)  ; в)
; в)  .
.
18. а) 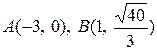 ; б)
; б)  ; в)
; в)  .
.
19. а)  ; б)
; б)  ; в) вісь симетрії
; в) вісь симетрії  .
.
20. а)  ; б)
; б)  ; в)
; в)  .
.
21. а)  ; б)
; б) 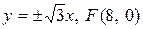 ; в) вісь симетрії
; в) вісь симетрії  .
.
22. а)  ; б)
; б)  ; в)
; в) 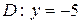 .
.
23. а)  ; б)
; б) 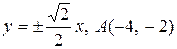 ; в)
; в)  .
.
24. а) 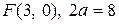 ; б)
; б) 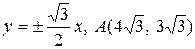 ; в)
; в)  .
.
25. а)  ; б)
; б)  ; в) вісь симетрії
; в) вісь симетрії  .
.
26. а) 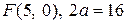 ; б)
; б) 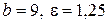 ; в) вісь симетрії
; в) вісь симетрії  .
.
27. а)  ; б)
; б) 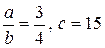 ; в)
; в)  .
.
28. а)  ; б)
; б)  ; в) вісь симетрії
; в) вісь симетрії 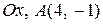 .
.
29. а) 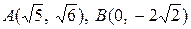 ; б)
; б) 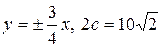 ; в)
; в) 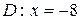 .
.
30. а) 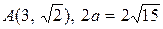 ; б)
; б) 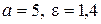 ; в)
; в) 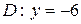 .
.
31. а)  ; б)
; б) 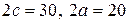 ; в)
; в) 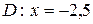 .
.
32. а)  ; б)
; б)  ; в)
; в)  .
.
33. а)  ; б)
; б)  ; в)
; в)  .
.
34. а) 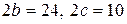 ; б)
; б) 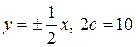 ; в) вісь симетрії
; в) вісь симетрії  .
.
35. а)  ; б)
; б) 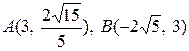 ; в) вісь симетрії
; в) вісь симетрії 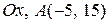 .
.
Читайте також:
- V. Завдання.
- VІ. Підсумки уроку і повідомлення домашнього завдання.
- Адаптація персоналу: цілі та завдання. Введення у посаду
- Адвокатура в Україні: основні завдання і функції
- АКТУАЛЬНI ПРОБЛЕМИ І ЗАВДАННЯ КУРСУ РОЗМIЩЕННЯ ПРОДУКТИВНИХ СИЛ УКРАЇНИ
- Актуальність і завдання курсу безпека життєдіяльності. 1.1. Проблема безпеки людини в сучасних умовах.
- Аналіз руху грошових коштів у контексті нової фінансової звітності Важливим завданням аналізу фінансового стану підприємства є оцінка руху грошових коштів підприємства.
- Аудит, його мета та завдання
- Багатокритеріальні завдання оптимального керування
- Багатокритерійні завдання і можливі шляхи їхнього рішення.
- Безпека життєдіяльності людини – найважливіше завдання людської цивілізації
- Бухгалтерська звітність, її значення, завдання і вимоги
| <== попередня сторінка | | | наступна сторінка ==> |
| ВІДПОВІДІ | | | Тестові завдання з лінійної алгебри |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |