• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Графічний спосіб задання множин

(спосіб задання множин кругами Ейлера).

При заданні множин кругами Ейлера універсум подається у вигляді прямокутника, а сама множина А у вигляді круга. Множини і підмножини штрихуються.

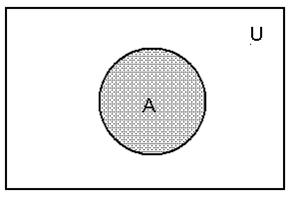
Рис.1. Множина А.

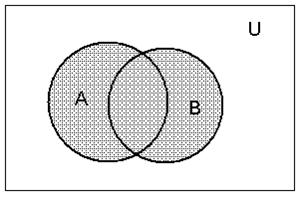
Рис. 2. Об’єднання множин

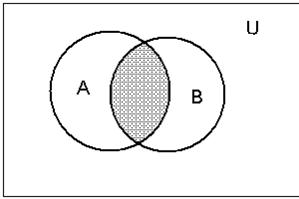
Рис.3.Перетин множин

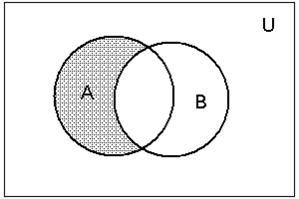
Рис. 4. Різниця множин

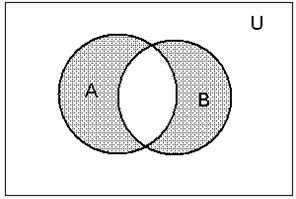
Рис. 5. Диз’юнктивна сума

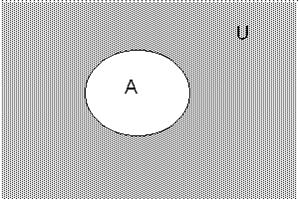
Рис. 6. Абсолютне Доповнення А ()

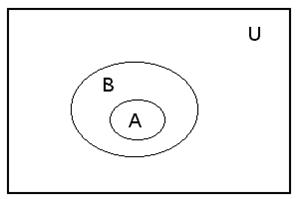
Рис. 7. А підмножина В

Тотожні перетворення. Алгебра множин представляє собою теоретико-множинний аналог звичайної алгебра дійсних чисел та основана на властивостях операцій над множинами. Один з розділів алгебри множин є тотожні перетворення за допомогою яких можливоспрощувати або приводити до зручного виду різні вирази, які містять множини.

Приклад

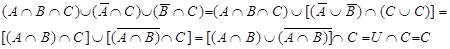
Рівняння з множинами. Алгебра множин розглядає рівняння, які містять фіксовані підмножини А₁, А₂,..., А_n, та підлягаючі визначенню підмножини Х₁, Х₂, ..., Х_n. В простому випадку у рівняння входить одна така підмножина Х. Необхідно дати відповідь на питання, при яких умовах рівняння має рішення і, якщо ці умови витримуються, знайти усі рішення, тобто визначити Х.

Рішення рівняння з однією підмножиною Х, грунтується на послідовності тотожних перетворень:

1. У відповідності з властивостями(табл.1) рівність перетворюється у диз’юнктивну суму його лівої та правої частини, дорівнює порожній множині.

2. Отримане рівняння перетворюється до виду , де М і N - деякі множини, які не містять Х .

3. Так як об’єднання множин порожнє тільки при умові, що кожне з них також порожня множина, перетворене рівняння запишемо залежною системою двох рівнянь:

М ÇX = Æ i NÇ.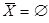

4. Пара рівнянь має значення тоді і тільки тоді, коли N Ì X i X Ì . Це означає, що умовою існування рішення є 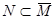(властивість транзитивності відношення включення), а рішенням рівняння - будь-яка множина Х така, що N Ì X Ì .

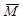Приклад: X È C = D.

1) (X È C) + D = Æ.

2)

Читайте також:

1. I спосіб.
2. Адміністративно-правовий спосіб захисту прав
3. Адміністративно-правовий спосіб захисту прав
4. Алгебра множин
5. Алгебраїчний спосіб визначення точки беззбитковості
6. Аналогія - спосіб отримання знань про предмети та явища на основі їхньої подібності з іншими.
7. Атракція як спосіб викликати довіру до реклами
8. Бюджетний устрійпоказує, в який спосіб побудована бюджетна система. Іншими словами,він відображає організацію вертикальної структури бюджету держави за рівнями влади.
9. Бюджетні множини й лінії бюджетного обмеження
10. Визначення добутку на множині цілих невід’ємних чисел, його існування та єдиність. Операція множення та її основні властивості (закони).
11. Визначення множини допустимих планів задачі ЛП
12. Визначення суми на множині цілих невід’ємних чисел, її існування та єдиність. Операція додавання та її основні властивості (закони).

Переглядів: 2307