• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Тема 2. Множини, відношення, функції, операції

Завдання моделювання

1. Задача аналізу – знайти функціональні залежності між станом, вхідними, вихідними, керованими і некерованими змінними

Y = F(S, X, x)

2. Задача оптимізації – знаходження екстремуму

extr Y = F(S*, X, x)

3. Задача оптимального управління – знайти екстремальне значення вихідних параметрів, коли фіксований стан, а впливати можемо на вхідні дії.

extr Y = F(S,X*, x)

Класифікація математичних моделей за ознаками;

1. Поведінка моделей в часі :

- динамічні;

- статистичні;

- квазістатичні.

Динамічні – математичні моделі об’єктів, параметри яких змінюються у часі. Змінюється в часі стан системи ,його параметри і характеристики.

Статичні – математичні моделі для яких параметри або стан є фіксовані.

Квазістатичні – в результаті розподілу динамічних задач на статичні.

Параметри на окремому проміжку часу не змінюються.

2. Залежить від обсягу інформації про параметри і змінні:

- детерміновані моделі;

- стохастичні моделі;

Детермінована модель – математична модель, коли відомі конкретні значення параметрів( з певною точністю).

Стохастичні – для аналізу стохастичних моделей коли невідомі точні значення параметрів, а відома тільки ймовірність цих значень (використовують теорію ймовірності).

3. За характером операцій, з врахуванням взаємодії факторів моделі:

- лінійні

- нелінійні.

4. За типом математичних алгоритмів:

- рівняння і нерівності (алгебраїчні, диференційні, інтегральні, комбіновані)

Алгебраїчні рівняння – в яких змінна входить в математичний вираз в певній степені і використовуються математичні оператори ( сума, ділення, відношення, добуток)

Диференційні рівняння – в яких використовуються не лише значення функцій і аргументів, а й похідні.

Інтегральні рівняння - в яких використовуються крім функцій і аргументів ще й інтеграли цих функцій.

Для моделювання дискретних систем використовуються:

- теорія графів;

- алгебру логіки;

- теорія автоматів;

- математичне програмування.

Для моделювання стохастичних систем використовують:

- теорія ймовірностей;

- математична статистика;

- теорія планування експерименту;

- теорія ігор;

- задачі масового обслуговування.

Для моделювання інформаційних процесів використовують:

- математичний апарат теорії інформації.

Поняття множини - одне з основних понять математики. Воно не має точного означення, і його слід віднести до аксіоматичних понять.

Множина - сукупність елементів, що мають певні властивості і знаходяться в деяких відношеннях між собою або з елементами інших множин.

Відношення - будь-який зв’язок між предметами або поняттями, тобто елементами множини.

Множина - важливе поняття, як об’єднання елементів в єдине ціле.

Множина, до складу якої входить скінчена кількість елементів називається скінченою.

Множина, до складу якої входить нескінченна кількість елементів називається нескінченною.

Характеристики скінченої множини:

-множина, яка містить тільки один елемент називається одиничною множиною;

-множина, яка не містить елементів, називається порожньою множиною. Вона відіграє ту ж саму функцію, як і «Æ» в алгебрі та арифметиці.

Способи задання множин

I. Скінченні множини задаються переліком своїх елементів.

Множина позначається великою латинською літерою (чи інших алфавітів).Елементи множин позначаються малою літерою.

A={a, b, c, d} - це різні об’єкти, різні предмети, яким відповідають ці літери.

íý - позначають множину.

Щоб показати належність до множини, вводиться відношення належності - “Δ:

aÎA; bÎB; fÏА;

«É»- виключає: A É a; A É b; A Ë f .

Найчастіше для скінчених множин, які мають об’єкти однієї природи вводять позначення і множини, і елементів однією і тією ж самою літерою. Тоді елементи відрізняються за індексами:

X={x₁, x₂, x₃, x₄, x₅}

наприклад X - множина країн Європи.

Для узагальнення , часто, коли потрібно подати, що в множині є n елементів записують:

X={x₁, x₂, x₃, x₄,...., x_n}.

II. Множини можуть задаватися: через вказання властивостей, якими володіють елементи множини:

X={x_i /p(x)} - це множина елементів x_i, які володіють властивостями P(x)

тобто функція, висловлювання.

Наприклад:

У={у_і / держави Балтії}

Множина А, всі елементи якої належать і множині В, називається підмножиною множини В.

Це відношення між множинами А і В називається включенням підмножини:

А={a,b,c}

B={a,b,c,d,e,f}

Множина А є підмножиною множини В (рис.7).

А Ì В - включення підмножини, BÉA-множина В включає підмножину А.

А={a, b, c} Множини А і С тотожні

С ={c, a, b} А = С (рівні)

Множина А є підмножиною С, а множина С є підмножиною А.

А Ê С, С Í А

Будь-яка не порожня множина А має щонайменше 2-ві підмножини: тотожну їй і порожню множини ( АÊА , АÉ{Æ} ). Порожня множина не містить елементів. Отже, додаючи до множини А порожню множину, ми фактично нічого не додаємо. Тому завжди можна вважати, що будь-яка множина А містить порожню множину як підмножину.

Універсум U. Сукупність допустимих об’єктів зафіксувати явно та вважати, що множини, які розглядаються, складаються х елементів цієї сукупності. Її називають основною множиною (універсумом) і позначається “U ”.

Універсум U арифметики - числа, універсум U міжнародних відносин - країни і т.д.

Будь-яку множину розглядатимемо у зв’язку з універсумом, який на колах Ейлера асоціюватимемо з прямокутником на площині, всередині якого зображатимемо множини.

Нова операція U - A = (абсолютне доповнення А) - це множина, що містить усі елементи універсуму, за винятком елементів А (рис.6).

Операції над множинами.

Введемо символи Û, $x, "x, Þ,які надалі будуть служити для скорочення виразів «тоді і тільки тоді, коли», «існує х такий, що», «для всякого х» і «слідує» або «випливає» відповідно.

1. Об’єднання множин

Об’єднанням множин А і В є множина С, елементи якої належать або множині А, або множині В.

Операція об’єднання позначається ”È, В={b, c, d, l}, А ={a, b, c}, з відси

C=AÈB={a, b, c, d , l}.

 

2. Перетином множин А і В є така множина С, елементи якої належать одночасно і А і В. Перетин позначається “Ç”, С = АÇВ = {b, c}.

Множини, які не мають спільних елементів називаються неперетинними D={f, k} Þ DÇA={Æ}.

 

3. Різниця множин

Різницею множин А і В є множина С, елементи якої складаються з усіх А, які не входять до В. Позначається “\” або ”-”

С=А\В={a} або C=A-B={a}. Якщо С=В\А={d, l}.

 

4. Диз’юнктивна сума.

Диз’юнктивна сума множин А і В є множина С, елементи якої належать або множині А, або множині В, але не обом разом. Позначається «+», «Å»

C=AÅB={a,, d, e}.

 

5. Декартовий добуток.

Декартовий добуток множин А і В - множина С, яка складається з двоелементних підмножин, в яких 1-й елемент належить множині А, а 2-й –належить множині В. Позначається - “х” або “Ä”

 

C=AÄB=í{a,b},{a,c},{a,d},{a,e},{b,b},{b,c},{b,d},{b,c},{c,c},{c,d},{c,e}ý.

Властивості операцій над множинами.

Таблиця 1

Об’єднання	Перетин
Комутативний закон
AÈB=BÈA	AÇB=BÇA
Асоціативний закон
AÈBÈC=(AÈB)ÈC==AÈ(BÈC)= BÈ(AÈC)	AÇBÇC=(AÇB)ÇC==AÇ(BÇC)= BÇ(AÇC)
Дистрибутивний (розподільчий) закон
AÈ(BÇC)= =(AÈB)Ç(AÈC)	AÇ(BÈC)= =(AÇB)È(AÇC)
Властивості Æ та U
AÈÆ = A	AÇÆ = Æ
AÈU = U	AÇU = A
AÈ=U	AÇ=Æ
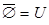
Закон ідемпотентності (самопоглинання)
А È А =А	А Ç А = А
Закон поглинання
А È (А Ç В) = А	А Ç (А È В) = А
Теорема де Моргана
=	=
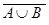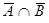
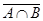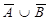
Властивості доповнення, різниці та рівності
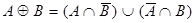A - B=A 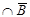A Å B=B Å A A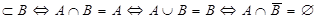 A= B Û (AÇ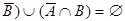

 

---

Читайте також:

1. Активні операції банків
2. Активні операції комерційних банків
3. Алгебраїчні операції
4. Арифметичні операції
5. Арифметичні операції в різних системах числення
6. Арифметичні операції над цілими числами
7. Базальні ядра, їх функції, симптоми ураження
8. Базові функції, логічні функції
9. Банк і його операції. Правова природа банківської діяльності
10. Бартерні операції
11. Біржові операції.
12. Біржові операції. Котирування цін на біржі

---

Переглядів: 1461

<== попередня сторінка	|	наступна сторінка ==>
Класифікація моделей	|	Графічний спосіб задання множин

Не знайшли потрібну інформацію? Скористайтесь пошуком google: