• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Приклад виконання задачі 11

Задача 11. Розкриття статичної невизначуваності рами

Завдання до розрахунково-графічної роботи

Для заданої статично невизначеної стальної рами (рис. 3.11) двотаврового попереречного перерізу побудувати епюри внутрішніх зусиль. Підібрати номер двотавра при = 160 МПа та визначити величину переміщень вертикального 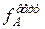, горизонтального 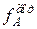або кут повороту переріза в т. А, вказаного в таблиці 3.1.

План розв’язування

1. Визначити ступінь статичної невизначуваності.

2. Вибрати основну та скласти еквівалентну систему.

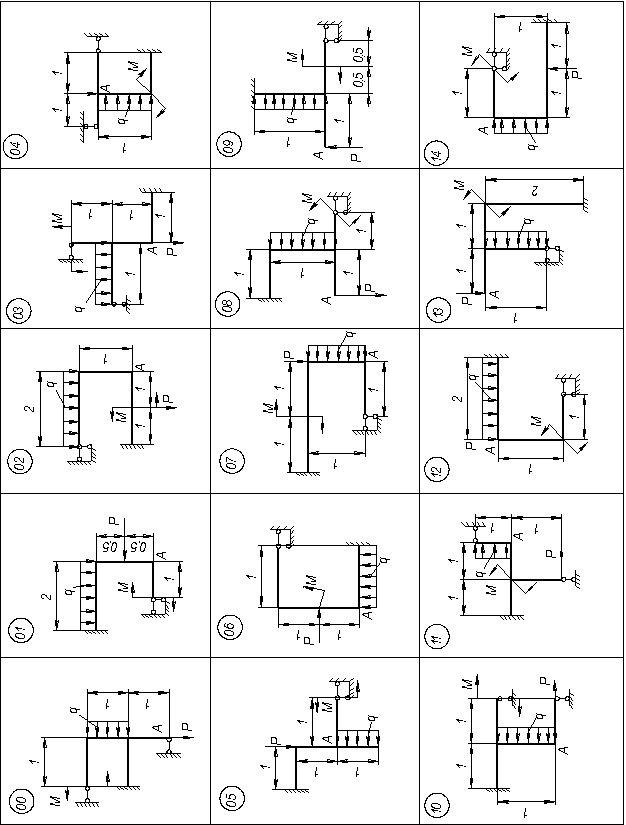
Рис. 3.11. Схеми до виконання задачі 11

3. Скласти канонічні рівняння методу сил, визначити коефіцієнти цих рівнянь та розв’язати отриману систему рівнянь.

4. Побудувати епюри поперечної, поздовжньої сили та згинального момента.

5. Виконати деформаційну перевірку правильності розкриття статичної невизначуваності.

6. Підібрати двотавровий переріз рами з умови міцності за нормальними напруженнями.

7. Визначити переміщення переріза в т. А, вказаного в таблиці 3.1.

Таблиця 3.1

№	q, кн/м	Р, кН	М, кНм	Переміщення
				*
				*
				*
				*
				*

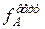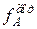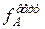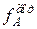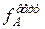*Якщо вказане переміщення дорівнює нулю (за схемою навантаження одиничною силою), то необхідно шукати інше переміщення: 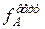або .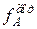

Розрахувати статично невизначену раму, зображену на рис. 3.12, а, згідно плану задачі 11.

Дано:

Р= 5 кН;

М= 15 кН*м;

q = 10 кН/м;

= 160 МПа.

Знайти:

N, Q і М_z; № перерізу; вертикальне та кутове переміщення т. С.

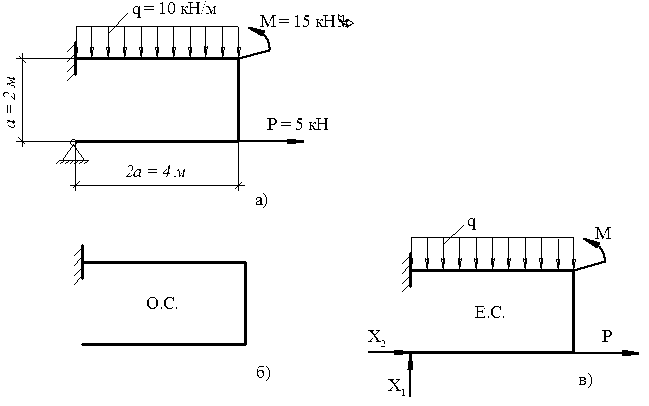
Рис. 3.12. Задана, основна і еквівалента системи

Розв’язування

1. Визначаємо ступінь статичної невизначуваності

s = 3к – ш = 3*2 – 4 = 2.

2. Вибираємо основну систему (рис. 3.12, б).

3. Будуємо еквівалентну систему (рис. 3.12, г). позначені невідомі реакції опори в т. А.

4. Запишемо систему канонічних рівнянь методу сил та визначаємо коефіцієнти канонічних рівнянь.

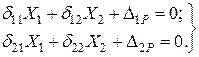
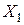4.1. Завантажуємо основну систему одиничною силою (замість невідомої в тому ж напрямку) (рис. 3.13) . Будуємо епюри згинаючого момента 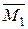від дії одиничної сили (рахуємо, що поздовжні та поперечні сили створюють набагато менші переміщення ніж згинаючий момент, тому ними будемо нехтувати).

4.2. Завантажуємо основну систему одиничною силою 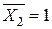. Будуємо епюри згинаючого момента 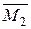для одиничного стану (рис. 3.13).

4.3. Завантажуємо основну систему зовнішнім навантаженням. Будуємо епюри згинаючого момента для вантажного стану (рис. 3.13).

4.4. Визначаємо коефіцієнти канонічних рівнянь шляхом розкриття інтегралу Мора через способи Верещагіна, Сімпсона-Карнаухова, Верещагіна-Даркова (додаток Ж). Спосіб перемноження епюр на кожній ділянці вибирається за бажанням, проте важливо пам’ятати, що спосіб Верещагіна-Даркова справедливий лише для прямолінійних епюр.

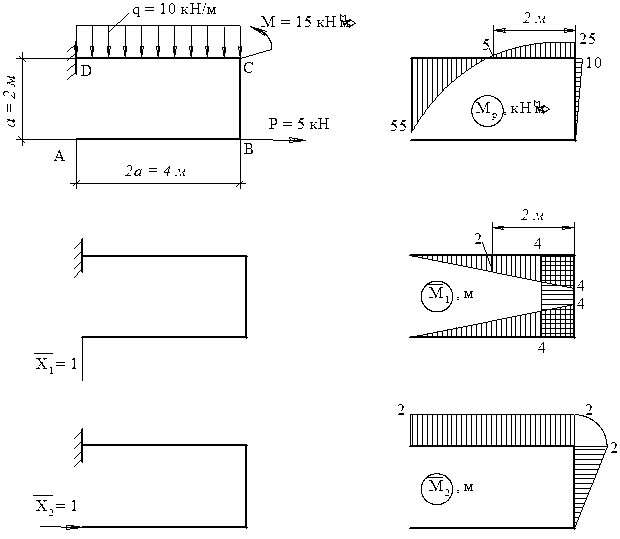
Рис. 3.13. Вантажні та одиничні епюри

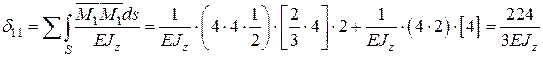
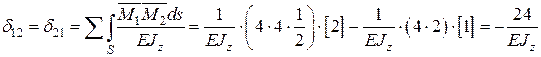
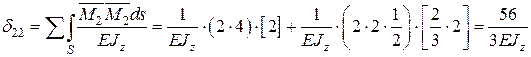
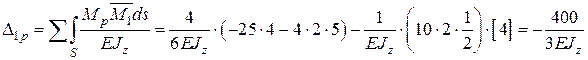
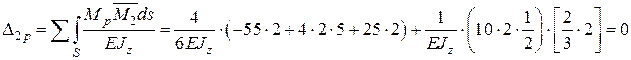4.5. Розв’язуємо систему канонічних рівнянь методу сил та визначаємо

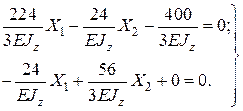
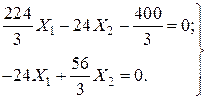або

Звідки дістаємо (шляхом стандартного розв’язання отриманої системи рівнянь)

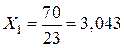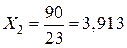(кН),

(кН).

Виконуємо перевірку розв’язку

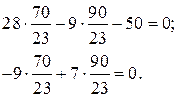
5. Розглядаємо еквівалентну систему разом із знайденими реакціями (рис. 3.14) та будуємо епюри N, Q і М_z.

6. Виконуємо перевірку розкриття статичної невизначеності (деформаційну). Кількість перевірок має бути рівною ступені статичної невизначеності.

Вибираємо основну систему, відмінну від попередньої і визначаємо переміщення точок, які за умовою задачі дорівнюють „0”. Зокрема, вертикальне та кутове переміщення перерізу в точці D (рис. 4).

6.1. Завантажуємо основну систему одиничною силою 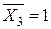. Знаходимо необхідні реакції. Будуємо епюри згинаючого момента 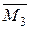для одиничного стану (рис. 4).

Вертикальне переміщення перерізу в точці D

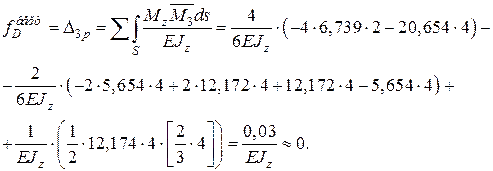
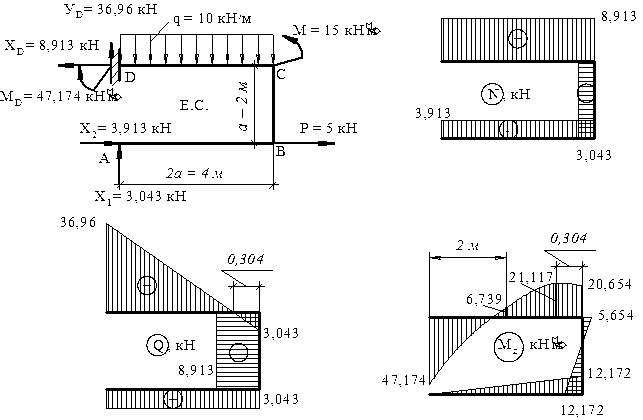
Рис. 3.14. Епюри внутрішніх зусиль

6.2. Завантажуємо основну систему одиничним моментом 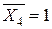. Знаходимо необхідні реакції. Будуємо епюри згинаючого момента 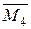для одиничного стану (рис. 3.15).

Кутове переміщення перерізу в точці D

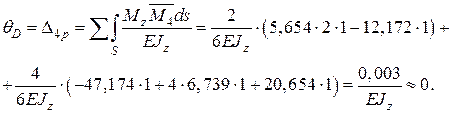
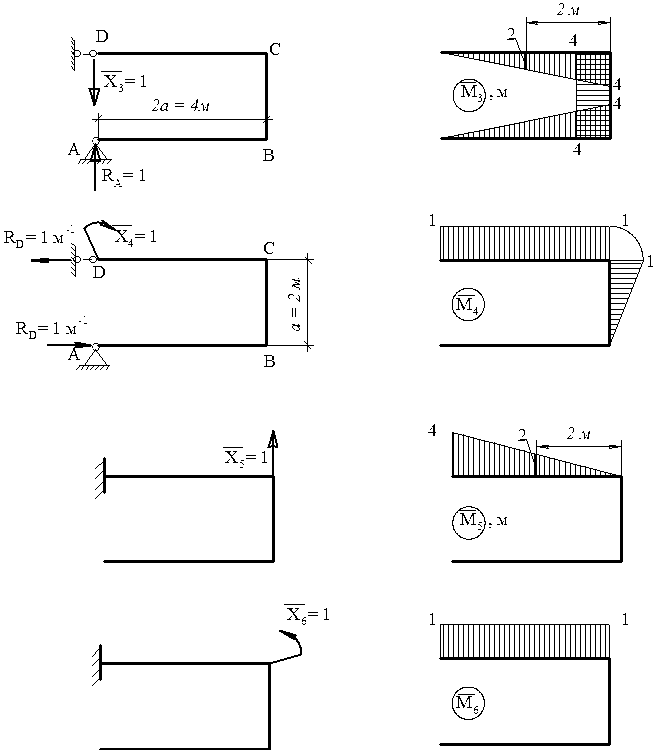
Рис. 3.15. Одиничні епюри

Оскільки знайдені переміщення близькі до нуля (через округлення розрахункових величин), то робимо висновок, що статична невизначеність розкрита правильно.

7. Підбираємо переріз за умови міцності.

Поперечними та поздовжніми силами нехтуємо.

Умова міцності

.

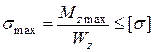Необхідний момент опору

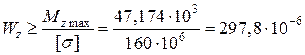(м³) = 297,8 см³.

За сортаментом підбираємо двотавр №24а (додаток В), для якого см³, І_z = 3800 см⁴.

8. Визначаємо вертикальне та кутове переміщення т. С.

8.1. Завантажуємо основну систему (можна будь-яку, проте простіше працювати з консольною рамою при побудові епюр) одиничною силою 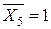. Будуємо епюри згинаючого момента 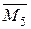для одиничного стану (рис. 3.15).

Вертикальне переміщення перерізу в точці С

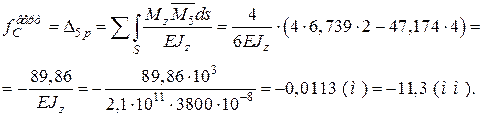
Знак мінус показує, що переріз переміщується вниз (проти напрямку одиничної сили ).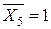

8.2. Завантажуємо основну систему одиничним моментом 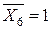. Будуємо епюри згинаючого момента 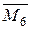для одиничного стану (рис. 3.15).

Кутове переміщення перерізу в точці С

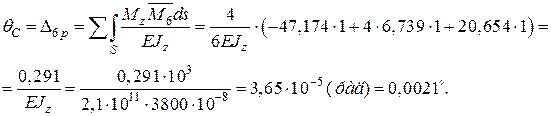
Отриманий кут повороту близький до нуля.

Відповідь: двотавр №24а, 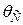= 0,0021⁰ »0, 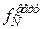= 11,3 мм.

Питання до захисту розрахунково-графічної роботи (задача 11)

1. Записати систему канонічних рівнянь для один раз та двічі статично невизначеної системи.

2. Як визначити ступінь статичної невизначеності рами?

3. Що називається основною системою? Нарисувати принаймні дві основних системи для заданої.

4. Що називається еквівалентною системою?

5. Що називається вантажним станом при розкритті статичної невизначеності системи?

6. Як визначаються коефіцієнти канонічних рівнянь методу сил? Показати на прикладі.

7. За яким алгоритмом розкривають статичну невизначеність рами?

8. За яким алгоритмом визначаються переміщення перерізу в статично невизначеній рамі?

9. В чому полягає зміст деформаційної перевірки розкриття статичної невизначуваності?

4 СТІЙКІСТЬ СТИСНУТИХ СТРИЖНІВ (buckling)

Читайте також:

1. III. Виконання бюджету
2. III. Вимоги безпеки під час виконання роботи
3. III. Вимоги безпеки під час виконання роботи
4. V. Виконання вправ на застосування узагальнювальних правил.
5. Абсолютні синоніми (наприклад, власне мовні й запозичені) в одному тексті ділового стилю вживати не рекомендується.
6. Алгоритм однофакторного дисперсійного аналізу за Фішером. Приклад
7. Алгоритм розв’язання задачі
8. Алгоритм розв’язання розподільної задачі
9. Алгоритм розв’язування задачі
10. Алгоритм розв’язування задачі
11. Алгоритм розв’язування задачі
12. Алгоритм розв’язування задачі

Переглядів: 1931