Формула Ейлера для визначення критичної сили стиснутого стрижня

Стійка та нестійка пружна рівновага

Короткі теоретичні відомості

Виконуючи розрахунки на міцність та жорсткість при різних деформаціях, ми вважали, що під час деформації будь-якої системи має місце лише одна наперед відома форма рівноваги. Насправді у деформованому стані рівновага між зовнішніми та спричиненими ними внутрішніми силами пружності може бути не тільки стійкою, а й нестійкою.

Пружна рівновага буде стійкою, якщо деформоване тіло при будь-якому малому відхиленні від стану рівноваги намагається повернутися до початкового стану й повертається до нього після припинення зовнішнього впливу, який порушив початковий стан рівноваги.

Пружна рівновага нестійка, якщо деформоване тіло, виведене з неї будь-якою зовнішньою дією, продовжує деформуватися в напрямі наданого йому відхилення й після припинення зовнішньої дії у вихідний стан не повертається.

Між цими двома станами рівноваги існує перехідний стан, який зветься критичним, при якому деформоване тіло перебуває у байдужій рівновазі: воно може зберегти вихідну форму, але може й втратити її внаслідок навіть дуже незначного впливу.

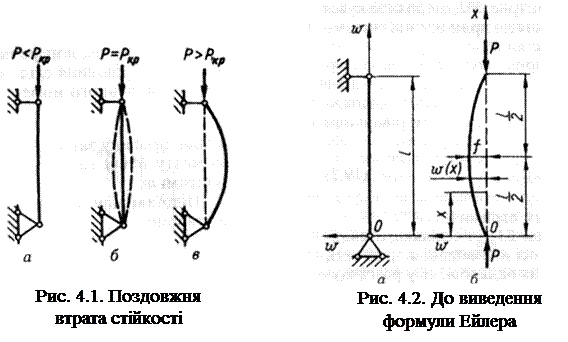
Стійкість форми рівноваги деформованого тіла залежить від прикладених до нього навантажень. Наприклад, якщо сили, що стискають стрижень, невеликі, то вихідна форма рівноваги залишається стійкою (рис. 4.1, а). При зростанні прикладених сил досягається стан байдужої рівноваги, при якому поряд з прямолінійною формою стрижня можливі суміжні з нею злегка викривлені форми рівноваги (штрихові лінії на рис. 4.1, б). При дальшому найнезначнішому збільшенні навантаження характер деформації стрижня різко змінюється – стрижень випинається (рис. 4.1, в), прямолінійна форма рівноваги перестає бути стійкою. Це означає, що навантаження перевищило критичне значення.

Навантаження, перевищення якого спричинює втрату стійкості вихідної форми тіла, називають критичним і позначають Р_кр (critical load).

Можна стверджувати, що досягнення навантаженнями критичних значень рівнозначне руйнуванню конструкції, оскільки нестійка форма рівноваги неминуче буде втрачена, що пов'язано з практично необмеженим зростанням деформацій та напружень. Особлива небезпека руйнування внаслідок втрати стійкості полягає в тому, що, як правило, воно відбувається раптово й при низьких значеннях напружень, коли міцність елемента ще далеко не вичерпана.

До моменту настання критичного стану пружні деформації за модулем зовсім невеликі, і зростання їх майже непомітне для ока. Проте з моменту настання критичного стану до моменту руйнування залишкові деформації наростають надто швидко, й практично немає часу вжити заходів щодо запобігання катастрофі, яка загрожує. Отже, при розрахунку на стійкість критичне навантаження подібне руйнувальному при розрахунку на міцність. Для забезпечення певного запасу стійкості необхідно, щоб задовольнялася умова

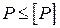. (4.1)

Тут

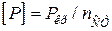. (4.2)

де Р – діюче навантаження; n_ст – коефіцієнт запасу стійкості.

Отже, щоб розрахувати стиснуті стрижні на стійкість, треба вивчити способи визначення критичних навантажень Р_кр.

Припустимо, що під дією сили Р, яка дещо перевищує критичну силу Р_кр, стрижень з шарнірно закріпленими кінцями (рис. 4.2, а) трохи зігнувся (рис. 4.2, б).

Найменше значення поздовжньої стискальної критичної сили (Euler load) Р_кр, при якому стає можливим поздовжнє згинання

. (4.3)

Рівняння (4.3) є формулою, що вперше була виведена Ейлером.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Приклад виконання задачі 11	\|	Поняття про втрату стійкості при напруженнях, що перевищують границю пропорційності

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.