Властивості середньої арифметичної

Середня арифметична має певні математичні властивості:

1. Якщо кожну варіанту зменшити або збільшити на будь яку постійну величину А, то середня зменшити або збільшити відповідно на ту саму величину;

Покажемо цю властивість середньої арифметичної на прикладі, припустимо що А=54.

Денний виробіток ткачих, м (x)	Кількість ткачих (f)	Загальний виробіток ткачих, м (xf)	Розрахунок середньої при зменшенні варіанти на число А	Розрахунок середньої при збільшенні варіанти на число А
x-А	(x-А)f	x+А	(x+А)f

			-8 -4 +4	-560 -680 +240
Всього			-	-1000	-

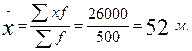
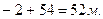
2. Якщо кожну варіанту розділити чи помножити на будь яку постійну величину А, то середня зменшиться або збільшиться в стільки ж разів;

Покажемо цю властивість середньої арифметичної на прикладі, припустимо що А=2.

Денний виробіток ткачих, м (x)	Кількість ткачих (f)	Розрахунок середньої при зменшенні варіанти на число А	Розрахунок середньої при збільшенні варіанти на число А
х/А	(x/А)f	X*А	(x*А)f


Всього		-		-

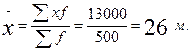
3. Якщо частоту кожної з груп зменшити або збільшити в одне й те саме число разів, то середня не зміниться;

Покажемо цю властивість середньої арифметичної на прикладі, припустимо що А=100

Денний виробіток ткачих, м (x)	Кількість ткачих (f)	Розрахунок середньої при зменшенні частоти на число А	Розрахунок середньої при збільшенні частоти на число А
f/100	(xf)	f*100	(xf)

		0,7 1,7 0,6	32,2 34,8
Всього		-		-

4. Алгебраїчна сума відхилень усіх варіант від середньої дорівнює нулю;

Денний виробіток ткачих, м (x)	Кількість ткачих (f)	Відхилення усіх варіант від середньої

		52-46=+6 52-50=+2 52-54=-2 52-58=-6
Всього

Тема: 5 Аналіз рядів розподілу

1. Мода та порядок її обчислення

2. Медіана та порядок її обчислення

1. Мода та порядок її обчислення

Середня арифметична і середня гармонійна дають узагальнену характеристику міри тієї або іншої ознаки про досліджувану сукупність. Вони виражаються здебільш розмірами, що не збігаються з конкретними значеннями ознаки. У деяких випадках виникає необхідність дати таку характеристику типових розмірів ознаки, що є конкретним числом, наявним у варіаційному ряду.

Наприклад , при встановленні розміру взуття або одягу, що має найбільший попит споживача, обчислена середня арифметична величина не дає конкретного розміру, тому що в результаті обчислення можна одержати середній розмір взуття або одягу, що не відповідає існуючим конкретним розмірам (число 40,4 не відповідає існуючим розмірам взуття, так як в дійсності є розміри 40 і 41).

Тому в статистиці застосовуються такі види середніх величин, як мода і медіана.

Мода - значення ознаки (варіанти) котра частіше за все зустрічається в досліджуваній сукупності (тобто варіанта яка має найбільшу частоту).

Способи розрахунку моди залежать від характеру вихідних даних. Так, в дискретному ряді розподілу модою є варіанта, яка має найбільшу частоту.

Наприклад: припустимо , що 9 робітників бригади мають наступні тарифні розряди: 4 3 4 5 3 3 6 2 6 . Так у даній бригаді більше усього робітників 3- го розряду, цей тарифний розряд і буде модальним.

В інтервальному ряді розподілу моду визначають за формулою:

де:

- мода

- мінімальне значення ознаки в модальному інтервалі

- величина модального інтервалу

- частота модального інтервалу

- частота інтервалу, що стоїть перед модальним інтервалом

- частота інтервалу, що стоїть після модального інтервалу

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Приклад	\|	Приклад

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.