
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Контрольні запитання i завдання
1. Яке спостереження називають вибірковим?
2. У чому полягають переваги вибіркового спостереження?
3. У якій послідовності проводиться вибіркове спостереження?
4. Назвіть види i способи відбору у вибіркову сукупність.
5. Як здійснюють випадковий i механічний відбір?
6. У чому полягає особливіть типового (районованого) та серійного відбору?
7. Що таке моментне спостереження?
8. Чому при вибірковому спостереженні виникають помилки, як їx класифікують?
9. Чим відрізняється випадкова помилка репрезентативнocтi від систематичної? Чи можна її уникнути?
10.Як визначається помилка вибірки?
11.Чим відрізняєтъся гранична помилка вибірки від середньої (стандартної)?
12.Як визначають помилки вибірки для середньої i частки?
13.Чи впливає обсяг вибірки на її точность i якою мipoю?
14.Від чого залежить обсяг вибірки?
15.Як визначають необхідну чисельність вибірки для середньої i частки в разі повторного i безповторного відбору?
16.Як поширюються дані вибіркового спостереження на генеральну сукупність?
17.При вибірковому обстеженні 3% виробів партії готової продукції (випадковий безповторний відбір) одержані такі дані про вміст вологи у виробах:
| Відсоток вологи | Кількість виробів |
| До 15 | |
| 15-17 | |
| 17-19 | |
| 19-21 | |
| 21-23 |
Визначити з ймовірністю 0,997 граничну помилку вибірки для середньої вологості всієї партії готової продукції.
18. 5%-не обстеження робітниць фабрики за виробітком продукції (механічний відбір) характеризується такими даними:
| Виробіток тканин, пог. м. | 50-52 | 52-54 | 54-56 | 56-58 | 58-60 |
| Кількість робітниць |
Визначити з ймовірністю 0;954 граничну помилку вибірки та довірчі інтервали для генеральної середньої та генеральної частки.
19. За даними 20%-ного вибіркового обстеження домогосподарств витрати населения області на побутові послуги становили:
| Тип поселения | Число обстежених домогосподарств | Витрати на одного члена, грн. на місяць | Дисперсія витрат |
| Місто Село |
Для кожного типу поселення визначити відносні помилки вибірки з ймовірністю 0,954 i порівняти їx.
20. Із сукупності 2000 робітників методом випадкового безповторного відбору відібрано 200 робітнків, у яких середній виробничий стаж виявився 8 років, а дисперсія стажу роботи — 30. Визначити можливі межі середнього виробничого стажу роботи для вcix робітників підприємства.
21. 3 метою визначення частки браку виготовлених деталей було проведено 10%-ну типову вибірку з відбором одиниць пропорційно чисельності одиниць у типових групах.
| Тип верстатів | Виробіток одного верстата. шт. | Процент браку за даними вибірки |
| 1,8 | ||
| 2,5 | ||
| 3,0 | ||
| 1,5 | ||
| 1,0 |
З ймовірністю 0,997 визначити межі, в яких лежить частка браку в усій партії деталей, виготовлених на вcix верстатах.
22. Проведено вибіркове обстеження втрат зерна озимої пшениці через несвоєчасне збирання врожаю. Кількістъ пробних ділянок визначалася пропорційно посіву відповідного сорту пшениці (типова вибірка). Результати обстеження такі:
| Сорт пшениці | Кількість пробних ділянок | Втрати зерна, ц/га | Дисперсія втрат зерна |
| А В С | 6,4 7,8 10,3 |
Визначити:
• середі втрати зерна у розрахунку на одну пробну ділянку та довірчі межі середніх втрат з ймовірністю 0,954;
• мінімально достатній обсяг вибірки, при якому похибка вибірки з тією самою ймовірністю не перевищить і ц/га.
23.Вперше організовується моментне спостереження за ефективністю використання 50 одиниць виробничого устаткування. Скільки спостережень необхідно провести, щоб похибка вибірки для частки устаткування, що не працює, з ймовірністю 0,954 не перевищувала 2%. За умови, що спостереження триватиме 10 днів, скільки спостережень щоденно необхідно за кожною одиницею устаткування?
24.На лісовому масиві в 400га передбачається визначити загальний запас деревини. Пробні площі становлять 0,1га. За даними попередніх обстежень дисперсія виходу деревини з 0,іга становила 6. Скільки пробних площ необхщно обстежити, щоб похибка вибірки з ймовірністю 0,954 не перевищувала 0,5м3.
25.Визначити необхідну чисельність вибірки iз 12 тис. робітників для вибіркового обстеження з ймовірністю 0,997 i граничною помилкою вибірки 0,5 чол., якщо за попередніми дослідженнями дисперсія становила 10.
Статистичний словник
Абсолютні статистичні величини характеризують розміри соціально-економічних явищ — обсяги сукупності або обсяги значень певних ознак.
Абсолютний приріст (зменшення) - — це різниця рівнів динамічного ряду
— це різниця рівнів динамічного ряду
ланцюгові  , базисні
, базисні  .
.
Абсолютне значення 1%приросту показує, чого вартий один процент; розраховується як співвідношення абсолютного приросту і темпу приросту. Алгебраїчно це співвідношення дорівнює 0,01 рівня, взятого за базу порівняння:

|
Абсолютна зміна в індексній моделі визначається як різниця між чисельником та знаменником відповідного індексу.
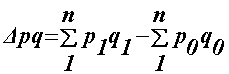
|
Б
Базисні характеристики динаміки - показники, в яких база порівняння постійна.
Багатовимірна середня -середня величина з відносних m ознак, яка є інтегральною оцінкоюj- го елемента сукупності

|
В
Варіаційний розмах характеризує діапазон варіації, це різниця між максимальним і мінімальним значеннями
| ознаки: | 
|
Варіювальні ознаки - ознаки, значення яких коливається серед окремих одиниць сукупності
Відносні величини- характеризують кількісні співвідношення різнойменних чи однойменних показників
Відносні величини інтенсивності - характеризують ступінь поширення явища у певному середовищі
Відносні величини динаміки - характеризують напрямок та інтенсивність зміни явища у часі, розраховуються співвідношенням значень показника за два періоди чи моменти часу
Відносні величини територіально-просторого порівняння- є результатом співвідношення однойменних показників, що характеризують різні об'єкти (підприємства, галузі) або території (міста, регіони, країни) і мають однакову часову визначеність.
Відносні величини структури - характеризують склад, структуру сукупності за тією чи іншою ознакою, обчислюється відношенням розміру складової частини до загального підсумку. Відносні величини структури називають частками, сума їх становить 1 або 100%.
Відносними величинами координації - єспіввідношення між окремими складовими сукупності
Внутрішньогрупова дисперсія розраховується для кожної j-ї групи:
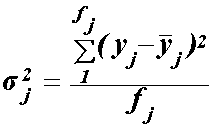
|
деyj — значення ознаки окремих елементів сукупності.
де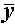 j — значення ознаки середнє по j-ій групі .
j — значення ознаки середнє по j-ій групі .
Д
Динамічний ряд -це розміщені у хронологічній послідовності значення певного статистичного показника.
| Дисперсія - середній квадрат відхилень окремих значень xj від його середнього значення |
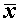
|
Для ознак метричної шкали розрахунок дисперсії ведеться за формулами для згрупованих даних.

|
| Дисперсія частки розраховується як добуток часток | 
|
З
Загальна дисперсіяхарактеризує варіацію результативної ознаки у за рахунок впливу всіх причин.
| Зведениміндексом вартості товарівє відносна зміна агрегату | 
| в цілому |
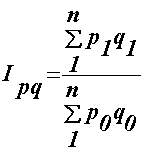
|
І
| Індекс— це відносна величина, яка характеризує зміну явища у часі, просторі або ступінь відхилення від стандарту. |
| Iндивідуальний індекс цін |

|
| Індекси | 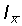
| характеризує відносну зміну середньої величини в цілому за рахунок обох факторів: |
| ознаки | хj | та структури сукупності | dj. |
| Індекс змінного складу |
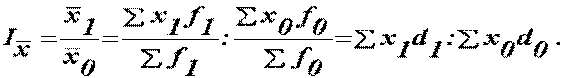
|
| Індекс фіксованого складу Ix показує зміну середньої величини за рахунок зміни тільки значень ознаки за незмінної структури сукупності: |
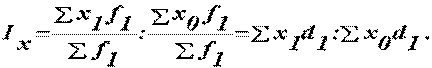
|
| Індекс структурних зрушень Id показує зміну середньої за рахунок зрушень у складі сукупності: |
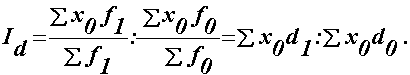
|
| Інтервальні показникі характеризують явище за певний час (день, місяць, рік), наприклад, експорт товарів та послуг за рік, приватизація нерухомості за квартал. |
К
| Квадратичний коефіцієнт варіації - | 
|
| Коефіцієнт осциляції - | 
| відношення міжгрупової дисперсії до загальної,оцінює ступінь щільності |
| звязку між ознаками. |
Кореляційне відношення 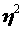 - цевідношення міжгрупової дисперсії до загальної, - цевідношення міжгрупової дисперсії до загальної,
|
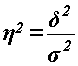
|
Л
| Ланцюгові характеристики динаміки - показники, в яких база порівняння постійна. |
| Лінійний коефіцієнт варіації | 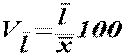
|
М
МодаМ0–це найпоширеніше значення ознаки, тобто варіанта, яка в ряду розподілу має найбільшу частоту (частку). В інтервальному ряду обчислюється за формулою:

Медіана Ме– це варіанта, яка припадає на середину упорядкованого ряду розподілу і ділить його на дві рівні за обсягом частини. В інтервальному ряду обчислюється за формулою:

|
де x0 та h — відповідно нижня межа та ширина медіанного інтервалу;
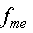
| — частота медіанного інтервалу; | 
| – кумулятивна частота передмедіанного інтервалу. |
Моментні показники -показники, які характеризують явище на певний момент часу: чисельність населення на початок року, залишки обігових коштів на початок місяця.
| Міжгрупова дисперсія обчислюється за формулою |
 , ,
|
| де | 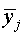
| та | 
| – відповідно середня j - ї групи та загальна середня варіюючої ознаки y; |
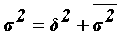
|
Р
Ряд розподілу - ряд цифр, що характеризують розподіл елементів сукупності за значенням варіювальної ознаки прискорення (+) чи уповільнення (–) динаміки.
С
| Середня величина — це узагальнююча міра варіювальної ознаки, що характеризує її рівень у розрахунку на одиницю сукупності. За даними ряду розподілу середня розраховується як арифметична зважена: |
| на основі частот | на основі часток |

|
| де | m — число груп, | fj | - частота j-групи, | dj | - частота j-групи. |
| Середня арифметична —використовується для осереднення прямих значень ознак шляхом їх підсумовування. ЇЇ логічна формула має вигляд |
| Середня арифметична проставикористовується якщо дані незгруповані де х — окремі значення ознаки, п — обсяг сукупності. |
| Середня з групових дисперсій- |
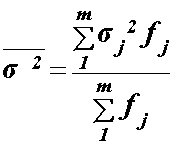
|
| Середня хронологічна - |
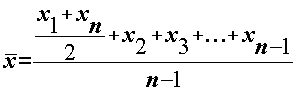
|
| ,де п — число моментів. |
| Середній темп зростаннярозраховується за формулою середньої геометричної: |
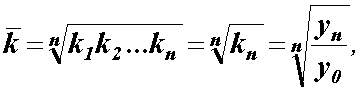
|
де п — число ланцюгових темпів зростання.
| Середній абсолютний приріст розраховується як середня арифметична проста з ланцюгових абсолютних приростів: |

|
| де n — число ланцюгових абсолютних приростів. |
| Статистичне зведення-класифікація та агрегування первинних статистичних даних. |
Середнє лінійнє відхилення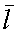 -модуль відхилень індивідуальних значень ознаки від середнього його значення. -модуль відхилень індивідуальних значень ознаки від середнього його значення.
|
| Для незгрупованих даних розраховується за формулою: |
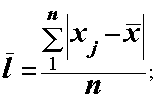
|
| Для згрупованих даних - |
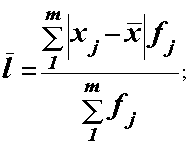
|
| Середнє квадратичнє відхилення -корінь квадратний з дисперсії. |
| Для незгрупованих даних визначається за формулою: |
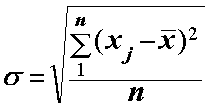
|
| Для згрупованих даних: |
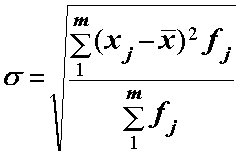
|
| Статистичне групування - розподіл статистичної сукупності на групи та підгрупи за однією або декількома ознаками. |
| Статистична таблиця- див. тему 2. |
| Статистичний показник — це узагальнююча характеристика соціально-економічного явища чи процесу, в якій поєднуються якісна та кількісна визначеність останнього. |
| Середня гармонічна використовується для осереднення обернених індивідуальних значень ознак шляхом їх підсумовування |
Середня геометрична визначається як добуток відносних величин динаміки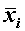 , які є кратним співвідношеннямі-го значення показника до попереднього (і–1). Формула середньої геометричної простої , які є кратним співвідношеннямі-го значення показника до попереднього (і–1). Формула середньої геометричної простої
|

|
деП — символ добутку; п — число осереднюваних величин.
| Середньозважена арифметична - |
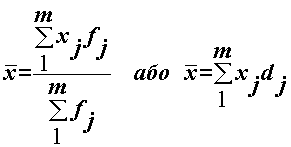
| |||||
| де | 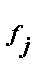
| –частота; | 
| – частка | j-ї групи. |
| Cередня гармонічна зважена - |

|
де zj – обсяг значень ознаки, тобто 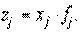
|
| Середньозважений індекс — це середній з індивідуальних індексів, зважених на обсяги, що мають однакову розмірність та зафіксовані на незмінному рівні. Середньозважений індекс цін визначають за формулою середньої зваженої |
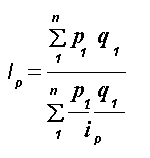
|
| Середньозважений індекс фізичного обсягу визначають за формулою середньої арифметичної зваженої |

|
Т
Темп зростання kt розраховується як відношення рівнів ряду; виражається коефіцієнтом або процентом:
Темп приросту  показує, на скільки процентів рівень показує, на скільки процентів рівень  більше (менше) рівня, взятого за базу порівняння. Його можна визначити як відношення абсолютного приросту до бази порівняння або безпосередньо на основі темпу зростання. більше (менше) рівня, взятого за базу порівняння. Його можна визначити як відношення абсолютного приросту до бази порівняння або безпосередньо на основі темпу зростання.
|
Читайте також:
- V. Завдання.
- VІ. Підсумки уроку і повідомлення домашнього завдання.
- Адаптація персоналу: цілі та завдання. Введення у посаду
- Адвокатура в Україні: основні завдання і функції
- АКТУАЛЬНI ПРОБЛЕМИ І ЗАВДАННЯ КУРСУ РОЗМIЩЕННЯ ПРОДУКТИВНИХ СИЛ УКРАЇНИ
- Актуальність і завдання курсу безпека життєдіяльності. 1.1. Проблема безпеки людини в сучасних умовах.
- Аналіз руху грошових коштів у контексті нової фінансової звітності Важливим завданням аналізу фінансового стану підприємства є оцінка руху грошових коштів підприємства.
- Аудит, його мета та завдання
- Багатокритеріальні завдання оптимального керування
- Багатокритерійні завдання і можливі шляхи їхнього рішення.
- Безпека життєдіяльності людини – найважливіше завдання людської цивілізації
- Бесіда за запитаннями.
| <== попередня сторінка | | | наступна сторінка ==> |
| Генеральної і вибіркової сукупностей | | | Об'єкти управлінського обліку |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |