• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

ЛЕКЦІЯ ХХII

ТЕМА: ЕЛЕМЕНТИ КВАНТОВОЇ МЕХАНІКИ

ПЛАН

1. Корпускулярно-хвильовий дуалізм. Гіпотеза Луї де Бройля.

2. Співвідношення невизначеності Гейзенберга.

3. Хвильова функція та її статистичний зміст.

4. Рівняння Шредінгера.

5. Рівняння Шредінгера для атома водню. Квантові числа.

6. Спін електрона. Дослід Штерна і Герлаха.

7. Принцип Паулі.

8. Розподіл електронів у атомі за станами.

1. Розглянена нами теорія Бора була значним кроком у розвитку теорії атомів.

Вона показала:

1) неспроможність застосування законів класичної фізики до явищ у середині атомів;

2) визначне значення квантових законів у мікросвіті.

Однак вона

1) не змогла побудувати теорію атома гелію,

2) їй була притаманна внутрішня суперечність.

У зв’язку з цим виникло питання про те, наскільки повним є уявлення про електрона як механічної частки з певними координатами та імпульсами.

Якісним кроком на шляху до нових уявлень була гіпотеза Луї де Бройля про те, що корпускулярно-хвильовий дуалізм властивий не тільки електромагнітним хвилям, але й будь-яким елементарним частинкам.

Таким чином, потоку елементарних частинок, які поширюються зі швидкістю v, відповідає певна електромагнітна хвиля з довжиною хвилі l (тобто поток частинок володіє властивостями плоскої хвилі).

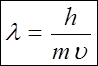(1) 1924 р.

l - довжина хвилі,

h - стала Планка.

Якщо u® c;

(1а)

Експериментальне підтвердження цього - досліди Девідсона і Джермера із розсіяння електронів на монокристалі Нікеля, при цьому спостерігалось явище дифракції електронів (чисто хвильовий ефект).

І

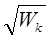
Наявність max і min не можна було пояснити з законами класичної фізики. Однак найбільш дивне було в тому, що l електрона підрахована з цього досліду збігалася з такою, що була підрахована за формулою Вульфа-Брега, що дійсно пояснювала наявність у електроні хвильових властивостей.

2. Класична механіка стан будь-якої матеріальної точки визначає певними значеннями координат та часу.

r = r (x, y, z, t)

А як же бути з описом стану частинки у мікросвіті за умови наявності у ній хвильових властивостей згідно з гіпотезою де Бройля?

Припустимо, що частинка знаходиться у деякій кінцевій області простору розмірами Dx, Dy, Dz. Можна припустити, що ця частинка у такому об’ємі буде приймати такі значення імпульсу Dp_x, Dp_y, Dp_z, які задовольняють співвідношенням Гейзенберга.

Dp_x ^. Dx ³ h

Dp_y ^. Dy ³ h

Dр_z ^. Dz ³ h

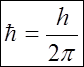(2)

Формула показує, що чим з більшою точністю Dx відома координата х, тим більша невизначеність у імпульсі Dp_x ® ¥. Якщо частинка знаходиться у збудженому стані деякий час Dt, володіючи енергією Е, то її енергія також може бути задана тільки з точністю DЕ.

- співвідношення невизначеностей для енергій є одним із фундаментальних принципів квантової механіки (якщо електрон падає на ядро v Þ 0, то p = 0. Це суперечить основним положенням квантової механіки).

3. Із розглянутих вище двох питань видно, що описувати по-старому стан частинки не можна.

А як же бути?!

Для опису повединки мікрооб’єктів уводять поняття хвильової функції Y (x, y, z, t). Таким чином,

(3)

dW - імовірність того, що частинка знаходиться в елементі простору

dV = dx dy dz.

Але фізичний зміст має не сама функція, а квадрат її модуля |Y|².

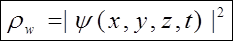(4)

r_w - густина імовірності, як раз вона і визначає ймовірність перебування частинки у даній точці простору.

Слід сказати, що функція задовольняє такій вимозі нормування:

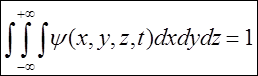(5) - умова нормування функції.

Фізичний зміст (5) у тому, що перебування частинки де-не-де у просторі є достовірною подією, ймовірність якої дорівнює 1.

4. Найважливіша проблема квантової механіки - знаходження рівняння аналогічного рівняння Ньютона у класичній механіці. Таке рівняння виведено Шредінгером у 1936 р. Це було рівняння для Y - функції:

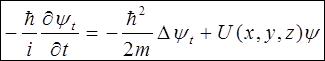(6)

m - маса частинки, яка має потенціальну енергію U(x, y, z)

i - уявна одиниця,

D - оператор Лапласа.

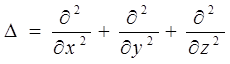
Для більшості фізичних явищ особливо важливим є знаходження незалежних від часу рішень рівняння Шредінгера, які називаються стаціонарними.

Для цього випадку

(7)

Підставивши (7) у (6),

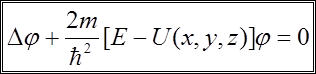(8)

- рівняння Шредінгера для стаціонарних станів.

Е - повна енергія частинки, яка рухається у потенціальному полі з енергією U.

Математика дає розв’язок рівняння (8): це дає набір j_i - власних функцій, які задовольняють рішення (8) та набір Е_і - власних значень енергії.

Таким чином, опис руху частинки зводиться до рішення рівняння Шредінгера, тобто до знаходження j_i та Е_і.

5. Застосуємо рівняння (8) до опису поведінки електрона в атомі водню. Можна показати на основі теорії діференційних рівнянь, що рівняння типу (8) мають рішення, які задовольняють вимоги однозначності, кінцевості та безперервності хвильової функції і її першої похідної тільки при таких значеннях власних енергії:

(9)

n = 1, 2, 3...

Із формули (9) видно, що ми маємо дискретний спектр власних значень енергії, котрі отримали на основі рішення рівняння Шредінгера без якихось додаткових застосувань різних положень, як це було у теорії Бора. Ця формула в точності збігається з аналогічним результатом теорії Бора (8) по передньої лекції.

Із (9) випливає фізично, що всі значення E_n < 0, а з цього виходить, що стан електрона є “зв’язаним”, тобто математично його стан можна описати як його знаходження у гіперболічній потенціальній ямі.

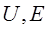
r

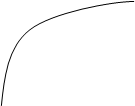
Найнижчий рівень (n=1) відповідає основному станові системи, а всі рівні E_n>E₁ (n=2,3...) - збуджені стани. Зі збільшенням n рівні будуть ще тісніше, а при n®¥, Е®0. Слід відмітити, що випадок з E_n>0 теж може випливати із розв’язання рівняння Шредінгера. Фізично це означає рух електрона поблизу ядра або на ¥, а це і є іонізація.

n = 1; z = 1;

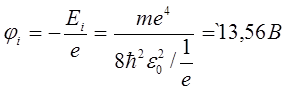
У квантовій механіці доводиться, що рівняння Шредінгера задовольняють тільки такі власні функції, що визначаються певними квантовими числами. Введемо числа:

1) n - головне квантове число, згідно з (9) воно приймає значення:

1)

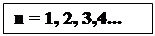
(10)

Фізичний зміст n полягає у тому, що воно визначає номер енергетичного рівня електрона в атомі і приймає тільки дискретні значення.

2) Із рішення рівняння Шредінгера випливає, що момент імпульсу електрона (механічний орбітальний момент) теж квантується за формулою

(11)

l - орбітальне квантове число, яке при заданому n приймає такі значення:

l = 0, 1, 2, 3... (n-1) (12)

Фізичний зміст l полягає в тому, що воно визначає момент імпульсу електрона в атомі і кожному значенню n відповідає орбітальне квантове число.

Згідно з теорією Бора припускається, що при прикладенні до атома зовнішнього магнітного поля вектори механічного моменту L і магнітного моменту `P_n будуть орієнтовані довільним чином відносно напрямку зовнішнього магнітного поля.

Ця помилка усувається у квантовій механіці введенням просторового квантування.

Із розв’язання рівняння Шредінгера виходить:`L_e може приймати не всі орієнтації у просторі, а тільки такі, при яких квантується його проекція на напрямок зовнішнього магнітного поля:

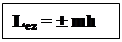
(13)

де Lez – проекція механічного моменту на напрямок зовнішнього магнітного поля.

3) m – магнітне квантове число

(14)

Видно із (11), (13), (14), що L_e може приймати (2l + 1) значень.

6. Для підтвердження ідеї просторового квантування Штерном і Герлахом у 1926 р. були проведені досліди з вимірювання магнітних моментів атомів різних хімічних елементів за величиною сили, діючої на атом у неоднорідному магнітному полі.

+ A

10^-5 мм рт. ст.

S N

- Ag

Атоми срібла, за даними дослідами, відхилялися двояким чином у магнітному полі, що вказувало і відповідало двом орієнтаціям магнітного моменту атома. Але стан електронів у атомах розглядуваних хімічних елементів відповідали значенням l = 0 та m=0 ?

Квантування якого моменту було знайдено ?

Для того, щоб результати досліду відповідали основним положенням квантової механіки, треба було ввести крім орбітального моменту електрона ` L<sub>e</sub>, власний механічний момент електрона `L_es (спін) та власний магнітний момент електрона `P_es.

Спін електрона ніяким чином не пов’язаний із рухом електрона у просторі.

Спін– фундаментальна властивість будь-якої частинки. Згідно з основними положеннями квантової механіки визначається:

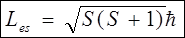(15)

S– спінове квантове число.

Аналогічно раніше введеному може бути 2s+1=2; S=1/2.

Для спіну також характерне вторинне квантування

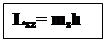
(16)

m_s– магнітне спінове квантове число.

4) m_s=±1/2

7. Таким чином, для характеристики електронного стану електрона в атомі треба задати тільки значення квантових чисел:

n, l, m, m_s

`r =`r ( x, y, z, t) Þ z= z( n, l, m, m_s )

Зв’язок між цими числами регулюється принципом Паулі (1927 р.):

Читайте також:

1. Вид заняття: лекція
2. Вид заняття: лекція
3. Вид заняття: лекція
4. Вид заняття: лекція
5. Вид заняття: лекція
6. Вступна лекція
7. Вступна лекція 1. Методологічні аспекти технічного регулювання у
8. Клітинна селекція рослин.
9. Колекція фонограм з голосами осіб, які анонімно повідомляли про загрозу вибуху
10. ЛЕКЦІЯ (4): Мануфактурний період світової економіки
11. Лекція - Геополітика держави на міжнародній арені
12. Лекція 02.04.2013

Переглядів: 905