• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Означення випадкових подій та обчислення їх ймовірностей

Випадкові події

Випробуванням називається експеримент, який можна проводити в однакових умовах (принаймні теоретично) будь-яке число разів. Найпростіший результат випробування називається елементарною подією або наслідком і позначається w. При випробуванні обов'язково настає лише один наслідок. Множина всіх можливих наслідків випробуван­ня називається основним простором або простором елемен­тарних подій і позначається W. Випадковою подією (подією) називається будь-яка підмножина A простору W, тобто будь-яка множина наслідків. Наслідки, які утворюють подію A, називають сприятливими для A (w Î A) Подія A настає тоді й тільки тоді, коли настає елементарна подія (наслідок), сприятлива для A. Порожня множина Ø і сама множина W, розглядувані як підмножини основного про­стору, називаються відповідно неможливою і вірогідною по­діями.

Оскільки подія означається як множина елементар­них подій, то над подіями можна виконувати такі ж операції, як і над множинами.

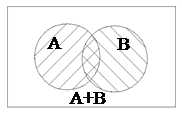Сумою подій А і В називається така подія С, яка настає тоді, коли настає принаймні одна з подій А або В, і позначається С = А + В або С = A 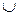В.

Добутком (суміщенням) подій А і В називається така подія С, яка настає тоді й тільки тоді, коли настають обидві події А і В, і познача­ється С = АВ або С = А ∩ В.

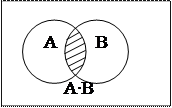
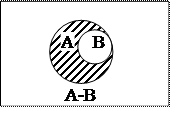Різницею подій А і В єподія С = А – В(С = А\В), яка полягає в тому, що Авідбувається, а В не відбувається.

Подія 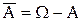(до­повнення множини А до W) називається протилежною до А. Ця подія полягає в тому, що А не відбувається. Очевидно, 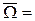Ø, .

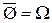Події А і В називаються несумісними, якщо поява од­нієї з них виключає появу іншої, тобто АВ =Ø.

Події А_і (і=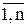) утворюють повну групу, якщо в ре­зультаті випробування обов'язково настане принаймні одна з них, тобто .

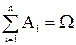Імовірністю Р (А) події А називається числова функція, яка визначена на множині подій і задовольняє такі три умо­ви (аксіоми ймовірності):

1) для довільної події А Ì W спра­ведлива нерівність Р (А) 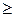0;

2) Р (W) = 1 (ймовірність вірогідної події дорівнює 1);

3) ймовірність суми попарно несумісних подій дорівнює сумі ймовірностей цих подій:

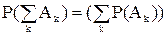(аксіоматичне означення ймовірності).

Будь-яке випробування, при якому простір елементарних подій W з скінченою множиною рівноможливих наслід­ків (тобто Р (w₁) = Р (w₂) =...= =Р (w_n) =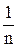), називається класичною схемою або схемою урн. У цьому випадку ймо­вірність будь-якої події А Ì W означається так:

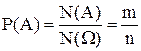, (7)

де N (А) =m — число елементів множини А (число на­слідків, які сприяють події А), N(W) =n — число елемен­тів множини W (число всіх наслідків випробування) (кла­сичне означення ймовірності).

Неважко перевірити, що так означена функція Р(А)має властивості: 0Р(А)1, Р (Ø) = 0, Р (W) = 1, Р (А+В) = Р(А) + Р(В), якщо АВ =Ø.

Нехай при n-разовому здійсненні досліду подія А відбулася k разів. Тоді відношення 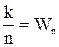називається частотою випадкової події, а границя 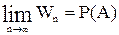— ймовірністю цієї події(статистичне означення ймовірності).

Читайте також:

1. Автододавання та автообчислення.
2. Алг W2 (ОБЧИСЛЕННЯ Y)
3. Алгебра випадкових подій
4. Алгебра подій
5. Аналітичні показники динаміки та прийоми їх обчислення
6. Багатовимірні випадкові величини. Система двох випадкових величин
7. База оподаткування, ставки податку та порядок обчислення.
8. Безвілля, його заподій і переборення.
9. Безпосереднє обчислення з використанням формули Ньютона-Лейбніца.
10. Види випадкових подій
11. Види середніх і способи їх обчислення
12. Визначення базисних подій. Ідентифікація ризику.

Переглядів: 875