• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Ступеневі середні

Залежно від мети дослідження обирається вид ступеневої середньої (арифметичної, геометричної тощо)

	Проста	Зважена
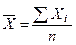
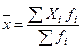
Середня арифметична якщо т = 1			У правовій статистиці широко застосовується для оцінки навантаження слідчих, прокурорів, суддів; обчислення середньої кількості осіб, що припадає на одну кримінальну справу, середнього віку засуджених, середнього строку розгляду справ тощо.
Середня геометрична якщо m = 0		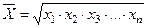	Використовується при розрахунку середньорічних темпів динаміки (приросту) юридично значущих явищ (х1, х2,..., хп – ланцюгові коефіцієнти динаміки)
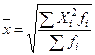
Середня квадратична якщо т = 2			Середня квадратична величина застосовується при вивченні зв’язків між досліджуваними явищами та їх причинами методом кореляційного аналізу та ін.
Середня гармонійна якщо т = -1			Дуже рідко застосовується у правовій. Це обернена величина середньої арифметичної й обчислюється, якщо є варіанти й добуток варіант на частоти, а частоти відсутні.

Середня арифметична являє собою відношення сумарної величини всіх варіант ознаки до їх чисельності.

Розглянемо розрахунок середньої арифметичної на прикладі:

річне навантаження 8 суддів міського суду, що спеціалізуються на розгляді цивільних справ, становило: 20, 40, 55, 70, 40, 20, 70, 40. Необхідно обчислити середнє річне навантаження на одного суддю. Застосовуємо

.

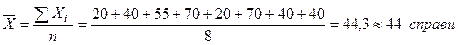Розрахунок проведений за середньою арифметичною простою. Вона застосовується, коли дані не згруповані або частоти однакові.

Якщо б ці дані були представлені у такому вигляді:

Таблиця 4

Кількість цивільних справ, х	Кількість суддів, f	то для розрахунку слід було скористатися формулою
		середньої зваженої:
Разом

При розрахунку середньої арифметичної часто не обов’язково знати вагу кожного індивідуального значення (варіант). В офіційній статистичній звітності є сумарні розміри. На основі цих узагальнених показників можна обчислити середню арифметичну величину.

В тому ж самому прикладі, знаючи кількість суддів (8) та їх загальне навантаження (20 + 40 + 55 + 70 + 40 + 20 + 70 + 40 = 315) можна розрахувати їх середнє навантаження:

315 : 7 = 45 справ

Ускладнюється розрахунок середньої арифметичної, якщо дані для розрахунку представлені у вигляді інтервального варіаційного ряду. Для цього інтервальний ряд потрібно перетворити у дискретний, тобто визначити середину інтервалу як напівсуму мінімального та максимального значення ознаки у кожній групі. І до формули як Х_і підставляється значення середини кожного інтервалу.

Читайте також:

1. А середній коефіцієнт росту в такому випадку визначається як
2. Абсолютні, відносні та середні величини.
3. Види злочинів за безпосереднім об'єктом
4. Види середніх величин
5. Види середніх величин та способи їх обрахування.
6. Види середніх величин та способи їх обрахування.
7. Види середніх і способи їх обчислення
8. Визначення середніх значень динамічних рядів
9. Визначення середнього абсолютного приросту середніх темпів зростання і приросту
10. Витрати виробництва та їх структура. Суть, види витрат. Закон спадної віддачі. Середні та граничні витрати.
11. Вищий середній нижчий
12. Вищий, середній, нижчий

Переглядів: 952