• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Частотний коефіцієнт передачі потужності

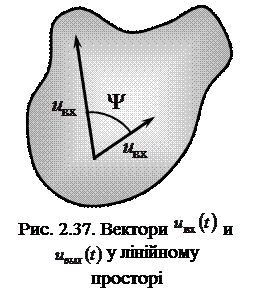Геометрична інтерпретація процесу перетворення сигналу в лінійній системі.Спектральний метод дозволяє наочно інтерпретувати перетворення сигналів, які відбуваються при їх проходженні через лінійні стаціонарні системи. З геометричних позицій, розглянутих у п. 2.1, системний оператор Т -це правило переходу від вектора деякого лінійного простору до нового вектора 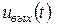(рис. 2.37). Як правило, функціональний простір сигналів можна вважати гільбертовим.

В самому загальному випадку можна стверджувати, що оператор змінює норму вектора 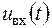, тобто Крім того, між векторами та виникає деякий кут

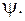
По формулі Релея (див. п. 1.4), енергія вихідного сигналу

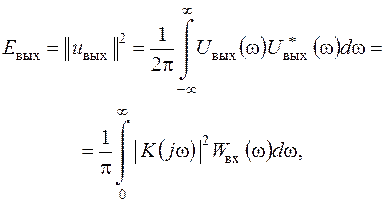
(2.65)

де 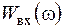– енергетичний спектр сигналу на вході.

Відповідно до формули (2.65), вихідний енергетичний спектр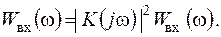

Величину

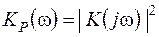
(2.66)

називають частотним коефіцієнтом передачі потужності системи на заданій частоті Оскільки цей коефіцієнт дійсний, обчислення енергії вихідного сигналу виявляється набагато більш простим завданням у порівнянні з пошуком самої форми вихідного сигналу.

4.1. Кут між векторами вхідного та вихідного сигналів

У п. 1.2 обговорювався спосіб порівняння двох сигналів, який базується на обчисленні кута 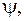утвореного векторами даних сигналів у гільбертовому просторі. Цю же ідею можна використовувати при порівнянні сигналів на вході та виході лінійної стаціонарної системи.

У багатьох випадках досить знати лише зміну енергії сигналу, який пройшов через лінійну систему.

Узагальнена формула Релея дозволяє виразити скалярний добуток цих сигналів через їхні спектральні щільності:

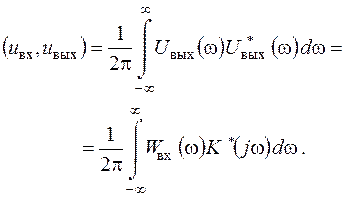
Оскільки уявна частина коефіцієнта передачі є непарною функцією частоти, остання формула спрощується:

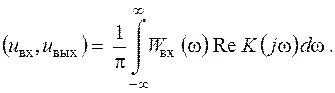
(2.68)

Кут між векторами вхідного та вихідного сигналів можна знайти зі співвідношення

(2.69)

Читайте також:

1. Ne і ne – поточне значення потужності і частоти обертання колінчастого вала.
2. А середній коефіцієнт росту в такому випадку визначається як
3. А. Фінансові коефіцієнти
4. А. Фінансові коефіцієнти
5. Активна та повна потужності
6. Активний опір ліній електропередачі
7. Аналіз коефіцієнтів цільової функції
8. Аналіз фінансових коефіцієнтів.
9. БАГАТОКАНАЛЬНІ СИСТЕМИ ПЕРЕДАЧІ ІНФОРМАЦІЇ
10. Безрозмірною характеристикою гідротрансформатора називається залежність коефіцієнтів пропорційності моментів насосного і турбінного коліс від його передаточного відношення.
11. Біноміальні коефіцієнти
12. Біохімічні чинники виникнення втоми при виконанні короткочасних вправ максимальної і субмаксимальної потужності

Переглядів: 1755