• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Приклад 1.

Знайти загальний розв’язок рівняння

Це лінійне рівняння виду (1), в якому 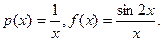Нехай y=UV, тоді y'=U'V+UV'. Маємо

Доберемо функцію так, щоб 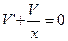, тоді

Інтегруючи перше з цих рівнянь, дістанемо

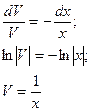
Підставивши значення у друге рівняння, дістанемо

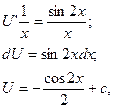
після чого знайдемо загальний розв’язок:

2. Рівняння, які зводяться до лінійних. Рівняння Бернуллі та Рікатті

Розглянемо класи рівнянь, які за допомогою певних перетворень можна звести до лінійних.

1.Рівнянням Бернуллі називається рівняння виду:

. (7)

Очевидно, при 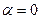це рівняння – лінійне, а при – з відокремлюваними змінними. Припускаючи , поділимо рівняння (7) на 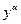, тоді матимемо рівняння виду:

.

Таким чином, заміною 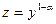рівняння Бернуллі зводиться до лінійного рівняння. Проте на практиці розв’язок рівняння Бернуллі зручніше шукати методом Бернуллі у вигляді 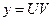, не зводячи його до лінійного рівняння. Слід зазначити, що при 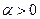, крім розв’язку 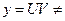, рівняння Бернуллі має розв’язок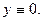

Читайте також:

1. Абсолютні синоніми (наприклад, власне мовні й запозичені) в одному тексті ділового стилю вживати не рекомендується.
2. Алгоритм однофакторного дисперсійного аналізу за Фішером. Приклад
3. Базові та прикладні класифікації
4. В чому полягає явище тунелювання через потенціальний бар’єр, наведіть приклади.
5. Визначення і приклади
6. Врахування витраті втрат електроенергії. Приклад складання електробалансу.
7. Головною метою наукової діяльності в системі вищої освіти повинен стати розвиток фундаментальних та приклад­них досліджень.
8. Деякі приклади застосування ППП
9. Дієслова з префіксом дис-виражають значення ліквідації дії, названої безпрефіксним дієсловом, наприклад: гармонізувати – дисгармонізувати, асоціювати – дисасоціювати.
10. Для одиничного і дрібносерійного виробництва норма витрати визначається як укрупнена, наприклад, на 1000 станко-годин роботи даного виду роботи устаткування
11. Додаток И - Приклад виконання ремонтного креслення деталі
12. Етикет – (прикріплювати) установлений порядок поведінки в товаристві, певному оточенні, наприклад, придворний етикет, дипломатичний етикет.

Переглядів: 737