
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Розмірний ефект у наносистемах
Загальні властивості наносистем
Класифікація нанокомпозитів.
2. Фізична хімія наносистем: Розмірність нанооб’єктів.Фрактальність.
3. Класична і квантово-механічна теорія наносистем.
4. Залежність фізико-хімічних властивостей від розмірів наооб’єктів. Вплив розмірів наночастинок на оптичні, магнітні, електрохімічні, механічні та каталітичні властивості.
Становлення міждисциплінарної галузі знань нанонауки відбулось на межі фізики, хімії і біології. В процесі еволюції уявлень про наносистеми оформились загальні принципи і підходи до їх аналізу незалежно від природи компонентів, що складають наносистему. Однак зрозуміти специфіку наносистем можна краще в межах однієї концептуальної позиції. Подальший виклад буде базуватись на висвітленні фізико-хімічних підходів при аналізі наносистем. Термін “нанохімія”, який виник в середині 90-х років минулого століття, означає, що при переході від атомно-молекулярного до надмолекулярного рівня структурної організації речовини з’являються особливі фізико-хімічні властивості речовини. Предметом нанохімії є фізико-хімічне дослідження наносистем.
Наносистему можна визначити як набір n-мірних нанооб’єктів – нуль-вимірних (0D) наночастинок (квантових точок), одновимірних (1D) волокон або нанодротин, двовимірних (2D) наноплівок, просторових (3D) нанокристалітів чи агрегатів, протяжність яких хоча б в одному вимірі лежить в межах від 0,1 до 100 нм, а також властивостей цих об’єктів і взаємодії між ними. Крім того, як обов’язковий компонент, до складу наносистеми також входитьнавколишнє середовище. Така система неоднорідна, бо, по-перше, неоднорідним є середовище, з іншого боку, нанотіла також неідентичні. Наносистеми належать до систем відкритого типу, тобто таких, які обмінюються з зовнішнім середовищем енергією та речовиною. З термодинамічного погляду наносистема нерівноважна і нестаціонарна, тому її властивості можна характеризувати функціями розподілу наночастинок за станами. Найголовнішою рисою наносистем є те, що будь-яка їхня властивість специфічно залежить від маси наночастинок. Залежність властивості від маси можна задати деякою функцією Хі(m), тоді як будь-яка властивість нанотіла характеризується власним значенням його маси mі і, відповідно до цієї маси, граничного розміру dmax.
Причина виникнення специфічних властивостей системи в наноінтервальному проміжку фізичних розмірів полягає у співрозмірності нанооб’єктів та дальнодії (протяжності дії) міжатомних сил. Коли розміри тіла менші від граничного (d < dmax), то всі атоми зближені настільки, що взаємодія кожного атома з будь-яким іншим суттєво впливає на властивість Хі. У протилежному випадку, коли розміри тіла перевищують граничний (d > dmax), то атоми віддалені один від одного настільки, що взаємодія між ними практично не впливає на властивість Хі. Через це можна вважати, що предметом нанохімії є вивчення об’єктів, в яких простежується значна взаємодія між атомами [1].
Стан наносистеми в будь-який проміжок часу визначається функціями розподілу нанотіл j(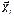 ,t) і середовища y(
,t) і середовища y(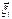 ,t) за параметрами стану частинок Хі і середовища xі. Дослідження системи зводиться до встановлення закономірностей зміни властивостей середовища і виявлення взаємозв’язку між функціями j(
,t) за параметрами стану частинок Хі і середовища xі. Дослідження системи зводиться до встановлення закономірностей зміни властивостей середовища і виявлення взаємозв’язку між функціями j(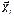 ,t) і y(
,t) і y(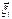 ,t) в процесі еволюції системи в часі. Стан кожної наночастинки в будь-який момент часу t визначається її масою m, просторовими координатами і швидкістю руху в лабораторній системі координат, відстанню до кожної з наночастинок системи, яка задається координатами {Yi}, а також параметрами стану кожного з атомів, які становлять частинку, тобто внутрішніми координатами наночастинки {Zi}. Зв’язок властивостей наносистеми з зовнішніми та внутрішніми параметрами загалом виражає співвідношення
,t) в процесі еволюції системи в часі. Стан кожної наночастинки в будь-який момент часу t визначається її масою m, просторовими координатами і швидкістю руху в лабораторній системі координат, відстанню до кожної з наночастинок системи, яка задається координатами {Yi}, а також параметрами стану кожного з атомів, які становлять частинку, тобто внутрішніми координатами наночастинки {Zi}. Зв’язок властивостей наносистеми з зовнішніми та внутрішніми параметрами загалом виражає співвідношення
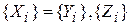 . .
| (1.1) |
У процесі еволюції наносистеми кожен із її складових атомів переходить з одного дозволеного стану в інший. Однак їхня кількість настільки значна, що зміну стану наночастинки можна характеризувати ймовірністю переходу Р із стану {Хi,0} в стан {Хi} протягом проміжку часу Dt
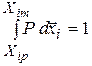 , ,
| (1.2) |
де Хiр і Хim – відповідно нижня і верхня межі дозволеного інтервалу зміни Хi. Інтегрування виразу (1.2) проводиться за всіма станами Хi.
Головне завдання теорії еволюції наносистем полягає в розрахунку функції ймовірності
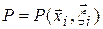 . .
| (1.3) |
Якщо відома функція ймовірності, то можна розрахувати функціонал Gі, який характеризує швидкість еволюції наносистеми
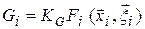 . .
| (1.4) |
Тут КG– кінетичний коефіцієнт; Fi(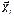 ,
,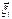 ) – рушійна сила елементарного процесу, відповідального за зміну внутрішніх Хi і зовнішніх параметрів
) – рушійна сила елементарного процесу, відповідального за зміну внутрішніх Хi і зовнішніх параметрів 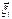 .
.
Наносистема – це сукупність нанотіл (нанооб’єктів) у багатовимірному фазовому просторі, координати точок якого збігаються з координатами нанотіл. Поверхню можна уявити у вигляді набору структурних елементів, до яких з ймовірністю Pj приєднуються атоми з середовища, а рушійною силою взаємодії є різниця вільних енергій середовища і центру на наночастинці або ступінь насичення розчину
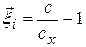 , ,
| (1.5) |
де c – концентрація атомів в середовищі; cx – розчинність наночастинки. Оскільки
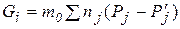 , ,
| (1.6) |
де m0 – маса атома; nj – кількість структурних елементів на поверхні наночастинки; P¢j – ймовірність відриву атома структурного елемента за одиницю часу, то для кінетичного коефіцієнта справджується співвідношення
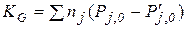 . .
| (1.7) |
Тут Pj,0 і P¢j,0 – частоти приєднання і відриву структурних елементів при 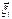 = 1.
= 1.
Теоретичний аналіз загальних кінетичних моделей наносистем утруднений через низку причин. Розрахунок стану наносистемами в певний момент часу охоплює розрахунок двох складових: внутрішньої Zi(m, 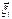 ) і зовнішньої y(
) і зовнішньої y(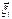 ,t). Детальний опис множини {Zi} передбачає необхідність введення параметрів внутрішньоатомного розподілу електронної густини, які можна отримати розв’язком відповідного рівняння Шрьодінгера. Однак, розв’язок подібного рівняння з задовільною точністю для ансамблю, який містить велику множину електронів і ядер, неможливий. Розрахунок функції зовнішньої складової y(
,t). Детальний опис множини {Zi} передбачає необхідність введення параметрів внутрішньоатомного розподілу електронної густини, які можна отримати розв’язком відповідного рівняння Шрьодінгера. Однак, розв’язок подібного рівняння з задовільною точністю для ансамблю, який містить велику множину електронів і ядер, неможливий. Розрахунок функції зовнішньої складової y(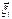 ,t), який можна провести методами статистичної термодинаміки, теж пов’язаний зі значними труднощами і вимагає введення низки спрощуючих припущень. Проблема особливо ускладнюється при спробі описати зміну стану наносистеми у часі.
,t), який можна провести методами статистичної термодинаміки, теж пов’язаний зі значними труднощами і вимагає введення низки спрощуючих припущень. Проблема особливо ускладнюється при спробі описати зміну стану наносистеми у часі.
На жаль, доводиться констатувати, що загальна теорія наносистем ще далека до завершення. Аналіз величезного масиву експериментальних даних проводять у рамках моделей, які описують поодинокі нанотіла у середовищі. Сюди належать моделі укрупнення, розчинення, переміщення у просторі, зміни форми, сорбційні, “заліковування” дефектів кристалічної ґратки, електричної та механічної поляризації тощо. При створенні загальних і часткових моделей наносистем було використано принцип розмірних ефектів двох типів: власного (або внутрішнього) і зовнішнього. Внутрішній розмірний ефект зумовлений поверхневими, об’ємними та хімічними властивостями частинок. Зовнішній розмірний ефект, по суті, є розмірнозалежним відкликом на дію зовнішніх сил, незалежних від внутрішнього ефекту [2]. Розміри наночастинок суттєво впливають на магнітні, електричні, оптичні властивості наносистем. Наприклад, залежність енергетичних властивостей сферичних наночастинок від їхнього розміру можна виразити співвідношенням
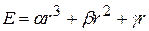 , ,
| (1.8) |
де r – радіус частинки; a, b, g – деякі константи. Перший член у співвідношенні (1.8) виражає об’ємну енергію, другий – поверхневу, третій характеризує поверхневий натяг.
1.5. Фрактальний аспект наносистем
Наносистеми – це типові відкриті нерівноважні, а отже, і нестабільні в часі, системи нанооб’єктів, які загалом “погано” організовані або стохастичні. Для їх опису мало придатні класичні підходи, які ґрунтуються на силогістиці Арістотеля, яка виходить з того, що все може бути локалізовано і має свої власні межі. Більш придатним видається альтернативний підхід Геракліта, який стверджував, що все перебуває у постійному русі і змінюється, а стабільність і гоместаз не є нормою. Логічним продовженням “лінії” Геракліта було відкриття теорії Хаосу, яка органічно об’єднала в собі інформатику, кібернетику, голографію, нелінійну динаміку і фрактальну геометрію.
1.5.1. Фрактали. Фрактальна геометрія
До недавнього часу природні об’єкти і їхню динаміку не вдавалося математично описати у закінченому вигляді. Причиною цього є те, що реальні об’єкти лише подібні до геометричних фігур: пагорби – це не конуси, ріки – не прямі і не регулярні криві, рівнини – не площини, каміння – не кулі і т. д. Результатом цього була недосконалість і нереальність перших спроб комп’ютерної графіки, неможливість моделювання складних поверхонь тощо. Формули, на підставі яких тепер розроблені алгоритми для моделювання форми хмар, структури рослин чи потоків товарів на ринках, були виведені зовсім недавно завдяки піонерським працям французького математика Бенуа Мандельброта, який ввів у вжиток поняття фракталу.
Термін “фрактал” походить від лат. fractus, що означає розколотий, роздрібнений, той, що складається з фрагментів. Загалом він означає структуру, складові частини якої подібні в певному сенсі до цілого [36]. В будь-якій фрактальній структурі довільно вибрана точка завжди є місцем розгалуження. Дроблення на частинки, які подібні до цілого, або перетворення, які повторюються, характеризуються зломами і самоподібністю. При цьому кожна точка злому характеризується відсутністю похідної.
Фрактали можуть бути лінійними і нелінійними. Лінійниминазивають фрактали, які можна описати лінійними функціями. Самоподібність тут реалізується у точній копії будь-якої частинки цілому. Значно багатші і різноманітніші нелінійні фрактали, які описуються нелінійними рівняннями. Самоподібність у нелінійних фракталів проявляється в деформованій копії частинки цілому. Ще одна особливість фракталів – їхній дробовий вимір. Розмірність одномірних геометричних об’єктів знаходиться в межах між нулем і одиницею, тоді як дво- та тривимірних – між 1 і 2 та між 2 і 3 відповідно. Дробовий вимір дозволяє розрахувати властивості, які не можуть бути чітко визначені іншим шляхом, як то ступінь нерівності, переривчастості (дискретності) або нестійкості об’єкта. Мандельброт виявив, що найпростіші нелінійні фрактали задаються квадратичними функціями, його можна реалізувати в комплексній площині шляхом ітераційної процедури (покрокове збільшення змінної на одиницю).
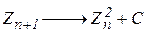 . .
| (1.96) |
Цей алгоритм дозволяє одержати числову послідовність, кожний наступний член якої рівний квадрату попереднього, зміненому на деяку величину С. Точки цієї послідовності будуть лежати не на прямій, а в площині. Вигляд фракталів залежно від значення постійної С наведено на рис. 1.36.
|
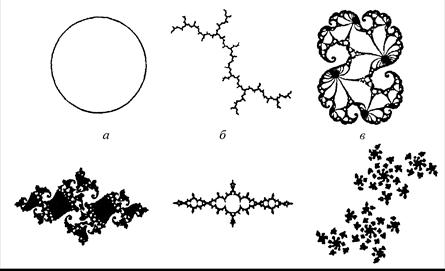
Рис. 1.36. Приклади нелінійних фракталів при різних значеннях параметра С (рівняння (1.96)): 0 (a); і (б); 0,27334+0,00742і (в); 0,74543+0,11301і (г); –0.125(д); 0,11301–0,67037і (е)

Рис. 1.37. Фрактал Мандельброта [37]
Якщо в ітераційній процедурі зафіксувати параметр Z, змінюючи С, то одержимо множину Мандельброта, графічне зображення якої загальновідоме як фрактал Мандельброта (рис. 1.37). Детально розглядаючи зображення, можна переконатись, що при його збільшенні проявляються все нові і нові форми, подібні, залежно від фантазії спостерігача, на морських коників чи згорнуті гілки тропічних рослин тощо. Проте ніколи один фрагмент системи не повторює інший, хоча є до нього подібний. Крім того, були виявлені так звані плаваючі молекули або пилинки, які нагадували маленькі острівці, що оточували основний об’єкт. Однак при детальнішому розгляді збільшеного зображення фрактала видно, що кожна така плаваюча молекула насправді підвішена на філігранній нитці, яка з’єднує її з іншими молекулами. При подальшому збільшенні виявляються нові молекули, кожна з яких за формою нагадує систему в цілому і одночасно чимось відрізняється від неї. Кожна молекула співвимірна з характерними виступами, які нагадують язики полум’я. В них неминуче виявляться нові молекули, що менші, але такі ж безконечно різнобічні: завжди подібні, але ніколи не ідентичні.
Вражаюча простота фрактальних алгоритмів і дивовижна величність форм нелінійних фракталів роблять фрактальну геометрію надзвичайно ефективним засобом для опису морфологічних властивостей природи. Якщо перефразувати на сучасний лад сформульоване на зорі природознавства Галілео Галілеєм твердження, що книга природи написана мовою кіл і трикутників, то можемо з впевненістю сказати, що ця книга написана мовою нелінійних фракталів. Дивовижні обриси берегових ліній і гірських хребтів, форми хмар, крони дерев, розгалуження кровоносних судин і нейронів, вспінені турбулентні потоки гірських річок – все це фрактали. Спільним в обрисах природніх об’єктів є своєрідна почерговість порядку і безпорядку-хаосу, гармонія яких є вищим принципом природи [38].
1.5.2. Фрактальна розмірність і методи її визначення
Теорію фракталів можна використати для аналізу як процесів, так і синтетичних (штучно створених) чи складних природних (ензими, протеїни, ДНК тощо) об’єктів: Недивлячись на невизначеність фрактальної розмірності процесу, фрактальний підхід успішно використовують для аналізу хімічних, електрохімічних і сорбційних процесів. Серед фрактальних наноструктур умовно можна виділити два типи об’єктів, а саме, регулярні і нерегулярні. Регулярні фрактали володіють симетрією самоподібності, тобто інваріантні до зміни форми у всіх напрямках. Ці об’єкти самовідображаються після зміни їхніх розмірів. В свою чергу нерегулярні фрактали неінваріантні відносно більшості операцій симетрії, наприклад, обертання чи відображення в просторі Евкліда, і не відображаються самі на себе при зміні довжини шкали. Їх ще називають статистично самоподібними фракталами, оскільки всі статистичні величини, які їх характеризують, інваріантні до зміни масштабу.
Статистично самоподібні фрактали придатні для моделювання лімітованих дифузією процесів кластер-кластерного агрегування, коли більші кластери утворюються в результаті об’єднання менших за розміром частинок [39]. Процес агрегування можна уявити як заповнення частинками центрів квадратної ґратки розмірами L´L, яке відбувається за законом випадку. Приймають, що сусідні зайняті центри належать одному і тому ж кластеру, а сам він може переміщатися в одному з чотирьох рівноймовірних напрямів у двовимірному просторі (у центри сусідніх квадратних комірок).
Загалом для статистично самоподібного фракталу критерій µ(l) в межах відстані l від точки на фрактальному об’єкті задається співвідношенням
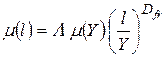 . .
| (1.97) |
Тут µ(Y) – критерій для зайнятої області розміром Y; Λ – стала, що залежить від типу описуваного процесу; Dfr – фрактальна розмірність. Параметр µ(l) може, зокрема, відповідати загальній масі М, а характеристична довжина l –загальному розмірові об’єкта L. В цьому випадку рівняння (1.97) набуде вигляду
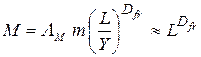 , ,
| (1.98) |
де ΛM – амплітуда або фактор форми, пов’язаний з лакунарністю (про що йтиметься далі), а m – маса складової частинки розміром Y. Ця масштабуюча залежність між масою і розмірами подібна до відповідної масштабуючої залежності (М » Ld) для евклідових об’єктів у евклідовому просторі, коли розмірність d може дорівнювати 1, 2 та 3. З рівняння (1.98) слідує, що фрактальна розмірність пов’язана з кількістю частинок N розміром Y на відстані L від точки на об’єкті визначається співвідношенням
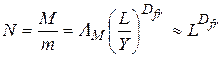 . .
| (1.99) |
Один з найпростіших методів визначення фрактальної розмірності ґрунтується на тому, що фрактал, будучи у d-вимірному просторі Евкліда, є покритий d-вимірною сіткою з розмірами комірок l. Тоді фрактальна розмірність еквівалента ємності сітки, яка визначається кількістю зайнятих частинками місць у сітці
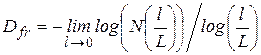 , ,
| (1.100) |
де N(l / L) – кількість заповнених елементів сітки. Однак стану, коли l→0, практично неможливо досягнути, тому оцінити Dfr можна, вимірявши залежність log (N(l / L))від log (l / L) в інтервалі l1 < l < l2, де l1 >Y (нижня межа), а l2 < L (верхня межа):
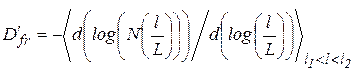 . .
| (1.101) |
Амплітуда (або фактор форми) ΛМ кількісно характеризує так звану лакунарність (від сл. лакуна – вільна порожнина): фрактали з більшою величиною амплітуди ΛМ заповнюють простір більш однорідно і тоді кажуть, що він менш лакунарний, тобто, у ньому є менше пустот. Як поняття лакунарності, так і фрактальної розмірності необхідно вживати для того, щоб знати як фрактальні об’єкти заповнюють простір, а також для повнішої характеристики геометрії об’єкта. Крім того, для багатьох реальних об’єктів є верхня межа характеристичної довжини ξ, яка може бути більшою порівняно з загальними розмірами об’єкта, але вище якої фрактальний масштаб більше не підтримується. Ця верхня межа є так званою кореляційною довжиною, вище якої структуру можна вважати однорідною і евклідовою. Фрактальність виникає для рівнів, нижчих від кореляційної довжини, і тоді рівняння (1.99) набуває вигляду
 , ,
| (1.102) |
де ΛМ – лакунарність, а параметр n враховує кількість (статистичних) копій фрактальної області, які містить об’єкт загальним розміром L . Для реальних об’єктів при визначенні фрактальної розмірності використовують сітки з квадратними чарунками розмірами l / ξ, а кількість комірок NT, потрібна для заповнення усієї сітки, становитиме
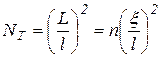 , ,
| (1.103) |
Ділення (1.102) на (1.103) дає вираз
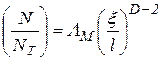 , ,
| (1.104) |
згідно з яким фрактальна розмірність (для l<ξ) виразиться співвідношенням
 . .
| (1.105) |
Кореляційну довжину можна оцінити, використовуючи автокореляційну функцію С(s), яка виражає ступінь кореляції у наборі послідовних експериментальних даних ¦(xn). Детальніше, означаючи d¦n як
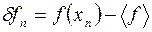
| (1.106) |
матимемо
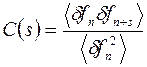 . .
| (1.107) |
Тут середні значення, наведене у дужках áñ, означають усереднення набору експериментальних даних {xn}, який еквівалентний множині місць у модельній сітці. В контексті модельних сіток, ¦(xn) відповідає ступеню заповнення у наборі xn. Ступінь заповнення дорівнює одиниці, якщо місце зайняте, і, навпаки, незайняті місця характеризуються нулем. Характеристичними величинамими цієї функції є значення С при s = 1 та значення s, коли С(s)=0. Перша величина характеризує ступінь кореляції, тоді як друга, відома як кореляційна довжина (ξ),характеризує протяжність лінійної кореляції. Якщо два фрактальні об’єкти ідентичні, то їх кореляційні довжини мають бути ідентичними.
1.5.3. Фрактальність наноструктурованих плівок кремнезему
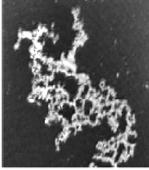
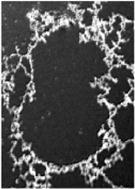
Еволюцію фрактальних структур та методику визначення їхньої фрактальної розмірності розглянемо на прикладі наноструктурованої плівки кремнезему, синтезованої гідролізом тетраметоксисилану. Мікрофотографії плівки SiO2, одержані на різних стадіях її росту, зображено на рис. 1.38. Ріст плівки починається лише після індукційного періоду, протягом якого забруднення на поверхні тефлонової підкладки, на якій формувалась плівка, діють як центри нуклеації. Центри нуклеації утворюють маленькі фібрили, які після досить короткого часу обрамляються світлими точками, що свідчить про нуклеацію вздовж волокон (рис. 1.38, а). Осадженню плівки передує утворення структур, зображених на рис. 1.38, б, однак їхня природа досі невідома і можна лише припустити, що вона пов’язана з орієнтацією частинок сурфактанта на поверхні підкладки. Наступний етап синтезу відповідає масовому утворенню дрібних частинок (рис. 1.38, в), які перебувають у броунівському русі і зіткнення яких між собою призводять до їхнього об’єднання у все більші частинки, аж до утворення фрактальних кластерів (рис. 1.38, г). При подальшому рості плівки фрактальний кластер спочатку стає більш відкритим (рис. 1.38, д), однак надалі фрактальна сітка суттєво ущільнюється (рис. 1.38, е) аж до остаточного утворення напівбезмежної плівки, структуру якої зображено на рис. 1.38, ж.
Для визначення фрактальної розмірності плівки було вибрано фрагменти її зображень, на яких світліші ділянки відповідали частинкам SiO2, тоді як темні – вільній поверхні рідкої фази (рис. 1.39, а–б). Однак реально маємо справу з зображенням на якому переважають відтінки сірого. Тож, для точнішого



а б в г


д е ж
Рис. 1.38. Мікрофотографії різних стадій росту плівки SiO2, зроблені під кутом Брюстера. На зображенні частинки кремнезему виглядають як світлі або сірі області, рідка поверхя має темний відтінок (опис мікрофотографій подано у тексті) [39].
розділення пікселів (мінімального елемента зображення), які відповідають зображенню частинок кремнезему і рідкої фази відповідно, необхідно врахувати насиченість сірого кольору. Для цього було введено спеціальну шкалу, яка показує кількість пікселів на зображенні залежно від ступеня насичення їхнього забарвлення. Як видно з рис. 1.39, в, одержана гістограма не має бімодального характеру, як цього слід було б сподіватися, виходячи з чорно-білого зображення. Тому на її основі неможливо вибрати пороговий рівень насиченості сірого забарвлення, вище якого піксель можна віднести до рідкої фази, тоді як всі світліші (менш насичені) – до структурованих наночастинок. Тому надалі як пороговий рівень використовували різницю у насиченості кольору пікселів (рівень затемненості), що відповідають твердій та рідкій фазі відповідно. Лише після цього реальні (фактично сірі) зображення переводили у чорно-білу комп’ютерну модель і далі аналізувалось за


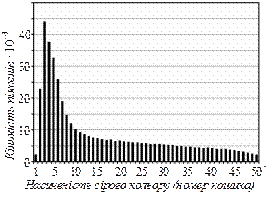
а б в
Рис. 1.39. Мікрофотографії двох різних кластерів кремнезему (а та б) та гістограма розподілу кількості пікселів згідно шкали насиченості сірого кольору (в)
Таблиця 1.8
Параметри фракталів кремнезему (рис. 1.39)
| Рівень затемненості | Частка твердої фракції* | Фрактальна розмірність Dfr | Лакуларність ln ΛM |
| Зображення (а) | |||
| 0,327 0,258 0,196 0,140 0,090 0,037 0,011 | 1,86±0,03 1,84±0,04 1,84±0,03 1,81±0,03 1,81±0,03 1,75±0,03 1,62±0,04 | 12,52 12,46 12,43 12,32 12,31 12,08 11,52 | |
| Зображення (б) | |||
| 0,213 0,159 0,114 0,078 0,048 0,021 0,007 | 1,57±0,03 1,57±0,03 1,57±0,03 1,46±0,04 1,29±0,03 1,18±,05 0,88±0,06 | 11,29 11,14 11,20 10,74 10,01 9,38 7,93 |
*Відношення кількості білих пікселів до їхньої загальної кількості на комп’ютерній моделі зображення
допомогою алгоритму, який полягав у підрахунку кількості заповнених чарунок і характеристичної відстані між фрактальними об’єктами. Використовуючи рівняння (1.101), було розраховано фрактальну розмірність і лакунарність. Параметри фракталів кремнезему, мікрофотографії яких зображені на (рис. 1.39, а–б), наведено у табл. 1.8 для різних рівнів затемненості. Коефіцієнт парної кореляції для всіх випадків був рівним 0,99. Отже структура кластерів кремнезену у плівці статистично ідентична, що відкриває можливості щодо комп’ютерного моделювання структур тонких плівок.
1.5.4. Аналіз кластер-кластерного агрегування електропровідних полімерів
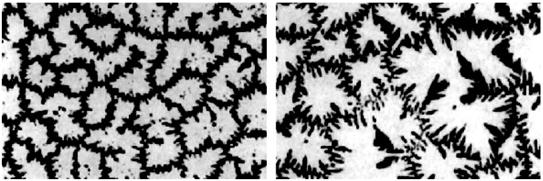
Процедура, подібна до вищеописаної, використовується також для визначення фрактальної розмірності електропровідних полімерів. Її особливістю є використання зображень, одержаних методом скануючої електронної мікроскопії. СЕМ-зображення після комп’ютерної обробки перетворюють у двокольорові і лише тоді аналізують щодо фрактальних характеристик полімерного шару, використовуючи як і у випадку кремнезему, модельну сітку. Зокрема фрактальна природа добре прослідковуються для тонких (3–4 мкм) плівок провідного політіофену з нанотрубчастою структурою (рис. 1.40, а–б) [40]. Результат комп’ютерної обробки цих зображень наведено на (рис. 1.40, в–г). Однак виявилося, що фрактальні характеристики морфології поверхневої плівки суттєво залежать від вибраного порогового значення k при перетворенні одержаного сірого 256-кольорового зображення. Це означає, що окремий (сірий) піксель на зображенні під час комп’ютерної обробки буде сприйматися як чорний (буде віднесений до субстрату) за умови, що його насиченість l буде більшою порівняно k, і навпаки, при k > l він вважатиметься білим (буде віднесений до полімеру). Залежність фрактальної розмірності від порогового значення k можна виразити наступною функцією
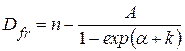 , ,
| (1.108) |

а б
в г
Рис. 1.40. СЕМ-зображення поверхневої мікроструктури тонких шарів нанотрубок провідного політіофену (збільшення у 9000 (а) та 20000 (б) разів), а також їхнє чорно-біле зображення після комп’ютерної обробки [40]
де n – так звана ідеальна фрактальна розмірність; a і А – підгоночні коефіцієнти. Тож, як випливає з наведеної формули, величина Dfr зростає зі збільшенням порогової величини сірого забарвлення для СЕМ-зображення.
Ще один підхід було реалізовано для аналізу фрактальності поліаналінових мікростержнів [41]. Він ґрунтується на припущенні, що процес електрохімічної полімеризації залежить від перенесення заряду вздовж макромолекулярного ланцюга, а тому електрична провідність лінійних макромолекулярних ланцюгів вища ніж для ланцюгів з розгалуженою структурою. Розгалуження зумовлюють стеричні перешкоди, які відповідають за зменшення перекривання p-орбіталей і, як результат, за підвищення опору протіканню електричного струму вздовж ланцюга.
Ймовірність приєднання мономерної ланки С6H4N до ростучого ланцюга пропорційна 1 / Ref, де Ref ефективний опір у розглянутій точці. На практиці визначальну роль для характеристики фрактальної структури відіграє відношення R / R0

де R0 та R – опір незбуреного ланцюга та опір при його поодинокому розгалуженні відповідно. Це дає змогу оцінити фрактальну природу провідного полімерного ланцюга, використовуючи електричні схеми-аналоги.
Зокрема, модель росту поліанілінового ланцюга з розгалуженнями і, відповідну йому, електричну схему зображено на рис. 1.41. Нехай ймовірність лінійного
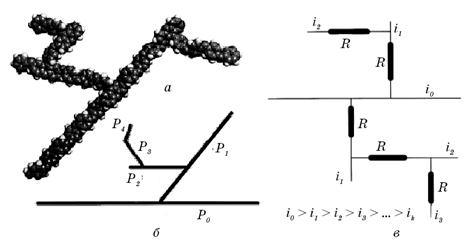
Рис. 1.41. Макромолекулярний ланцюг (а), мономерні ланки в структурі поліаніліну (б) і електрична схема фрактального росту поліаніліну (в)
приєднання мономерної ланки до зростаючого ланцюга становить Pi–1, тоді як ймовірність утворення нового розгалуження становитиме Рі. Тут індекс і означає порядок розгалуження. Тоді для розгалуження першого порядку можна записати
 , ,
| (1.109) |
або, в загальному випадку,
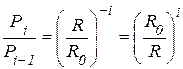 . .
| (1.110) |
Відношення R / R0, окрім ймовірності розгалуження, також характеризує швидкість реакції в новій гілці.
Фрактальна структура поліаніліну розраховувалась в широких межах зміни R / R0 – від 1 до 100. Було знайдено, що генеровані комп’ютером електричні моделі можуть бути віднесені за формою до мікростержнів при R / R0 = 5, 9, 16, 18 і 19, або до наноструктур при R / R0 = 2–5 та 18. При цьому величина фрактальної розмірності Dfr, розрахована на основі електричних моделей, збігається з даними тунельної електронної мікроскопії і становить 1,69 та 1,88 для мікростержів (R / R0 = 1 та 9) та для наноструктур (R / R0 = 5) відповідно.
1.5.5. Фрактальність поверхні
Переважна більшість природних і штучних процесів протікають за участю речовин, які перебувають у різних фазах, тобто в гетерогенних системах. Інтерпретація таких експериментальних даних здебільшого ґрунтується на уявленнях про енергетичну і геометричну неоднорідність поверхні. Характеристики поверхневої неоднорідності в науці про поверхню – ключова проблема, особливо коли мова заходить про кількісні критерії. Зокрема, найпростіший підхід зводиться до розгляду геометричної неоднорідності поверхні, тобто її відхилення від абсолютно плоскої. Однак, використання методів класичної хімії з цією метою пов’язане з великими труднощами, бо поверхнева неоднорідність визначається багатьма чинниками, які важко врахувати на практиці.
Концепція фрактальної розмірності може бути з успіхом використана для характеристики неоднорідності складних поверхонь. Ступінь нерегулярності поверхні задається фрактальною розмірністю Dfr,s, яка набуває значень між 2 і 3. Чим вища фрактальна розмірність поверхні, тим більше вона відрізняється від ідеально плоскої, тобто є більш шершавою. Фрактальну розмірність поверхні можна визначати, зокрема, адсорбційним і електрохімічним методами. Зупинимося на них детальніше.
Аналіз адсорбційних даних проводять декількома методами. Зокрема, кількість адсорбованих молекул в моношарі, виражена через об’єм газу Vg при стандартній температурі і тиску, залежить від площі поперечного перерізу частинок адсорбату σ*. в цьому випадку фрактальну розмірність визначають із співвідношення
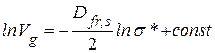 . .
| (1.111) |
В іншому методі для набору матеріалів одного виду, але з різними розмірами частинок, площа питомої поверхні sg визначається як деяка функція від діаметру частинок адсорбату d
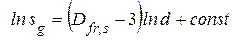 . .
| (1.112) |
Третій різновид визначення фрактальної розмірності поверхні грунтується на використанні модифікованої ізотерми адсорбції Френкеля-Гаслі-Хілла, яка описується рівнянням [42]
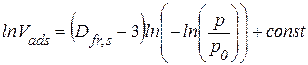 . .
| (1.113) |
Тут Vads – адсорбційний об’єм адсорбата при стандартних температурі і тиску, а р / р0 – відносний тиск. З рівняння (1.113) видно, що фрактальну розмірність поверхні Dfr,s можна визначити з нахилу логарифмічної залежності адсорбційного об’єму від відносного тиску. Рівняння (1.113) було використане для визначення фрактальної розмірності поверхонь кристалічних модифікацій TiO2 (анатазу і рутилу) і їх співіснуючих фаз, синтезованих золь-гелевим методом з наступною термічною обробкою [43]. Виявлено, що фрактальна розмірність залежить від типу кристалічної структури і не залежить від температурної обробки в межах того самого кристалічного типу. З трьох досліджених типів кристалічних структур найвищою фрактальною розмірністю характеризується рутильна модифікація, що свідчить про найбільшу нерегулярність її поверхні.
В електрохімічних системах як поверхню електрода, так, власне, й електрохімічну реакцію теж можна розглядати з точки зору їх фрактальності. Для визначення фрактальної розмірності поверхні електрода можна скористатися хроноамперометричним методом. В його основі лежить визначення дифузії електроактивних речовин до поверхні електрода, наприклад компонентів редокс-пари [Fe(CN)6]3–/[Fe(CN6)]4–. Для плоских електродів дифузія контролюється струмом і виражається показниковою залежністю у вигляді рівняння Коттрела [44]
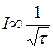 . .
| (1.114) |
Для шершавих реальних електродів це рівняння можна модифікувати до вигляду
 , ,
| (1.115) |
де σF – коефіцієнт пропорційності. Це означає, що в заданому проміжку часу струм виражається ступеневою залежністю від часу, а фрактальна розмірність входить в показник ступеня
 . .
| (1.116) |
Звідси видно, що фрактальну розмірність можна визначити з нахилу прямої, побудованої в логарифмічних координатах lg І – lg t (рис. 1.42). Для золотого електроосадженого електрода функціональний тангенс кута нахилу дорівнює 0,295, що відповідає фрактальній розмірності 1,590.

Рис. 1.42. Електрохімічне визначення фрактальної розмірності електроосадженого золотого електрода
1.5.6. Фрактальність процесів
На прикладі електрокаталітичного окиснення метану і карбон (ІІ) оксиду, а також електрохімічного відновленя кисню на платиновому електроді показано, що поза фрактальною розмірністю поверхні електрода можна визначити фрактальність електрохімічної реакції [45]. Знайдено, що фрактальні розмірності окиснення СН3ОН, СО і відновлення О2 менші двох і дорівнюють 1,817, 1,915 та 1,879 відповідно. Менша за 2 розмірність, очевидно, є свідченням того, що не вся двовимірна поверхня приймає участь в каталітичній реакції, тобто, що не всі каталітичні центри задіяні.

а б в
Рис. 1.43. Аналіз фрактального МАС-зображення поліпептиду (див. текст) [46]
Пептиди, ДНК, РНК, ензими, віруси, їхні комплекси і агрегати - типові природні фрактали. Тож методологію фракталів широко використовують для опису їх морфології, а також процесів взаємодії. Фрактальну природу осадженого на поверхню слюди пептиду можна спостерігати на МАС-зображеннях (рис. 1.43). Аналізом зображення була визначена фрактальна розмірність за допомогою формули
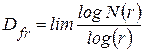 . .
| (1.117) |
Тут r – довжина фрагмента, а N(r) – розмір геометричного об’єкта, виміряний за допомогою масштабу r. Визначення фрактальної розмірності показано на (рис. 1.43, а–б). N розраховують як cуму кількості повних кроків між початковою А і кінцевою В точками та залишкової відстані. Наприклад, для зображення, представленого на рис. 1.43, а, r = 0,9 мкм. Для того щоб перейти від початкової точки А до кінцевої В вздовж контуру потрібно зробити 28 кроків. Залишкова відстань становить 0,64 мкм, що дає фрактальну довжину відносно r рівну 0,64 / 0,9 = 0,576. Звідси загальна довжина становить 28,576. Для фрактала, зображеного рис. 1.43, б, r = 1,8 мкм, а загальна довжина контура N = 10,38. Слід зазначити, що величина N залежить від місця стартової точки контура. На практиці користуються спрощеною теоремою Найквіста, згідно з якою вимірювання проводять з декількома різними стартовими точками з наступним усередненням [47]. Графічна залежність log N від log r (рис. 1.43, в) є прямою, з кута нахилу якої можна безпосередньо визначити фрактальну розмірність Dfr, яка для поліпептиду (рис. 1.43) становить 1,34.
Зручним і надійним методом дослідження біомолекулярної взаємодії служать сенсорні пристрої. До поширених типів біосенсорних пристроїв відноситься біосенсор, що працює на принципі резонансу поверхневих плазмонів. Донедавна вважалось, що рецептори рівномірно розподілені на поверхні сенсора, а значить для цього випадку придатна класична модель насичення процесу зв’язування аналіту з рецептором при умові, що лімітуючою стадією є дифузія частинок аналіту. Однак при ретельнішому аналізі експериментальних даних з’ясувалось, що поверхня біосенсора гетерогенна і для аналізу процесів зв’язування і дисоціації необхідна більш адекватна модель. При перегляді підходів до процесів зв’язування виходили з того, що ступінь гетерогенності поверхні біосенсора характеризується фрактальною розмірністю [48]. Це означає, що чим більша гетерогенність поверхні, тим більша фрактальна розмірність, тобто, невизначеність терміну гетерогенність замінюється кількісною характеристикою – нецілочисельною фрактальною розмірністю.
Нехай частинки аналіту (An) дифундують з розчину до поверхні, яка покрита частинками рецептора Rc, і при цьому утворюється комплекс (Rc·An). Кількість утворених комплексів визначається тривалістю взаємодії, що можна виразити співвідношенням
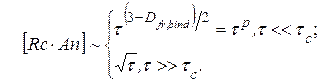
| (1.118) |
Тут Df,bind – фрактальна розмірність поверхні на стадії зв’язування; tc – час повного зв’язування. З рівняння (1.118) випливає, що концентрація комплексу [Rc·An] в реакції Rc + An → Rc·An на твердій фрактальній поверхні для малих проміжків часу виражається як [Rc·An] ~ tp, де р = (3 – Dfr,bind) / 2, тоді, як для значних часових проміжків [Rc·An] ~ t1/2.
Дисоціація комплексу і дифузія продуктів дисоціації від поверхні у об’єм розчину виражається співвідношенням
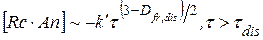 , ,
| (1.119) |
де Dfr,dis - фрактальна розмірність поверхні на стадії дисоціації; tdis – час початку процесу дисоціації.
Іноді на експериментальних кривих, що характеризують швидкість зв’язування, можна виділити дві прямолінійні ділянки. В цьому випадку адекватний опис експериментальних залежностей можливий шляхом так званого подвійного фрактального аналізу і визначенням чотирьох параметрів: k¢, k¢¢, D¢fr i D¢¢fr. Тоді для кількості комплексів (Rc·An) можна записати
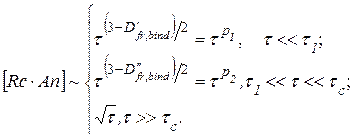
| (1.120) |
Слід зазначити, що фрактальна розмірність процесу зв’язування не є типовою незалежною змінною на зразок концентрації аналіту, якою можна безпосередньо маніпулювати. Вона визначається із рівнянь і її слід розглядати як залежну змінну. Фрактальність поверхні можна розглядати як міру шершавості, що зумовлює турбулентність потоків на ній, зменшення коефіцієнта дифузії і збільшення константи зв’язування і дисоціації.
Читайте також:
- IV. Проблема антропогенних змін клімату або «парниковий ефект».
- Аміноглікозиди (стрептоміцину сульфат, гентаміцину сульфат). Механізм і спектр протимікробної дії, застосування, побічні ефекти.
- Аналіз економічної ефективності капітальних вкладень
- Аналіз ефективності використання каналів розподілу
- Аналіз ефективності використання оборотних активів
- Аналіз ефективності використання основних засобів.
- Аналіз ефективності діяльності працівників банку
- Аналіз ефективності інвестиційних проектів
- Аналіз ефективності кредитних операцій
- Аналіз ефективності системи антиризикованих заходів
- Аналіз ефективності формування та використання банківських ресурсів
- Аналіз забезпеченості підприємства матеріальними ресурсами й ефективності їх використання.
Переглядів: 4186
| <== попередня сторінка | | | наступна сторінка ==> |
| Лекція №1 | | | Вплив температури на форму та розмір наночастинок |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |