• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Діаграма розсіювання регресійної функції

Рис. 1. Фактична залежність між у і х

Задача регресійного аналізу полягає в знаходженні оцінок α і β і, як наслідок, у визначенні прямої за точками А₁,А₂, ..., А_n.

Основні причини існування збурення:

1. Невключення в модель пояснювальних змінних.

2. Агрегування змінних.

3. Неправильний опис структури моделі.

4. Неправильна функціональна специфікація.

5. Помилки вимірювання.

Для аналізу залежності між двома змінними використовують діаграму розсіювання, яка є графічною формою представлення інформації у прямокутній системі координат.

Діаграма розсіювання є геометричною формою систематизації інформаційної бази процесу дослідження.

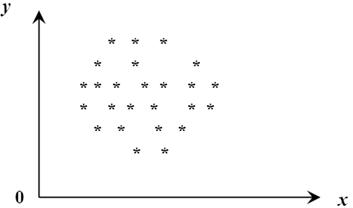
За шириною розкиду точок можна зробити висновок про тісноту зв’язку сукупності: якщо точки розміщені близько одна до одної (у вигляді вузької смужки), то можна стверджувати про наявність відносно тісного зв’язку; якщо точки на діаграмі розкидані широко, то має місце слабкий зв’язок між змінними

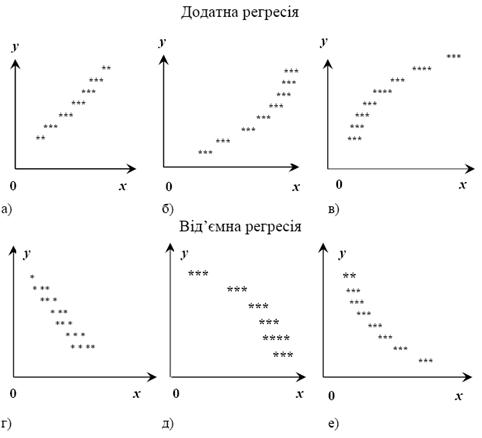
- кожному значенню пояснювальної змінної відповідає розподіл значень залежної змінної і навпаки;

- з’ясувати якою буде дія головних факторів-аргументів на залежну змінну, якщо б інші (другорядні, побічні) не змінювались і знаходились на одному й тому середньому рівні. Для цього визначають функцію регресії у вигляді математичного рівняннятого чи іншого вигляду.

Процес знаходження функції регресії називають вирівнюванням окремих значень залежної змінної.

Побудова регресії та визначення впливу пояснювальних змінних на залежну змінну – друга задача регресійного аналізу.

Припустимо, що за виглядом діаграми розсіювання встановимо лінійний характер залежності усереднених значень результативної змінної. Ця залежність опишемо за допомогою оціночної функції лінійної регресії:

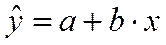, (2)

де a та b відповідно є оцінками параметрів α та β рівняння (1).

Знак «^» над у означає оцінку залежної змінної, отриману з рівняння (2) при деяких усереднених умовах.

Під простою регресією розуміється одностороння стохастична залежність результативної змінної від однієї пояснювальної змінної.

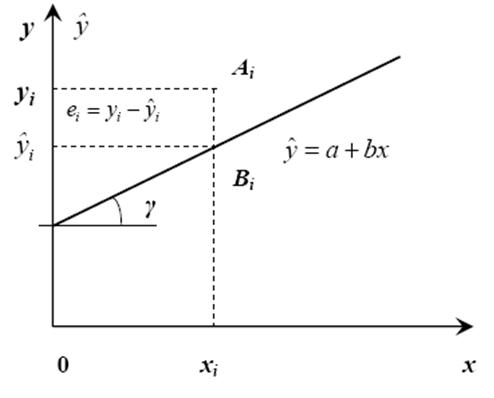
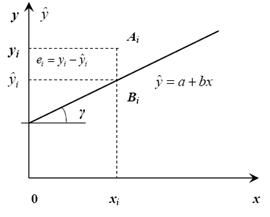
Рис. 4. Регресійна пряма та її параметри

При лінійній функції сукупність розрахункових значень утворює пряму регресії.

Значення функції регресії 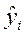таким чином є оцінками середніх значень змінної у для кожного фіксованого значення змінної х.

- економічна інтерпретація 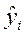: значення регресії 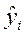показують середнє значення залежної змінної у при заданому х_і пояснювальної змінної у припущенні, що єдиною причиною зміни у є змінна х, а випадкова збурена змінна u набула значення, рівне нулю.

- чим менше значення е_і, тим більш вдало вибрана пряма.

3. Метод найменших квадратів

- зведення до мінімуму помилок специфікації форм зв’язку між змінними. Ці помилки визначаються через відхилення емпіричних даних 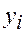від значень регресії 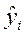, тобто вони формують значення збуреної змінної .

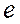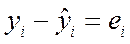(3)

Вимога: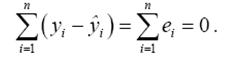(4)

- означає, що сума додатних відхилень повинна бути рівною сумі від’ємних.

Рис. 5. Пучок регресійних прямих (через координату ( хі; уі))

Вибіркова дисперсія – характеризує міру розсіювання дослідних значень 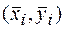довкола значень регресії, тобто дисперсію залишків е_і (залишкову дисперсію):

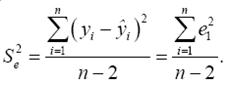(5)

Ступень вільності v: v=n–m–1,

де n – обсяг вибірки; m – число параметрів регресії.

- для простої лінійної регресії існує тільки одна пояснювальна змінна (m=1), то число ступенів вільності буде: v=n–1–1 = n–2.

Врахування числа ступенів вільності дає можливість отримати незміщену оцінку дисперсії.

Корінь квадратний із виразу (5) є стандартною помилкою оцінки регресії.

Вимогу про те, що міра розсіювання дослідних точок від гіпотетичної лінії повинна бути мінімальною з врахуванням (5), можна представити таким чином:

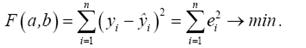(6)

- тобто сума квадратів відхилень емпіричних значень змінної у від значень, обчислених за рівнянням прямої, повинна бути мінімальною.

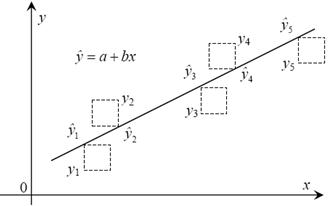Рис. 6. Графічне представлення МНК

Читайте також:

1. Pv– діаграма водяної пари
2. Адвокатура в Україні: основні завдання і функції
3. Алгоритм знаходження ДДНФ (ДКНФ) для даної булевої функції
4. Але відмінні від значення функції в точці або значення не існує, то точка називається точкою усувного розриву функції .
5. Аналіз коефіцієнтів цільової функції
6. АРХІВНІ ДОВІДНИКИ В СИСТЕМІ НДА: ФУНКЦІЇ ТА СТРУКТУРА
7. Асимптоти графіка функції
8. Асортиментний процес включає три основних етапи: концентрацію, кастомізацію і розсіювання.
9. Базальні ядра, їх функції, симптоми ураження
10. Базові функції, логічні функції
11. Банки як провідні суб’єкти фінансового посередництва. Функції банків.
12. Банківська система та її основні функції

Переглядів: 4852