• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Модель ближнього просторового перенесення

Лекція №5,6

Вітрові потоки повітря переносять в атмосфері забруднювальні речовини з урахуванням їх дрібномасштабних флуктуацій. Усередині потік субстанцій, що переносяться повітряними масами, має зазвичай адвективну та конвективну складові, а їх усереднені флуктуаційні рухи можна інтерпретувати як дифузію на фоні усередненого руху.

Нехай 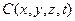– інтенсивність забруднення, поширюваного разом із потоком повітря в атмосфері; 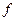– потужність джерел (стоків) забруднення; 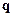- питомий потік маси домішок.

Будуючи математичну модель перенесення забруднень, будемо використовувати ейлерову балансову модель для довільного контрольного об’єму з межею 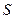. Тоді рівняння збереження маси в об’ємі можна записати в інтегральній формі

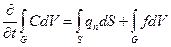, 4

де 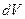– елемент об’єму, 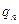– проекція питомого потоку маси 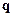на зовнішню нормаль.

Скориставшись теоремою Остроградського-Гаусса, перепишемо співвідношення у вигляді

,

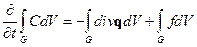звідки маємо

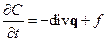. 5

Співвідношення (5) вказує що локальна зміна маси домішок у фіксованому об’ємі зумовлена дивергенцією сумарного потоку домішок

Потік концентрації домішок ураховує дифузійне та конвективне перенесення

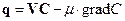6

де 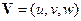- швидкість повітряних мас середовища; 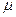- тензор вихрової, турбулентної дифузії, який для ортотропного середовища можна звести до діагональної форми.

Підставивши праву частину співвідношення (6) в (5), отримаємо диференціальне рівняння перенесення забруднення в атмосфері

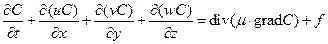7

де 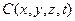- концентрація забруднювальної речовини в одиниці об’єму повітря; 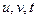- компоненти вектора швидкості повітряного середовища в декартовій системі координат 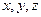(площина 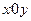відповідає земній поверхні); 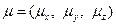- коефіцієнти турбулентної дифузії; 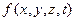- функція що характеризує джерела забруднення в просторі та часі.

Надалі розглянемо забруднення двох типів: аерозольні та дрібнодисперсні пилоподібні. Аерозольні забруднення розповсюджуються зі швидкістю частинок повітря. Пилові забруднення можуть переноситися в горизонтальному напрямку з горизонтальною швидкістю повітряної маси з урахуванням дії гравітаційних сил на частинки пилу.

Отже, аерозольні забруднення переміщуються зі швидкістю мас повітря, а пилоподібні забруднення переміщуються з частинками повітря та одночасно осідають зі швидкістю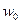

Рівняння (7) враховує як конвективне перенесення забруднення в просторі, так і турбулентне дифузійне перенесення, спричинене турбулентним характером течій повітря в атмосфері.

У рівнянні (7) можна врахувати взаємодію забруднення із середовищем. Найпростішою моделлю розпаду та хімічної нейтралізації забруднювальних речовин є реакція типу радіоактивного розпаду з коефіцієнтом .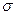

Форма підстилаючої поверхні також впливає на поширення домішок, у першу чергу на розподіл і напрямок руху повітряних мас поблизу поверхні Землі. Такі дані про структуру течії повітря з урахуванням рельєфу місцевості є вихідними даними гідрометеослужби.

Припустімо, що підстилаючи поверхня моделюється площиною 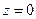, а вплив її форми враховується полем вектора швидкостей переміщення повітряних мас 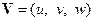. При цьому дані про поле швидкостей течії повітря є зовнішніми вихідними даними математичної моделі.

Місцеположення викидів забруднення та характер їх розміщення в просторі описується функцією 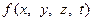. Розподілені в просторі джерела забруднення доцільно замінити системою точкових джерел у вигляді дельта функції Дірака, зберігаючи сумарне значення витрати. Завдяки цьому забезпечується простота і універсальність опису різних за фізичним змістом типів викидів та їх включення у комп’ютерну модель. Слід також мати на увазі, що для області з характерним розміром у декілька кілометрів велику кількість викидів (димові труби, запилені ділянки цехів тощо) доцільно моделювати точковими джерелами заданої інтенсивності.

Розглянуті вище фізичні механізми перенесення та викидів забруднювальних величин можна описати за допомогою диференціального рівняння

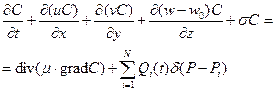8

де 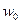– швидкість гравітаційного осідання частинок забруднюючих речовин; 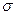– коефіцієнт розпаду (хімічного розкладання домішок), враховує зміну концентрації домішок із часом; 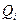– інтенсивність точкових джерел забруднення; 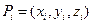- декартові координати місцеположення точкових джерел забруднення; 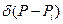- дельта-функція Дірака. За умови сталої за просторовими координатами концентрації (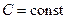) у диференціальному рівнянні (8), якщо немає джерел викидів і розпаду домішок, має бути розв’язок вигляду 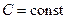, тобто маса домішок зберігається у разі довільного конвективного перенесення. Звідси випливає умова нерозривності, яку задовольняє поле швидкостей повітряної маси:

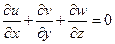. 9

Для визначення незалежних параметрів диференціальної задачі рівняння 8 доцільно записати у безрозмірному вигляді. Для цього розглянемо характерні розмірні величини:

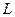- (м) – характерний розмір розрахункової області;

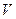- (м/с) - характерна швидкість повітряного потоку в регіоні (наприклад, максимальна швидкість вітру);

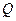- (кг/с) - потужність викиду точкового джерела з максимальною інтенсивністю.

З урахуванням прийнятих масштабів безрозмірні значення параметрів рівняння 8, позначені символом «~», такі:

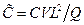- - концентрація забруднювальної речовини в одиниці об’єму;

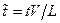- - час;

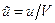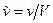- , , - компоненти вектора швидкості повітряного середовища;

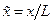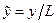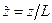- , , - декартові координати;

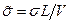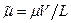- , - безрозмірні величини.

Зазначимо, що у безрозмірному вигляді диференціальне рівняння (8) не змінюється, замість розмірних величин тепер використовують відповідні безрозмірні аналоги.

Диференціальне рівняння (8) описує розсіювання забруднень у просторовій області , обмеженій земною поверхнею 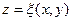і верхньою межею можливого вертикального поширення забруднення 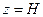, де вертикальна швидкість повітряного потоку .

На першому етапі математичного моделювання просторового перенесення забруднюючих речовин можна не враховувати рельєф місцевості чи враховувати його побічно, задаючи реальні для досліджуваної території значення швидкості руху повітряного потоку. При цьому компоненти вектора швидкості мають обов’язково задовольняти умову (9).

Отже, в області 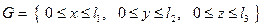будемо розглядати рівняння (8) з відповідними початковими та граничними умовами.

Розглянемо деякі варіанти початкових і граничних умов.

На бічних гранях області для 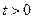обирають такі граничні умови, що моделюють процеси втікання чи витікання забруднення. На частині межі 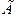, де повітряні маси втікають у розрахункову область, можна вважати, що концентрація забруднення С відома. Найчастіше забруднення, що втікає в , не враховують тому на межі 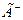(ділянці межі 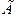, де 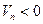)ставлять умову

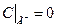10

Тут 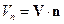- проекція вектора швидкості течії повітря на нормаль; - одиничний вектор зовнішньої нормалі до межі .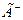

Коли повітряні маси на межі витікають з області . дифузійними перенесеннями нехтують порівняно з конвективними, тобто припускають що

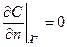
де 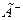- частина межі, де .

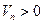На площині 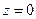задають умову третього роду 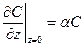, , 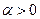де коефіцієнт 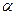враховує характер взаємодії забруднювальної речовини з підстилаючою поверхнею.

На верхній межі вертикальна складова вектора швидкості повітря 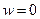, тобто виконується умова, яка означає, що немає дифузійного перенесення:

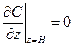
або

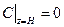
Якщо під час розповсюдження забруднення потрібно врахувати певну кількість субстанції що втікає, то умова (10) набирає вигляду

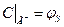, якщо .

Якщо викидів немає, початкова умова для рівняння (8) має вигляд

.

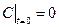Для задач розсіювання початкового викиду використовують умову

.

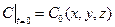Тривимірне диференціальне рівняння з частинними похідними використовують для математичного моделювання перенесення забруднень в атмосфері ближньої від джерел викидів області розміром до десятків кілометрів: в атмосфері міст, промислових зон тощо. Висота розповсюдження газового і пилового забруднень обмежена характерною висотою хмарності і становить менше 1…2 км.

Щоб реалізувати математичну модель, потрібно мати вхідні дані. Швидкість і напрямки повітряних мас для кожного регіону визначають на основі бази даних спостережень за різні проміжки часу (сезон, рік, місяць). При цьому обов’язкове виконання умови (9). Коефіцієнт 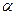враховує зміну з часом інтенсивності забруднення внаслідок дії різних факторів:

- хімічні перетворення забруднюючих речовин у випадку реакцій із зовнішнім середовищем;

- вимивання частинок забруднюючих речовин опадами.

Швидкості гравітаційного осідання частинок забруднення 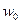залежать від багатьох факторів. Наведемо деякі емпіричні дані, які використовують у розрахунках:

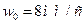- - для сполук сірки;

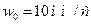- - для спор рослин і грибків;

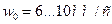- - для осколкових радіоактивних продуктів.

У розрахунках приземних концентрацій потрібно враховувати емпіричні залежності для коефіцієнтів турбулентної дифузії. Зазвичай для вертикального компонента тензора дифузії 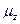використовують моделі у вигляді степеневої або лінійної залежності 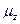від висоти.

Методологію моделювання поширення забруднення за певний період 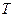на основі вхідної інформації можна подати так. Нехай для регіону, де розміщене джерело забруднення, впродовж періоду 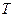відбувається 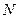метеорологічних ситуацій тривалістю .

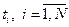Тоді, нехтуючи перехідними процесами, загальний процес розповсюдження забруднень за період 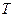можна вважати квазістаціонарним, тобто таким, що складається з стаціонарних метеорологічних ситуацій різних типів. Математичне прогнозування зводиться до послідовного розв’язування рівняння виду (8) із набором вхідних даних, які характеризують метеорологічний режим кожної ситуації. Потім значення концентрації 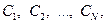, характерні для метеорологічних ситуацій тривалістю 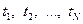, усереднюють:

.

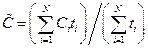У результаті отримують прогнозну оцінку про середній за період 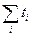розподіл забруднення в регіоні.

Кількість забруднення, що осіло на земну поверхню за проміжок 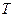, визначають за формулою

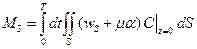
де 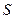- задана ділянка досліджуваного регіону.

Читайте також:

1. G2G-модель електронного уряду
2. OSI - Базова Еталонна модель взаємодії відкритих систем
3. Абстрактна модель
4. Абстрактна модель
5. Абстрактна модель оптимального планування виробництва
6. Американська модель соціальної відповідальності
7. Англійський економіст У. Бріджез пропонує модель організаційних змін за такими напрямками.
8. Англо-американська модель
9. Англо-американська модель
10. Багатомірна лінійна модель регресії.
11. Багатосегментна модель
12. Багатоцільова багатокритеріальна модель обґрунтування рішень в полі кількох інформаційних ситуацій

Переглядів: 761