
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Приклад розв’язання задачі 14
Задача 14. Розрахунок вала на витривалість при згині та крученні
Завдання до розрахунково-графічної роботи
Ступінчатий вал обертається на двох шарикопідшипниках (рис 6.1), на вал діє сила Р та циклічні скручувальні моменти Т з коефіцієнтом асиметрії r.
Якість поверхні характеризується величиною шорсткості.
Потрібно:
1. Показати розрахункову схему вала.
2. Побудувати епюри згинальних моментів та визначити небезпечні перерізи.
3. Розрахувати згинаючі моменти в небезпечних перерізах.
4. З умови міцності при згині і крученні визначити [P] (допустиму величину сили P).
5. Розрахувати коефіцієнт запасу вала.
Дані взяті з табл. 6.1.
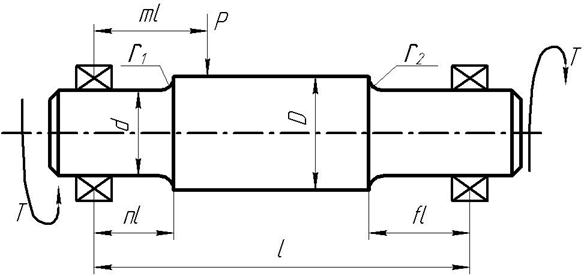
Рис. 6.6. Схема до виконання задачі 14
Таблиця 6.1
| № Варіанта | Матеріал | [nσ], [nτ] | r | Шорсткість Ra , мм | |
| Сталь 35 | 2,2 | -0,7 | 1,25 | ||
| Сталь 30 | 2,1 | -0,8 | 2,3 | ||
| Сталь 10 | 2,4 | -0,6 | 0,32 | ||
| Сталь 45 | 2,3 | -0,4 | 0,16 | ||
| Сталь 50 | 2,7 | -0,3 | 2,5 | ||
| 30ХМ | 2,8 | 0,4 | 1,26 | ||
| 40Х | 2,9 | 0,5 | 0,32 | ||
| 12ХН3А | 2,6 | 0,4 | 0,63 | ||
| 30ХГСА | 3,0 | 0,7 | 0,16 | ||
| 40ХНМА | 2,9 | 0,6 | 0,32 |
Таблиця 6.2
Дані геометрії вала (схеми 00, 01 ... 14)
За даними самостійно зобразити рисунок в масштабі
| № рисунка | l | a | m | n | f | d | D | r1 | r2 |
| см | мм | ||||||||
| 0,44 | 0,32 | 0,39 | |||||||
| 0,42 | 0,34 | 0,40 | |||||||
| 0,48 | 0,34 | 0,39 | |||||||
| 0,46 | 0,33 | 0,38 | |||||||
| 0,52 | 0,30 | 0,36 | |||||||
| 0,50 | 0,35 | 0,34 | |||||||
| 0,56 | 0,38 | 0,37 | |||||||
| 0,54 | 0,37 | 0,33 | |||||||
| 0,48 | 0,40 | 0,31 | |||||||
| 0,58 | 0,39 | 0,32 | |||||||
| 0,44 | 0,32 | 0,39 | |||||||
| 0,48 | 0,34 | 0,39 | |||||||
| 0,52 | 0,30 | 0,36 | |||||||
| 0,56 | 0,38 | 0,37 | |||||||
| 0,48 | 0,40 | 0,31 |
Дано:
матеріал – сталь 40ХН;

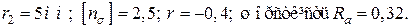
Розв’язування
Показники статичної і циклічної міцності сталі 40ХН (див. додатки В, Г)

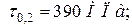
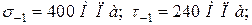
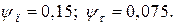
1. Знаходимо максимальну і мінімальну величини крутних моментів:
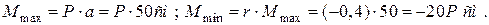
2. Креслимо розрахункову схему вала згідно з вихідними даними (рис. 6.1).
3. Будуємо епюри згинаючих моментів і визначаємо небезпечні перерізи вала.
4. Визначаємо опорні реакції (рис. 6.1).
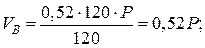
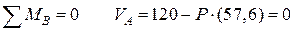
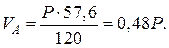
Перевірка:
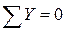 ,
, 
5. Визначаємо згинаючі моменти у характерних перерізах:
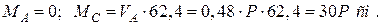
Будуємо епюру  (рис. 6.1). Крутні моменти по довжині вала однакові. Тому небезпечні перерізи визначаємо, орієнтуючись на розрахункову схему вала і епюру згинаючих моментів (рис. 6.2). Такими є перерізи С і Е , тому що за наявності концентраторів напружень у вигляді ступінчастої зміни діаметрів тут діють згинальні моменти, близькі до максимального.
(рис. 6.1). Крутні моменти по довжині вала однакові. Тому небезпечні перерізи визначаємо, орієнтуючись на розрахункову схему вала і епюру згинаючих моментів (рис. 6.2). Такими є перерізи С і Е , тому що за наявності концентраторів напружень у вигляді ступінчастої зміни діаметрів тут діють згинальні моменти, близькі до максимального.
6. Обчислення згинаючих моментів у небезпечних перерізах.
Переріз С:
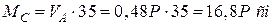
Переріз Е:

7. Визначимо  . Знаходимо
. Знаходимо 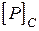 і
і 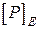 - величини допустимої сили для кожного перерізу. Менша з них і буде
- величини допустимої сили для кожного перерізу. Менша з них і буде  .
.
Переріз С
Знаходимо 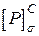 – допустиму величину сили Р з умови міцності при згинанні.
– допустиму величину сили Р з умови міцності при згинанні.
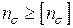
Нормальне напруження в небезпечній точці перерізу при обертанні вала змінюється за симетричним циклом. Тому коефіцієнт запасу обчислимо за формулою
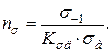
Амплітудне напруження 
Осьовий момент опору перерізу вала
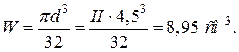 Тоді
Тоді
 .
.
Загальний коефіцієнт зниження границі витривалості деталі при симетричному циклі знайдемо за формулою:
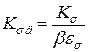 .
.
При 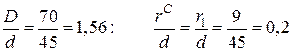 і
і  коефіцієнти концентрації напружень
коефіцієнти концентрації напружень 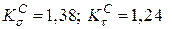 (див. додаток Д)
(див. додаток Д)  (див. додаток Е). При шорсткості
(див. додаток Е). При шорсткості 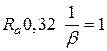 (додаток Ж)
(додаток Ж)
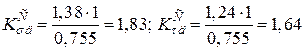
із (6.1) і (6.2) одержимо:


Розмірність: 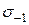 –
– 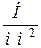 ,
, 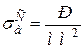 .
.
ІІ Знаходимо 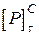 – допустиму величину сили Р з умови міцності при крученні
– допустиму величину сили Р з умови міцності при крученні

Матеріал у небезпечній точці сприймає асиметричний цикл дотичних напружень. Тому визначимо допустиме значення сили  з умови втомної міцності і сили
з умови втомної міцності і сили 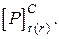 Записуємо умову втомної міцності
Записуємо умову втомної міцності 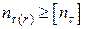 . Визначаємо коефіцієнт запасу
. Визначаємо коефіцієнт запасу 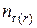 по відношенню до границі витривалості. Для цього обчислюємо добуток
по відношенню до границі витривалості. Для цього обчислюємо добуток 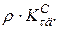 Характеристика
Характеристика 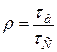 :
:
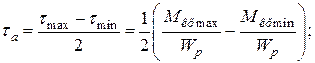
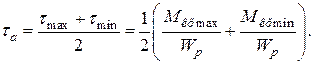
Полярний момент опору перерізу вала:
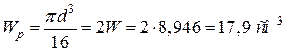
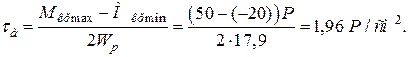
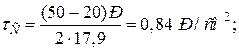
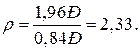
так як величина добутку 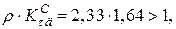 то для обчислення коефіцієнта запасу використовуємо формулу
то для обчислення коефіцієнта запасу використовуємо формулу

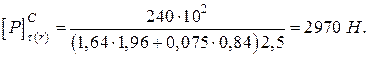
Розмірність: 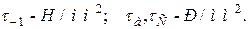
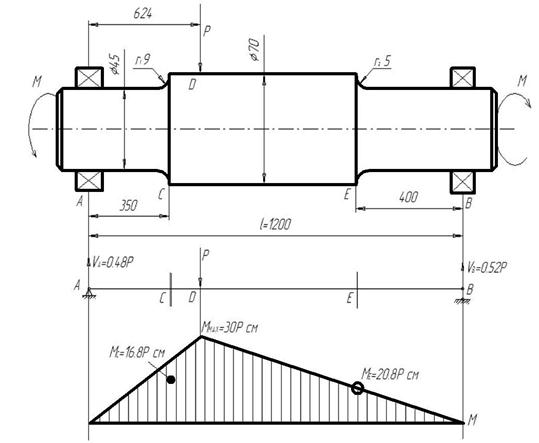
Рис. 6.7. Розрахункова схема вала
Знаходження 
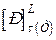 .
.
Записуємо умову статичної міцності
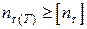 .
.
Коефіцієнт запасу по відношенню до границі текучості обчислюємо за формулою
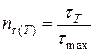 ,
,
де 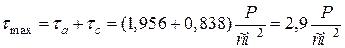 (6.15)
(6.15)
Враховуючи (6.13 - 6.15), одержимо
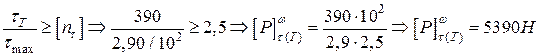 .
.
З порівняння величин
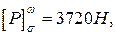
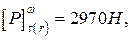
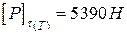 .
.
Робимо висновок, що для перерізу L допустима величина сили 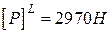 .
.
Переріз Е
1. Знаходимо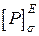
 .
.
Визначаємо коефіцієнти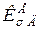 і
і 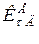 .
.
При  ,
, 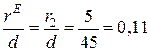 і
і 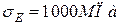 ,
,
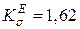 ,
, 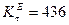 ,
, 
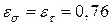 ; 1/β=1.
; 1/β=1.
Тоді 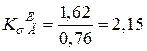 ;
; 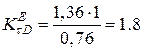
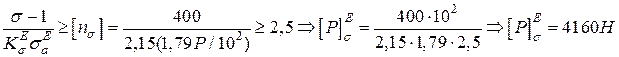 .
.
Розмірність  ,
,  .
.
Обчислюємо  при асиметричному крученні.
при асиметричному крученні.
Критерій 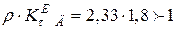 , і коефіцієнт запасу по відношенню до границі витривалості обчислюємо за формулою
, і коефіцієнт запасу по відношенню до границі витривалості обчислюємо за формулою
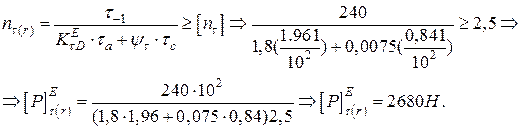
Амплітудні 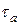 і середні
і середні 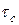 напруження в перерізах L і E однакові. Тому
напруження в перерізах L і E однакові. Тому
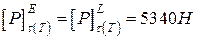 .
.
Як видно з порівняння 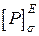 ,
,  і
і 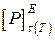 , для перерізу Е допустима величина сили
, для перерізу Е допустима величина сили 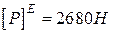 .
.
Отже, допустима величина сили Р для вала визначається втомою міцністю матеріалу в небезпечній точці перерізу Е.
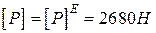 .
.
Обчислення коефіцієнта запасу міцності
При плоскому напруженому стані коефіцієнт запасу визначають за формулою
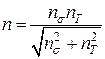 .
.
Обчислюємо n для кожного ймовірно небезпечного перерізу. Менша величина є коефіцієнтом запасу вала.
Коефіцієнт запасу  по нормальному напруженню обчислюється в небезпечній точці перерізів L і E .
по нормальному напруженню обчислюється в небезпечній точці перерізів L і E .
Переріз L
 ,
,
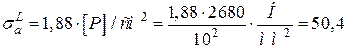 МПа.
МПа.
Тоді
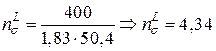 ,
,
 ,
,

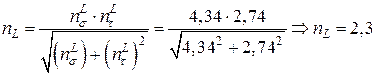 .
.
Переріз Е
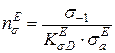 ,
,
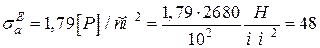 МПа.
МПа.
Тоді
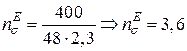 .
.
Оскільки величина  визначена з умови міцності матеріалу в небезпечній точці перерізу Е при крученні, то
визначена з умови міцності матеріалу в небезпечній точці перерізу Е при крученні, то
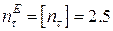 ;
; 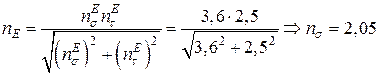 .
.
Значить, коефіцієнт запасу вала
 .
.
Відповідь: 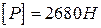 ; n = 2,05.
; n = 2,05.
Питання до захисту розрахунково-графічної роботи (задача 14)
1. Який порядок розрахунку вала на витривалість при згині та крученні?
2. Як знаходяться максимальні і мінімальні величини крутних моментів?
3. Як визначаються небезпечні перерізи?
4. Як визначається амплітудне навантаження?
5. Як знаходиться полярний момент опору перерізу вала?
6. Як обчислюється коефіцієнт запасу міцності?
7. Як визначається величина допустимого зусилля?
Читайте також:
- IV. Перевірка розв’язання і відповідь
- Абсолютні синоніми (наприклад, власне мовні й запозичені) в одному тексті ділового стилю вживати не рекомендується.
- Алгоритм однофакторного дисперсійного аналізу за Фішером. Приклад
- Алгоритм розв’язання задачі
- Алгоритм розв’язання розподільної задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі оптимізації в Excel
| <== попередня сторінка | | | наступна сторінка ==> |
| Розрахунок на міцність при повторно-змінних навантаженнях | | | Додаток Б |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |