• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Напруження і деформації при чистому зсуві

Чистим зсувом називається такий випадок плоского напруженого стану, при якому в околі досліджуваної точки можна виділити елементарний паралелепіпед на чотирьох бокових гранях якого будуть діяти тільки дотичні напруження (рисунок 5.2, а).

За формулами (3.6) і (3.7) знаходимо, що головні напруження при чистому зсуві дорівнюють

(5.2)

і діють на площадках, які складають кут 45^° з площадками дії t (рис. 5.2,б).

Рисунок 5.2	Деформацію при чистому зсуві характеризують такими величинами. Абсолютний зсув d - величина лінійного зміщення площадки зсуву (рисунок 5.3). Відносний зсув (або кут зсуву) (5.3)
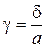Рисунок 5.3	де а - відстань між площадками, на яких діє дотичне напруження t і відносний зсув яких визначається. Відносний зсув g виражають в радіанах. Напруження і деформації при зсуві зв’язані між собою залежністю, яку називають закон Гука для зсуву. Закон Гука для зсуву справедливий лише в певних межах навантаження і записується у вигляді рівності

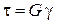(5.4)

Коефіцієнт пропорційності G характеризує жорсткість матеріалу (його здатність протидіяти пружним деформаціям) при зсуві. Його називають модулем зсуву або модулем пружності другого роду. Для сталі

G=8,1×10⁵ кг/см²=8,1×10¹⁰ Па=8,1×10⁴ МПа

Для ізотропних матеріалів між трьома пружними сталими E, m, i G існує залежність

(5.5)

При отримаємо .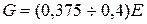

Запишемо вираз для переміщення однієї грані відносно іншої (для абсолютного зсуву 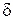) при чистому зсуві. Позначивши площу грані 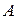, рівнодійну силу зсуву і відстань між гранями через 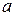(рисунок 5.3), отримаємо

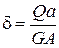(5.6)

Формула (5.6) виражає закон Гука при зсуві в абсолютних одиницях.

Потенціальна енергія деформації елемента при чистому зсуві

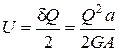, (5.7)

а питома потенціальна енергія

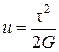. (5.8)

Читайте також:

1. IV. Критерій питомої потенціальної енергії деформації формозміни
2. Види деформації
3. Визначення втрат попереднього напруження
4. Визначення зусилля попереднього обтиску і величини попереднього напруження
5. Головні напруження та головні площадки.
6. Головні площадки і головні напруження
7. Деформації зсуву
8. Деформації при об’ємному напруженному стані. Узагальнений закон Гука
9. Деформації суцільного середовища
10. Для малих деформацій сила пружності пропорційна величині деформації і напрямлена в сторону, протилежну до зміщення частинок деформованого тіла
11. Допустиме напруження
12. Енергія пружної деформації

Переглядів: 937