
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Отже, сумою векторіві євектор , що сполучає початок вектораз кінцем вектораза умови, що векторвідкладено від кінця вектора.
Це правило називають правилом трикутника.
Для позначення операції додавання векторів вживають звичайні алгебраїчні символи:

Іншим способом побудови суми двох векторів є так зване правило паралелограма:якщо вектори  і
і  відкласти від спільного початку О (рис. 3) і на них побудувати паралелограм, то сума
відкласти від спільного початку О (рис. 3) і на них побудувати паралелограм, то сума 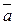 і
і  є вектор
є вектор  , що виходить з того ж початку О іспівпадає з діагоналлю паралелограма.
, що виходить з того ж початку О іспівпадає з діагоналлю паралелограма.

Рис. 3
З рис. З видно, що це правило є наслідком правила трикутника.
Розглядаючи фігури ОАС і ОВС (рис. 4), знайдемо, що
 , тобто сума двох векторів не залежить від порядку доданків.
, тобто сума двох векторів не залежить від порядку доданків.
 .
.
Послідовно використовуючи правило трикутника ми можемо побудувати суму будь-якого числа довільно розміщених у просторі векторів. Сумою цих векторів буде вектор, початком якого є початок першого вектора і кінцем - кінець останнього вектора - доданка.
Якщо кінець останнього вектора - доданка співпадає з початком першого, то сумою векторів буде нульовий вектор.
Різницею двох векторів 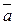 і
і  є вектор
є вектор 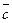 , що у сумі з вектором
, що у сумі з вектором  дає вектор
дає вектор  :
:
 якщо
якщо  .
.
З означення видно, що для побудови різниці  потрібно віднести вектори
потрібно віднести вектори  і
і  до спільного початку О (рис. 4) і провести вектор
до спільного початку О (рис. 4) і провести вектор

Рис. 4
 від кінця В вектора - від'ємника до кінця А вектора зменшуваного; цей вектор і є шукана різниця
від кінця В вектора - від'ємника до кінця А вектора зменшуваного; цей вектор і є шукана різниця  :
:
 .
.
Зауважимо, що у паралелограмі, побудованому на векторах 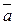 і
і  одна з діагоналей є сума векторів
одна з діагоналей є сума векторів 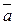 і
і  , а друга їх різниця (рис.4).
, а друга їх різниця (рис.4).
Добутком  вектора
вектора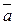 на число λ≠0є вектор:
на число λ≠0є вектор:
1)колінеарний вектору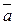 ,
,
2)модуль (довжина) якого дорівнює добутку 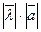 модулів числа λ і вектора
модулів числа λ і вектора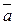 ;
;
3)напрям його співпадає з напрямом вектора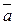 , якщо λ>0 або протилежний йому, якщо λ<0.
, якщо λ>0 або протилежний йому, якщо λ<0.
Ділення вектора на число просто звести до операції множення: щоб поділити вектор на число λ≠0, досить помножити цей вектор на обернене число  , тобто
, тобто

Зокрема, одиничний вектор, або орт 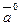 , відповідний вектору
, відповідний вектору 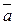 , дістанемо з вектора
, дістанемо з вектора 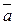 , поділивши останній на його модуль
, поділивши останній на його модуль  , тобто помноживши на
, тобто помноживши на  :
:

Добуток вектора на число має такі властивості:
1. 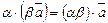 ,
,
2. 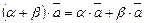 ,
,
3.  .
.
2. Виберемо у просторі довільну точку О. Будемо називати її початкомабо полюсом.Тоді положення будь-якої точки М простору можна однозначно визначити вектором  , початок якого є фіксована точка - полюс О, а кінець - точка М. Цей вектор називають радіус- вектор точкиМ відносно О і позначають
, початок якого є фіксована точка - полюс О, а кінець - точка М. Цей вектор називають радіус- вектор точкиМ відносно О і позначають 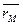 :
:

Рис. 5
Якщо задано дві точки М1 і М2, що визначають вектор 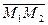 (рис.5), то
(рис.5), то  , тобто довільний вектор
, тобто довільний вектор 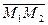 дорівнює різниці радіуса вектора його кінця і радіуса вектора його початку.
дорівнює різниці радіуса вектора його кінця і радіуса вектора його початку.
Розглянемо тепер задачу знаходження радіуса-вектора точки М, що лежить на прямій М1М2 і ділить відрізок у заданому відношенні λ (λ = М1 М: ММ2).
Очевидно, 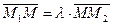 , але
, але 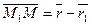 то
то 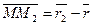 . Звідси
. Звідси
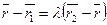
 (1.1)
(1.1)
В окремому випадку, коли М є середина відрізка  і формула (1.1) набуває вигляду
і формула (1.1) набуває вигляду
 (1.2)
(1.2)
3. Введемо тепер поняття про лінійну залежність векторів.
Вектори 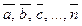 називають лінійно залежними,якщо існують такі числа α,β,γ,...,δ , з яких хоча б одне було відмінне від нуля, при яких лінійна комбінація цих векторів з коефіцієнтами α,β,γ,...,δ дорівнює нуль – вектору
називають лінійно залежними,якщо існують такі числа α,β,γ,...,δ , з яких хоча б одне було відмінне від нуля, при яких лінійна комбінація цих векторів з коефіцієнтами α,β,γ,...,δ дорівнює нуль – вектору
 .
.
Розглянемо спочатку два лінійно залежних вектори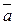 і
і  . З означення лінійної залежності маємо
. З означення лінійної залежності маємо
 , (1.3)
, (1.3)
при цьому, хоча б один з коефіцієнтів а і β, наприклад,а не дорівнює нулеві. Тоді знайдемо

Ця рівність означає, що вектори 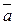 і
і  колінеарні.
колінеарні.
У випадку лінійної залежності трьох векторів маємо:
 (1.4)
(1.4)
Якщо а ≠0, то
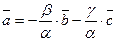
або

де
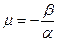 ,
,  .
.
Лінійна комбінація векторі 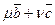 є вектор, що лежить у площині, в якій лежать вектори
є вектор, що лежить у площині, в якій лежать вектори 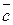 і
і  . Тому і рівний йому вектор
. Тому і рівний йому вектор 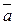 буде паралельний цій площині або лежати в ній. Отже, вектори
буде паралельний цій площині або лежати в ній. Отже, вектори 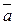 ,
,  ,
, 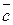 компланарні.
компланарні.
Це означає, що у випадку трьох компланарних векторів один з них можна розкласти за двома іншими неколінеарними векторами.
Дійсно, нехай маємо компланарні вектори 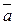 ,
,  ,
, 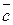 з яких
з яких 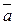 і
і  неколінеарні. Відкладаємо
неколінеарні. Відкладаємо  від спільного початку О (рис. 6) і позначимо
від спільного початку О (рис. 6) і позначимо  .
.
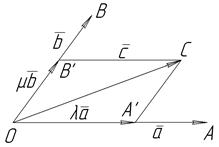
Рис. 6
Точки О,А,В,С знаходяться в одній площині. Через кінець С вектора 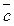 проведемо прямі СА' і СВ' паралельно прямим ОА і ОВ відповідно. Дістанемо паралелограм ОА'СВ', діагоналлю ОС якого є вектор
проведемо прямі СА' і СВ' паралельно прямим ОА і ОВ відповідно. Дістанемо паралелограм ОА'СВ', діагоналлю ОС якого є вектор 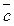 . Отже,
. Отже,

Вектори 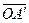 і
і 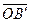 колінеарні векторам
колінеарні векторам  і
і  . Тому
. Тому

 де
де
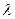 і
і  - відповідні відношення модулів цих пар колінеарних векторів.
- відповідні відношення модулів цих пар колінеарних векторів.
Звідси
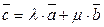 (1.5)
(1.5)
Покажемо тепер, що у випадку трьох некомпланарних векторів  ,
,  ,
, 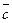 будь-який четвертий вектор
будь-який четвертий вектор  можна представити у вигляді
можна представити у вигляді
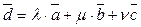 (1.6)
(1.6)
Для цього віднесемо вектори а,b,сі d до спільного початку О (рис. 7)
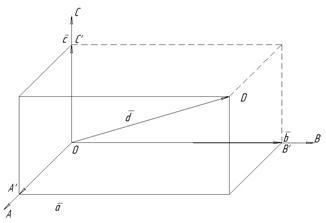
Рис. 7
і позначимо 
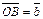 ,
,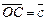 ,
,  . Через кінець D вектора
. Через кінець D вектора  проведемо площини паралельно площинам ОАВ, ОВС і ОСА. Отримаємо паралелепіпед, діагональ якого є вектор
проведемо площини паралельно площинам ОАВ, ОВС і ОСА. Отримаємо паралелепіпед, діагональ якого є вектор  , а ребра колінеарні відповідно векторам
, а ребра колінеарні відповідно векторам  ,
,  ,
, 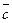 . Діагональ
. Діагональ 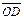 замикає ламану ОА'ND. Тому згідно з правилом додавання векторів маємо
замикає ламану ОА'ND. Тому згідно з правилом додавання векторів маємо

Оскільки  ;
;  ;
; колінеарні відповідно векторам
колінеарні відповідно векторам  ,
,  ,
, 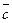 ., то, припустивши, що
., то, припустивши, що 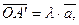 ,
, 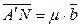 ,
,  , дістанемо шукану залежність:
, дістанемо шукану залежність:
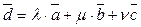
4. Координати на прямій.Розглянемо довільну пряму і виберемо на ній додатний напрям, фіксовану точку О (початок) і масштабну одиницю. Це - координатна вісь.
Координатну вісь можна також визначити віднесеним до її початку О одиничним вектором ї. Положення довільної точки М(r) на цій вісі

Рис. 8
визначимо її радіусом-вектором 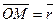 . Вектор
. Вектор  колінеарний орту
колінеарний орту  незалежно від положення точки М на вісі, а тому його завжди можна однозначно виразити через ірівністю
незалежно від положення точки М на вісі, а тому його завжди можна однозначно виразити через ірівністю

(1.6) де число х є відношення модулів колінеарних векторів 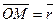 та
та  .Це число буде додатним (х>0), від'ємним (х<0) якщо ці напрями протилежні, і х= 0, якщо точка М співпадає з точкою О.
.Це число буде додатним (х>0), від'ємним (х<0) якщо ці напрями протилежні, і х= 0, якщо точка М співпадає з точкою О.
Рівність (1.6) встановлює взаємно однозначну відповідність між радіусом-вектором точок координатної вісі і дійсними числами.
Тому число г називають координатою вектора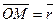 відносно базису(О;
відносно базису(О;  ). Положення точки М також буде визначено числом х- довжиною (модулем) вектора
). Положення точки М також буде визначено числом х- довжиною (модулем) вектора  . Це число називають координатою точкиМ і позначають М(х).
. Це число називають координатою точкиМ і позначають М(х).
Координати на площині.Щоб ввести поняття координат вектора і точки на площині побудуємо в ній так званий координатний базис. Для цього від довільно вибраної точки О в площині відкладемо упорядковану пару взаємно перпендикулярних одиничних векторів (ортів)  та
та  . Вектор і, що визначає координатну вісь Ох (вісь абсцис), розташуємо горизонтально і напрям його виберемо зліва направо, а вектор
. Вектор і, що визначає координатну вісь Ох (вісь абсцис), розташуємо горизонтально і напрям його виберемо зліва направо, а вектор  , що визначає координатну вісь Оу (вісь ординат),- вертикально і напрям його
, що визначає координатну вісь Оу (вісь ординат),- вертикально і напрям його

Рис.9
виберемо знизу вгору (рис. 9). Тепер кожний вектор площини, а отже і радіус - вектор  довільної точки М можна розкласти за базисними векторами
довільної точки М можна розкласти за базисними векторами  та
та  тобто представити у вигляді
тобто представити у вигляді
 (1.7)
(1.7)
З (1.7) видно, що кожному вектору площини відповідають два упорядкованих числа х і у - коефіцієнти при першому і другому базисних векторах, і навпаки, якщо задано два упорядкованих числа х і у, то можна однозначно побудувати відповідний їм вектор 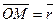 .
.
Числах іу називають координатами вектора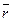 у вибраному базисі( О;i; j ).
у вибраному базисі( О;i; j ).
Положення довільної точки М на площині визначає її радіус - вектор  Тому кожній точці М можна поставити відповідну упорядковану пару чисел х і у. Ц\ числа називають координатами точкиМ і записують у вигляді М(х,у).
Тому кожній точці М можна поставити відповідну упорядковану пару чисел х і у. Ц\ числа називають координатами точкиМ і записують у вигляді М(х,у).
Координати у просторі.Назвемо координатним базисом у просторівіднесену до вибраної точки О (початок координат) упорядковану трійку перпендикулярних некомпланарних векторів  і
і  ,
,  . Орти
. Орти  і
і  лежать в горизонтальній площині і визначають відповідно вісь Ох- вісь абсцис і вісь Оу- вісь ординат. Орт
лежать в горизонтальній площині і визначають відповідно вісь Ох- вісь абсцис і вісь Оу- вісь ординат. Орт 
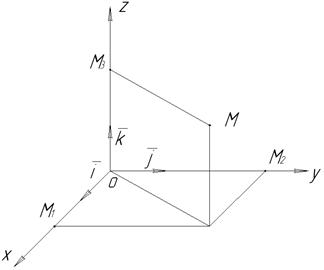
Рис. 10
проведено перпендикулярно до площини, в якій лежать орти  і
і  і визначає вісь Оz –вісь аплікат (додатний напрям
і визначає вісь Оz –вісь аплікат (додатний напрям  - вгору).
- вгору).
Кожна пара з трійки векторів визначає площину, яку називають координатна площина.
Всі точки координатної площини, що визначено ортами і
і  (площина Оуz), мають координату х-0, ортами
(площина Оуz), мають координату х-0, ортами  і
і  (площина Охz) - у = 0, а ортами
(площина Охz) - у = 0, а ортами  і
і  (площина Оху)- z = 0.
(площина Оху)- z = 0.
Розклад довільного вектора  за базисними векторами
за базисними векторами
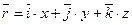 (1.8)
(1.8)
однозначно визначає для кожного вектора 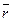 три упорядковані числа х, у, z - координати вектора
три упорядковані числа х, у, z - координати вектора у вибраному базисі
у вибраному базисі і
і  ,
,  .
.
Положення кожної точки М простору визначає ЇЇ радіус - вектор  .Цей вектор цілком визначено його координатами { х, у, z }. Тому і довільній точці М можна поставити взаємно однозначну відповідність упорядковану трійку чисел х, у, z, які будемо називати координатами точкиМ і записувати М{х, у, z).
.Цей вектор цілком визначено його координатами { х, у, z }. Тому і довільній точці М можна поставити взаємно однозначну відповідність упорядковану трійку чисел х, у, z, які будемо називати координатами точкиМ і записувати М{х, у, z).
5. Розглянемо тепер дії з векторами у координатній формі.
Якщо у просторі задано два вектори їх координатами
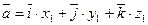

то на підставі алгебраїчних властивостей додавання, віднімання і множення вектора на число отримаємо
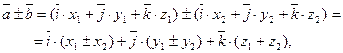 (1.9)
(1.9)
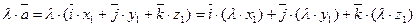 (1.10)
(1.10)
тобто, координати суми (різниці) двох векторів дорівнюють сумам (різницям) відповідних координат цих векторів,а координати добутку вектора на число дорівнюють добуткам відповідних координат вектора на це число.
Узагальненням цих результатів є правило знаходження координат лінійної комбінації векторів.
Якщо у просторі
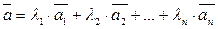 (1.11)
(1.11)
і 
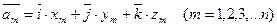 то
то
 (1.12)
(1.12)
Для площини формули, відповідні формулам (1.9) - (1.12), отримаємо, взявши координати z = 0, а для прямої -у=0, z =0.
Знайдемо координату точки М{х, у, z), що ділить відрізок М1М2 між точками М1 (х1; у1 ; z1 ) і М2(х2 ,у2, z 2) у відношенні  З формули (1.1)
З формули (1.1)
 (1.13)
(1.13)
маємо
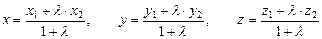 (1.14)
(1.14)
Як окремий випадок для 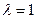 дістанемо формули, що визначають координати середини відрізкаМ1М2 :
дістанемо формули, що визначають координати середини відрізкаМ1М2 :

Тепер знайдемо координати х, у, zвектора 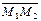 , початком якого є точка М1 (х1; у1 ; z1 ), а кінцем - точка М2(х2 ,у2, z 2). із-за того, що
, початком якого є точка М1 (х1; у1 ; z1 ), а кінцем - точка М2(х2 ,у2, z 2). із-за того, що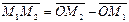 отримаємо
отримаємо
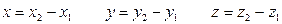 .
.
Як відомо, між колінеарними векторами 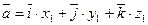
 існує лінійна залежність
існує лінійна залежність

Звідси
 або
або
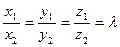 (1.15)
(1.15)
Це означає, що координати колінеарних векторів пропорційні між собою.
Між компланарними векторами 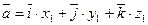 ,
,  існує лінійна залежність:
існує лінійна залежність:

Векторна рівність еквівалентна трьом різностям:

Ця система рівнянь відносно  лінійна і однорідна. А для того, щоб вона мала ненульовий розв'язок, необхідно і достатньо, щоб визначник системи дорівнював нулеві:
лінійна і однорідна. А для того, щоб вона мала ненульовий розв'язок, необхідно і достатньо, щоб визначник системи дорівнював нулеві:
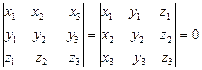
Отримана формула і дає ознаку того, що три вектори компланарні.
Підсумок заняття
Читайте також:
- Адміністративні зміни кінця 18-19 ст. та утворення нових архівів
- Академічна філософія кінця – XIX – поч. XX ст.
- Але, головним залишається діючий початок, чим повсякденність і відрізняється від фантазії (казки, міфу).
- Біомаса - Кількість живої речовини на одиниці площі чи об'єму місцеперебування в момент спостереження. Визначається сумою біомаси усіх популяцій, що населяють дану екосистему.
- Вересня 1939 р. Німеччина напала на Польщу, що поклало початок Другій світовій війні.
- Визначення допустимого часу початку долання зон радіоактивного забруднення (початок виходу із зони) при заданій дозі опромінення
- Визначення кінця титрування
- Випадок рівномірного розподілу на відрізку з фіксованим кінцем
- Відмінність дійового каяття від добровільної відмови від доведення злочину до кінця.
- Відповідно до ст. 69 ЦПК перебіг процесуального строку починається з наступного дня після відповідної календарної дати або настання події, з якою пов'язано його початок.
- Війна Радянської Росії проти УНР(кінець 1917 – початок 1918 рр. ). Причини поразок укр. військ.
- Встановлення радянської влади в Україні: передумови, причини, наслідки.
| <== попередня сторінка | | | наступна сторінка ==> |
| Вектори рівні, якщо вони колінеарні, мають однакові напрями і рівні модулі. | | | Контрольні питання |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |