• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Правила додавання швидкостей в релятивістській механіці

Постулати спеціальної теорії відносності (СТВ). Перетворення Лоренца

1. Швидкість світла і правило додавання швидкостей.

До середини XIX ст. швидкість світла була виміряна вже досить точно. Її значення у вакуумі складає 3·10⁸ м/с. Виникло питання про те, до якої інерціальної системи відноситься це значення швидкості. І виникло воно тому, що згідно з правилом додавання швидкостей у класичній фізиці

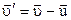. (1.82)

Швидкість руху, в тому числі і швидкість руху світла, в різних інерціональних системах відліку різна.

Експериментальні дослідження в цьому напрямі показали, що швидкість руху світла в різних інерціональних системах відліку однакова, що суперечить (1.82). Отже, перетворення Галілея, з яких слідує правило (1.82), мають обмежену область застосування; вони застосовні, коли .

І так виникла необхідність переглянути ті основні положення, які лежать в основі перетворень Галілея, зокрема положення про абсолютність простору і часу. Цю задачу в 1905 році розв’язав Ейнштейн.

2. Постулати СТВ.

За основу своєї теорії Ейнштейн вибрав два положення, які називають постулатами спеціальної теорії відносності:

1). В усіх інерціональних системах відліку всі фізичні явища (механічні, електричні, магнітні, оптичні) при одних і тих же умовах протікають однаково (принцип відносності).

2). Швидкість світла у вакуумі однакова в усіх інерціональних системах відліку і не залежить від руху джерела світла (принцип інваріантності швидкості світла).

3. Перетворення Лоренца.

Виходячи з цих положень, Ейнштейн показав, що зв’язок між координатами і часом у двох інерціональних системах відліку (і) виражається не перетвореннями Галілея, а перетвореннями Лоренца.

У випадку, коли координатні осі і систем відліку (і) співпадають, перетворення Лоренца мають вигляд:

; ; ;,

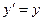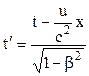де 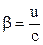(– відносна швидкість систем відліку; швидкість світла у вакуумі).

Звернемо увагу на першу і останню формули. Вони наочно вказують на те, що не тільки координата залежить від часу, але й час залежить від координати, тобто між простором і часом є взаємозв’язок. Координата і час залежать також від швидкості системи відліку, тобто властивості простору і часу залежать від характеру руху матеріальних об’єктів – простір і час є якостями існування матерії.

Дуже істотно, що при формули Лоренца переходять у формули перетворень Галілея, де маємо:

; ; ; .

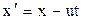§ 1.24. Властивості простору і часу в релятивістській механіці (наслідки із перетворень Лоренца)

1. Поняття одночасності подій. Нехай у системі в точках з координатами і 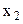в моменти часу 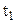і 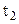відбуваються дві події. В системі , яка рухається відносно з швидкістю , вздовж осі , цим подіям відповідають координати і в моменти часу і .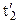

Якщо події в системі відбуваються в одній точці (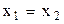) і є одночасними (), то згідно з перетвореннями Лоренца

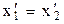і ,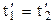

тобто ці події є одночасними і такими, що просторово збігаються для довільної інерціональної системи відліку.

Якщо події в системі просторово рознесені (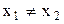), але одночасні (), то в системі

;,

;.

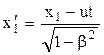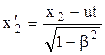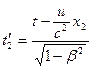Бачимо, що

і .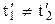

Отже, в системі ці події, залишаючись просторово рознесеними, виявляються неодночасними. Знак різниці 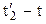визначається знаком виразу , тому в різних точках системи різниця буде неоднаковою за величиною і за знаком.

2. Відносність довжини. Нехай деяке тіло (наприклад, стержень), розміщене вздовж осі , рухається разом з системою відліку і має в цій системі довжину , де і – координати початку і кінця стержня.

За першою формулою перетворень Лоренца маємо

.

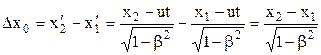Різниця – дає довжину стержня в системі .

Тоді або .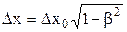

Оскільки , то .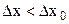

Отже, довжина стержня, яка виміряна в системі, відносно якої він рухається, є меншою від довжини, виміряної в системі, відносно якої стержень знаходиться у стані спокою. Лінійні розміри стержня в системі відліку, відносно якої він не рухається, є найбільшими. Ці найбільші розміри називають власними розмірами.

Зауважимо, що твердження про скорочення лінійних розмірів тіл у напрямі руху не означає якогось фізичного процесу в стержні, подібного деформації системи; мова йде про значення вимірювання стержня в різних системах відліку.

3. Відносність проміжку часу. Нехай у деякій точці, яка нерухома в системі , відбувається подія, тривалість якої .

За четвертою формулою перетворень Лоренца маємо

Різниця – дає тривалість події в системі . Різниця - дає зміщення точки, де відбувається подія, в системі відліку .

Тоді або . (1.83)

Оскільки , то .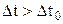

Отже, проміжок часу між двома подіями в різних інерціальних системах відліку різний; проміжок часу відносний. Він найменший в тій системі відліку, відносно якої точка, де відбувається подія, нерухома. Цей найменший проміжок часу називається власним часом.

Формула (1.83) знайшла своє експериментальне підтвердження. В космічних променях є такі елементарні частинки як – мезони. Ці частинки нестабільні – вони розпадаються на інші елементарні частинки. Час життя – мезонів, коли вони знаходяться у стані спокою, складає 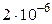с. За такий час, навіть рухаючись зі швидкістю світла, – мезони могли би пролетіти шлях 600 м. В той же час дослідження показують, що мезони утворюються на висоті 20-30 км. і встигають долетіти до Землі. Пояснюється це тим, що час 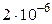с. це власний час життя мезонів, тобто час виміряний по годиннику, який рухається разом з частинкою. Час виміряний по годиннику в системі відліку, зв’язаною із Землею більший і частинка встигає пролетіти більшу відстань.

4. Поняття інтервалу між двома подіями. З назви теорії і її попередніх результатів може скластися хибна думка про те, що “все в світі відносне”. Насправді, теорія відносності точніше, ніж класична фізика, відображує поняття абсолютного і відносного в розвитку матеріального світу та його пізнанні.

З приводу СТВ Планк у свій час писав: “Її привабливість для мене полягає в тому, що я прагнув з усіх її положень вивести те абсолютне, інваріантне, що лежить в її основі”. І такі абсолютні, інваріантні величини були знайдені.

Взаємозв’язок між простором і часом показує, що для математичного відображення будь-якої події слід користуватися чотиривимірною системою відліку, де роль четвертої координати відіграє час. Точку в такій системі відліку, яка визначає певну подію, називають світовою точкою.

Розглянемо дві події. Нехай в системі відліку одна з них визначається координатами , а друга – координатами .

Величину 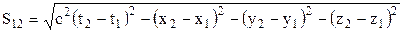називають інтервалом між двома подіями.

Неважко показати, що інтервал є інваріантом відносно перетворень Лоренца. Квадрат інтервалу в системі можна записати у вигляді

,

а відповідний квадрат інтервалу між двома подіями в системі

. (1.84)

Використавши формули

; ; ;

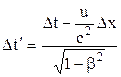
та підставивши їх у вираз (1.84), дістанемо .

Інтервал між подіями можна виразити через такі дві компоненти: квадрат просторової відстані

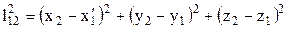та квадрат проміжку часу .

Тоді . (1.85)

З виразу (6.4) видно, що хоч обидві компоненти мають відносний характер, інтервал, як і швидкість світла, інваріантні відносно перетворень Лоренца. Останні в теорії відносності належать до абсолютних величин.

Спираючись на перетворення Лоренца, знайдемо зв’язок між швидкостями тіла в двох інерціальних системах відліку (і ). Розглянемо простий випадок, коли тіло рухається паралельно до осі (або

). Тоді ; ; 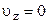, відповідно ; ; .

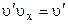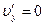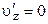За означенням швидкості , .

Продиференціюємо перше і четверте рівняння перетворень Лоренца

; .

Поділимо почленно ліві і праві частини отриманих рівнянь

.

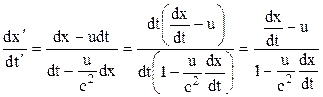Замінивши похідні відповідними компонентами швидкості, дістанемо

.

Отже, або .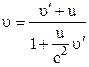

Отримані формули виражають правило додавання швидкостей в релятивістській механіці.

Нехай 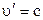і . Тоді

.

Бачимо, що результуюча швидкість 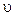не перевищує швидкості світла у вакуумі. Отже, швидкість світла у вакуумі є граничною швидкістю. І ніякі дослідні факти в сучасній фізиці не заперечують висновку про те, що швидкість світла у вакуумі є межею можливих швидкостей в природі.

Читайте також:

1. V. Етичні правила психологічних досліджень
2. А ви слідуєте цім правилам, коли виступаєте публічно?
3. Автододавання та автообчислення.
4. Аксіоми додавання і множення
5. Види графіків та правила їх побудови.
6. Визначення суми на множині цілих невід’ємних чисел, її існування та єдиність. Операція додавання та її основні властивості (закони).
7. ВИЗНАЧЕННЯ ШВИДКОСТЕЙ ЛАНОК
8. Визначення, класифікація і правила побудови індексів
9. Вимоги до керівника, правила та принцинципи управління
10. Відомості про правила охорони і техніки безпеки на підземних гірничих роботах.
11. Властивості простору і часу у класичній механіці
12. Воднеподібні атоми в квантовій механіці. Квантові числа

Переглядів: 3692