
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
ВИЗНАЧЕННЯ ШВИДКОСТЕЙ ЛАНОК
Лекція 4. Тема 2.2.
Планом швидкостей механізму називається векторна діаграма, на якій зображені у вигляді відрізків вектори, однакові по модулю і напрямку з швидкостями різних точок ланок механізму в даний момент часу.
Побудова планів швидкостей проводиться на основі послідовного складання векторних рівнянь для всіх груп, що входять до складу механізму, починаючи із ведучої ланки. Спочатку потрібно вибрати загальну для двох ланок точку та записати для неї два рівняння для визначення її швидкості. Для визначення повної картини швидкостей будь-якої ланки, що входить у групу, досить знати лінійну швидкість двох точок цієї ланки або лінійну швидкість однієї точки й кутову швидкість ланки.
У методі планів швидкостей і прискорень використовується теорема про складний рух твердого тіла, який можна представити як суму переносного та відносного руху (рис.2.3 а).
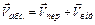
Переносний рух - рух рухомої системи відліку ( рис. 2.3.а) відносно нерухомої системи відліку (
рис. 2.3.а) відносно нерухомої системи відліку (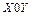 рис. 2.3.а). Відносний рух – рух матеріальної точки відносно рухомої системи відліку (на рис.2.3 а, рух точки А відносно системи координат
рис. 2.3.а). Відносний рух – рух матеріальної точки відносно рухомої системи відліку (на рис.2.3 а, рух точки А відносно системи координат  ). У будь-який момент часу можна знайти точку, жорстко пов'язану з тілом, швидкість якої дорівнює нулю. Це миттєвий центр обертання тіла або полюс
). У будь-який момент часу можна знайти точку, жорстко пов'язану з тілом, швидкість якої дорівнює нулю. Це миттєвий центр обертання тіла або полюс 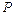 (рис. 2.3.б). Якщо тіло рухається поступально то миттєвий центр обертання лежить на
(рис. 2.3.б). Якщо тіло рухається поступально то миттєвий центр обертання лежить на  . Відносно цієї точки в даний момент часу тіло здійснює обертовий рух зі швидкістю
. Відносно цієї точки в даний момент часу тіло здійснює обертовий рух зі швидкістю 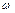 .
.

| 
| 
|
| а | б | в |
| Рис. 2.3 |
Перенесемо вектори абсолютних швидкостей  та
та 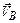 в точку
в точку  -полюс плану швидкостей (рис. 2.3 в).
-полюс плану швидкостей (рис. 2.3 в).
Одержимо план швидкості відрізка АВ у масштабі:
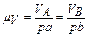
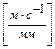
Для визначення швидкості точки С можна записати наступну систему:
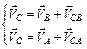 .
.
Припустимо, що ця швидкість відома, тоді
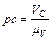 .
.
З іншого боку
 ;
;  ;
; 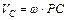
 або
або
 .
.
З'єднані між собою кінці векторів абсолютних швидкостей утворюють фігуру, подібну до ланки та повернену до неї на кут 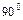 .
.
Властивості планів швидкостей:
1. Вектори, які виходять із полюса, є абсолютними швидкостями.
2. Напрямок вектора - завжди від полюса.
3. На кінці вектора завжди точка, що відповідає швидкості точки ланки або кінематичної пари.
4. Вектори на планах швидкостей, які не проходять через полюс, є відносними швидкостями.
5. Напрямок відносних швидкостей на плані завжди від другого індексу до першого.
Приклад побудови плана швидкостей (рис.2.4).
У довільній точці вибираємо полюс 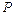 . Цій точці відповідають кінематичні пари з нульовою швидкістю
. Цій точці відповідають кінематичні пари з нульовою швидкістю  ,
,  і направляюча повзуна
і направляюча повзуна  .
.
Таким чином, для точки  можна записати рівняння
можна записати рівняння
 ,
,
де 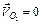 - швидкість точки
- швидкість точки  , а
, а 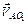 - швидкість точки
- швидкість точки  відносно точки
відносно точки  . У такий спосіб
. У такий спосіб
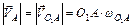 ,
,
вектор  направлений по дотичній до траєкторії руху точки
направлений по дотичній до траєкторії руху точки  , тобто перпендикулярно
, тобто перпендикулярно  , у бік обертання кривошипа. При цьому кутова швидкість кривошипа
, у бік обертання кривошипа. При цьому кутова швидкість кривошипа  визначається згідно залежності:
визначається згідно залежності:
 , [c-1]
, [c-1]
де  - частота обертання кривошипа
- частота обертання кривошипа  [хв-1]. Виходячи з вище сказаного, на плані швидкостей (рис. 1.2) будуємо пряму
[хв-1]. Виходячи з вище сказаного, на плані швидкостей (рис. 1.2) будуємо пряму 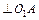 і на ній у масштабі відкладаємо точку
і на ній у масштабі відкладаємо точку  (
( ,
,  - масштабний коефіцієнт плану швидкостей), що відповідає швидкості точки
- масштабний коефіцієнт плану швидкостей), що відповідає швидкості точки  .
.
Для визначення швидкості точки 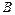 можна записати наступну систему:
можна записати наступну систему:
 ,
,
де 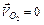 - швидкість точки
- швидкість точки  ,
, 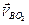 - швидкість точки
- швидкість точки 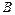 відносно
відносно  ,
, 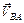 - швидкість точки
- швидкість точки 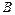 відносно
відносно  .
.
Кутові швидкості коромисла  і шатуна
і шатуна  нам не відомі, але нам відомі напрямки
нам не відомі, але нам відомі напрямки 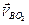 і
і 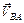 . Таким чином із полюса
. Таким чином із полюса 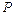 на плані швидкостей проводимо пряму
на плані швидкостей проводимо пряму 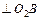 , а із точки
, а із точки  проводимо пряму
проводимо пряму  . На перетині цих двох прямих лежить точка
. На перетині цих двох прямих лежить точка 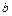 , що відповідає абсолютній швидкості точки
, що відповідає абсолютній швидкості точки 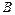 .
.
Використовуючи теорему подібності можна записати залежність:
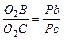 .
.
Із полюса 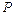 через точку
через точку 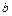 проводимо відрізок
проводимо відрізок  . Точка
. Точка  на плані швидкостей відповідає швидкості точки
на плані швидкостей відповідає швидкості точки 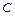 на плані положення механізму.
на плані положення механізму.
Повзун  робить лінійне переміщення вздовж вертикальних нерухомих направляючих по осі, що проходить через точки
робить лінійне переміщення вздовж вертикальних нерухомих направляючих по осі, що проходить через точки  і
і  . Для швидкості
. Для швидкості 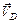 можна записати векторне рівняння:
можна записати векторне рівняння:
 ,
,
де  - швидкість точки
- швидкість точки 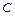 ,
, 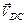 - швидкість точки
- швидкість точки  відносно
відносно 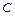 .
.
Із полюса 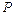 проводимо вертикальну пряму, паралельну до
проводимо вертикальну пряму, паралельну до 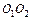 , а з точки
, а з точки  , на плані швидкостей, проводимо іншу пряму, перпендикулярну шатуну
, на плані швидкостей, проводимо іншу пряму, перпендикулярну шатуну  . На перетині цих прямих знаходиться точка, яка відповідає лінійній швидкості точки
. На перетині цих прямих знаходиться точка, яка відповідає лінійній швидкості точки  . А абсолютна величина
. А абсолютна величина
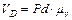 ,
,
де 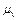 - масштаб плану швидкостей.
- масштаб плану швидкостей.
 
|
| Рис. 2.4 План швидкості |
Читайте також:
- I визначення впливу окремих факторів
- II. Визначення мети запровадження конкретної ВЕЗ з урахуванням її виду.
- II. Мотивація навчальної діяльності. Визначення теми і мети уроку
- Ocнoвнi визначення здоров'я
- Алгебраїчний спосіб визначення точки беззбитковості
- Аналіз службового призначення деталей та конструктивних елементів обладнання харчових виробництві, визначення технічних вимог і норм точності при їх виготовленні
- Аналіз стратегічних альтернатив та визначення оптимальної стратегії формування фінансових ресурсів
- Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
- Балансова теорія визначення статі. Диференціація статі і роль гормонів у цьому процесі.
- Безстатеве розмноження, його визначення та загальна характеристика. Спори — клітини безстатевого розмноження, способи утворення і типи спор.
- Біостратиграфічні методи визначення віку порід
- Біуретовий метод визначення білків
| <== попередня сторінка | | | наступна сторінка ==> |
| Аналітичний метод | | | ВИЗНАЧЕННЯ ПРИСКОРЕНЬ ЛАНОК |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |