• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Розрахунок електричних полів за допомогою теореми Остроградського-Гауса

Для розрахунку електричного поля створеного зарядженим тілом необхідно розбити це тіло на точкові заряди і визначити напруженість електричного поля в деякій точці простору за принципом суперпозиції. Для багатьох тіл такі розрахунки математично досить складні. Для деяких симетричних тіл розрахунок електричного поля значно спрощується при використанні теореми Остроградського-Гауса. Розглянемо деякі приклади таких розрахунків.

а) Електричне поле рівномірно зарядженої кулі.

Розглянемо кулю радіусом R рівномірно заряджену по об’єму з об’ємною густиною заряду

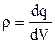. (3.27)

Для рівномірного розподілу заряду можна вважати що

. (3.28)

Оскільки об’єм кулі рівний

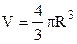, (3.29)

то підставивши (3.29) в (3.28) одержимо:

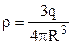. (3.30)

Виберемо замкнену поверхню S у формі сфери радіусом r, центр якої співпадає з центром зарядженої кулі, як зображено на рис. 3.5. Розглянемо випадок коли 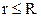, тобто визначимо напруженість електричного поля всередині зарядженої кулі. Запишемо теорему Остроградського-Гауса для випадку неперервного розподілу електричного заряду.

(3.31)

або

(3.32)

В даному випадку і 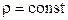, тому

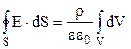. (3.33)

Виходячи з міркувань симетрії випливає, що величина Е за модулем постійна у всіх точках сферичної поверхні S, тому винесемо Е за знак інтегралу:

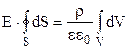. (3.34)

У формулі (3.34) інтеграл по замкненій поверхні рівний площі сферичної поверхні радіусом r а інтеграл по об’єму V рівний об’єму цієї ж сферичної поверхні, тому

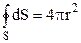, (3.35)

. (3.36)

Підставимо вирази (3.30), (3.35) і (3.36) у формулу (3.34):

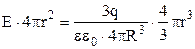
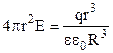
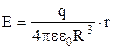. (3.37)

Отже всередині рівномірно зарядженої по об’єму кулі напруженість електричного поля прямо пропорційна відстані від центру кулі до даної точки.

Розглянемо випадок коли 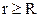, тобто визначимо напруженість електричного поля ззовні зарядженої кулі (рис. 3.6). Запишемо теорему Остроградського-Гауса.

(3.38)

або . (3.39)

Оскільки вектори 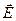і 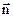мають однаковий напрямок то . Виходячи з міркувань симетрії можна стверджувати, що модуль Е однаковий в усіх точках поверхні S. Врахуємо також, що поверхня S охоплює кулю з зарядом q, тоді вираз (3.39) набере вигляду:

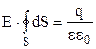. (3.40)

Підставимо (3.35) в (3.40):

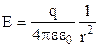. (3.41)

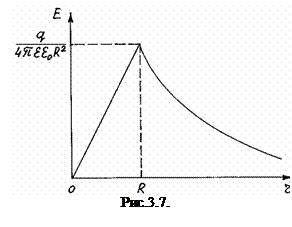Із формули (3.41) випливає, що ззовні зарядженої кулі напруженість електричного поля, так само як і для точкового заряду, обернено пропорційна квадратові відстані від центру кулі до даної точки простору.

На рис. 3.7 зображено залежність напруженості електричного поля Е від відстані r .

б) Електричне поле нескінченої рівномірно зарядженої прямої.

Розглянемо нескінченно довгу пряму, рівномірно заряджену електричним зарядом з лінійною густиною заряду .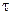

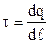. (3.42)

Лінійною густиною електричного заряду називається фізична величина рівна електричному зарядові одиниці довжини лінії вздовж якої він розподілений. У випадку рівномірного розподілу електричного заряду

, (3.43)

де 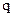– електричний заряд який розподілений вздовж лінії довжиною .

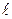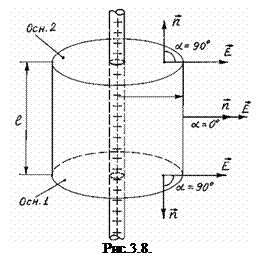
В якості замкненої поверхні виберемо циліндричну поверхню радіусом r, висотою 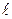, вісь якої співпадає із зарядженою прямою, як зображено на рис. 3.8. Застосуємо теорему Остроградського-Гауса:

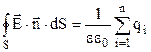. (3.44)

Інтеграл по замкненій поверхні S запишемо як суму трьох інтегралів: по бічній поверхні, по першій і другій основах. Сумарний заряд, який охоплений поверхнею S, рівний зарядові на ділянці прямої довжиною 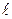. Із формули (3.43) цей заряд рівний:

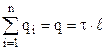. (3.45)

Підставимо (3.45) в (3.44):

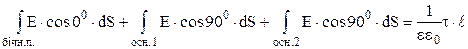
Оскільки і 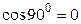, то одержимо:

.

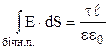З міркувань симетрії випливає, що модуль Е є однаковим в усіх точках бічної поверхні. Тому винесемо Е за знак інтегралу:

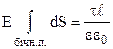. (3.46)

Інтеграл по бічній поверхні рівний площі цієї поверхні:

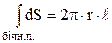. (3.47)

Підставимо (3.47) у (3.46):

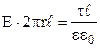
. (3.48)

З цієї формули випливає, що напруженість електричного поля, створеного нескінченою рівномірно зарядженою прямою обернено пропорційна до відстані між даною точкою простору і прямою. Ця формула справедлива також для нескінченого прямого рівномірно зарядженого циліндра.

в) Електричне поле нескінченної рівномірно зарядженої площини.

Розглянемо нескінченну площину рівномірно заряджену електричним зарядом з поверхневою густиною заряду: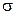

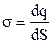. (3.49)

Поверхневою густиною електричного заряду називається фізична величина рівна електричному зарядові одиниці площі поверхні по якій розподілений заряд. У випадку рівномірного розподілу електричного заряду q по поверхні S поверхнева густина заряду рівна:

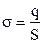. (3.50)

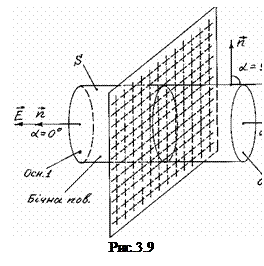В якості замкненої поверхні виберемо циліндричну поверхню з площею основи 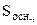вісь якої перпендикулярна до зарядженої площини, як зображено на рис.3.9.

Застосуємо теорему Остроградського-Гауса

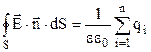. (3.51)

Інтеграл по замкненій поверхні S запишемо як суму трьох інтегралів. Сумарний заряд, який охоплений поверхнею S рівний зарядові круга площею S_осн., який вирізує циліндр S на зарядженій площині. Виходячи із формули (3.50), цей заряд рівний

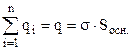(3.52)

Підставимо (3.52) в (3.51):

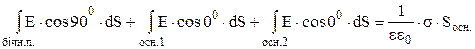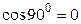Оскільки і , то

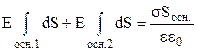. (3.53)

Інтеграли по поверхнях основ рівні:

(3.54)

Підставимо (3.54) в (3.53):

. (3.55)

Із формули (3.55) випливає, що напруженість електричного поля, створеного нескінченною рівномірно зарядженою площиною не залежить від відстані до площини, тобто є однаковою в усіх точках простору по обидва боки від зарядженої площини. Це електричне поле є однорідним. Його силові лінії перпендикулярні до зарядженої площини.

Читайте також:

1. Автоматичний розрахунок суми проведення.
2. Аеродинамічний розрахунок
3. Аеродинамічний розрахунок ротора вітроустановки
4. Аксіоми. Теореми. Ознаки.
5. Аналіз економічноїї політики за допомогою моделі Мандела-Флемінга. Випадки вільного та фіксованого валютного курсів.
6. Аналіз цін конкурентів проводиться за допомогою
7. Аналітичний розрахунок завантаження горловин
8. Аналітичний розрахунок сумарного завантаження типових перетинань
9. Булеві теореми та закони
10. Вертикальне наведення.Вертикальне наведення виконується за допомогою прицілу, бічного рівня і підйомного механізму.
11. Вибір кращих альтернатив за допомогою бінарних відношень
12. Види діелектричних втрат

Переглядів: 3290