• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Потік вектора напруженості та індукції електричного поля. Теорема Остроградського-Гауса

Нехай в просторі існує електричне поле, створене деякими електричними зарядами. Розглянемо деяку поверхню з нескінченно малою площею dS (елементарну поверхню) з одиничним вектором нормалі до поверхні 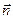, як зображено на рис.3.3. Нехай в центрі елементарної поверхні напруженість електричного поля рівна .

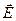Елементарним потоком вектора напруженості електричного поля називається скалярна величина, рівна скалярному добуткові вектора напруженості електричного поля і одиничного вектора нормалі на площу елементарної поверхні:

, (3.10)

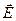де – кут між векторами і .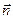

Подібним чином можна дати визначення елементарного потоку вектора індукції електричного поля, який рівний:

. (3.11)

Потік вектора напруженості електричного поля через деяку поверхню S визначається за формулою:

. (3.12)

Він пропорційний числу силових ліній, які пронизують цю поверхню.

Потік вектора індукції електричного поля через деяку поверхню S рівний:

. (3.13)

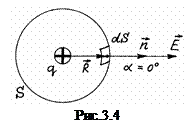
Розглянемо деякий точковий позитивний заряд , який помістимо в центрі сферичної поверхні S радіусом R (рис. 3.4). Обчислимо потік вектора напруженості електричного поля через цю замкнену поверхню

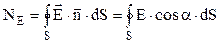. (3.14)

Напруженість електричного поля точкового заряду в будь якій точці сферичної поверхні рівна

. (3.15)

Підставимо (3.15) в (3.14), врахуємо, що кут між векторами 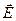і 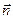в даному випадку .

.

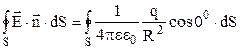Оскільки для всіх точок сферичної поверхні величина R є постійною то, винісши постійні множники за знак інтегралу, отримаємо:

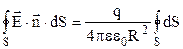. (3.16)

Але інтеграл по замкнутій поверхні S - це площа сферичної поверхні, яка рівна:

. (3.17)

Підставимо вираз (3.17) в (3.16):

. (3.18)

Український вчений М.В.Остроградський і німецький вчений К.Гаус довели, що формула (3.18) справедлива для замкненої поверхні довільної форми і довільної кількості електричних зарядів, які знаходяться всередині цієї поверхні. Тому в загальному випадку формулу (3.18) можна представити у вигляді:

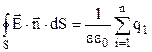. (3.19)

Формула (3.19) - це теорема Остроградського-Гауса для напруженості електричного поля:потік вектора напруженості електричного поля через довільну замкнену поверхню рівний алгебраїчній сумі електричних зарядів, охоплених цією поверхнею, поділеній на діелектричну проникність середовища.

Помножимо рівняння (3.19) на 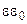. Враховуючи, що цей множник постійний, внесемо його під знак інтегралу:

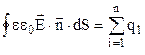. (3.20)

Враховуючи (3.7), отримаємо

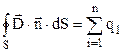. (3.21)

Формула (3.21) це теорема Остроградського-Гауса для індукції електричного поля: потік вектора індукції електричного поля через довільну замкнену поверхню рівний алгебраїчній сумі електричних зарядів, охоплених цією поверхнею.

Розглянемо випадок коли електричні заряди розподілені в просторі неперервно з деякою об’ємною густиною 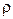. Об’ємною густиною електричного зарядуназивається фізична величина, рівна електричному зарядові в одиниці об’єму простору:

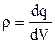. (3.22)

Визначимо з цієї формули dq:

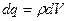. (3.23)

Проінтегрувавши вираз (3.23) по деякому об’єму V визначимо сумарний електричний заряд який міститься в цьому об’ємі:

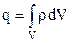. (3.24)

З врахуванням формули (3.24) теорему Остроградського-Гауса (3.19) і (3.21) у випадку неперервного просторового розподілу зарядів можна представити у вигляді:

. (3.25)

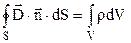. (3.26)

У формулах (3.25) і (3.26) інтегрування здійснюється по всьому об’єму V який обмежений замкненою поверхнею S.

Читайте також:

1. Аксіома математичної індукції
2. Безпечні методи звільнення потерпілого від дії електричного струму.
3. В електронагрівачах використано одну з головних власти­востей електричного струму - здатність нагрівати провідники.
4. В. Друга теорема про розклад.
5. Вектори, лінійні операції над векторами
6. Вибір і визначення магнітної індукції в елементах двигуна.
7. Види електричних травм та дії електричного струму на людину.
8. Визначення вектора за компонентами
9. Вимірювання електричного опору компенсаційним методом
10. Вимірювання електричного опору компенсаційним методом.
11. Вимірювання електричного опору методом амперметра-вольтметра
12. Вимірювання електричного опору методом омметра.

Переглядів: 3877