• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Розрахунок потенціалу електричного поля деяких заряджених тіл

Знайдемо потенціали електричних полів деяких заряджених тіл.

а). Потенціал поля рівномірно зарядженої кулі.

Розглянемо кулю радіусом 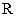, рівномірно заряджену по об’єму з об’ємною густиною 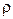і загальним зарядом ( рис.3.13 ).

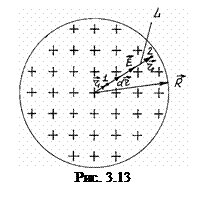Знайдемо різницю потенціалів між двома точками простору 1 і 2 на відстан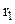і і 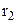від центру кулі в середині кулі . Використаємо формулу різниці потенціалів (3.73)

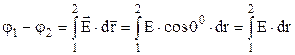. (3.86)

Підставимо вираз (3.37) напруженості електричного поля всередині зарядженої кулі у формулу (3.86)

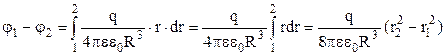
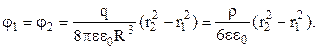(3.87)

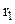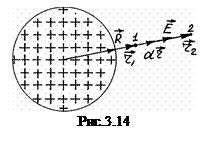
Знайдемо різницю потенціалів між двома точками простору 1 і 2 на відстані і 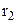від центру кулі ззовні кул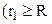і і 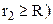, як зображено на рис. 3.14.

Підставимо вираз (3.41) напруженості електричного поля ззовні від зарядженої кулі у формулу (3.86)

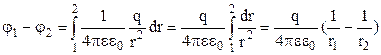. (3.88)

Формула (3.88) справедлива також і для точкового електричного заряду .

б). Потенціал поля нескінченної рівномірно зарядженої прямої

Розглянемо нескінченно довгу пряму рівномірно заряджену електричним зарядом з лінійною густиною заряду 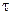. Знайдемо різницю потенціалів між двома точками простору 1 і 2 на відстан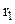і і 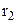від прямої

( рис. 3.15 ). Підставимо вираз (3.48) напруженості електричного поля зарядженої прямої у формулу (3.86)

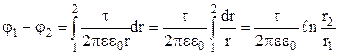. (3.89)

в). Потенціал поля нескінченої рівномірно зарядженої площини

Розглянемо нескінчену площину рівномірно заряджену електричним зарядом з поверхневою густиною заряду 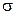. Знайдемо різницю потенціалів між двома точками простору 1 і 2 на відстані і від площини, як зображено на рис. 3.16. Підставимо вираз (3.55) напруженості електричного поля нескінченої рівномірно зарядженої площини у формулу (3.86)

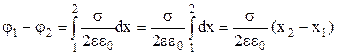
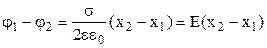. (3.90)

г). Потенціал поля електричного диполя.

Електричним диполем називається система двох однакових за модулем різнойменних зарядів. Плечемдиполя називається вектор 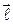напрямлений від негативного заряду до позитивного. Дипольним моментом називається векторна фізична величина, рівна добутку позитивного заряду на плече диполя

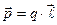. (3.91)

Знайдемо потенціал електричного поля в точці А як суму потенціалів двох точкових зарядів, які визначимо за формулою (3.69)

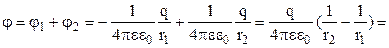
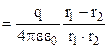. (3.92)

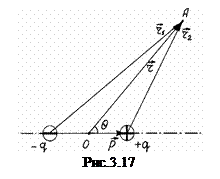Розглянемо випадок, коли точка А знаходиться на великій відстані від центра диполя порівняно із модулем плеча диполя ( рис. 3.17 ). В цьому випадку можна вважати, що 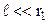; ; 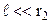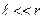, тоді можна використати наближені формули

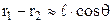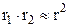, . (3.93)

Підставимо (3.93) в формулу (3.92)

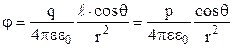. (3.94)

Читайте також:

1. Аверсивную терапію використовують, як правило, при лікуванні алкоголізму, нікотиновій залежності і деяких інших захворювань.
2. Автоматичний розрахунок суми проведення.
3. Аеродинамічний розрахунок
4. Аеродинамічний розрахунок ротора вітроустановки
5. Алгоритм формування потенціалу Ф2
6. Аналіз трудового потенціалу
7. Аналітичний розрахунок завантаження горловин
8. Аналітичний розрахунок сумарного завантаження типових перетинань
9. Базовий синтаксис деяких основних операторів
10. Безпечні методи звільнення потерпілого від дії електричного струму.
11. В електронагрівачах використано одну з головних власти­востей електричного струму - здатність нагрівати провідники.
12. Види електричних травм та дії електричного струму на людину.

Переглядів: 2365