• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Приклад 2.1

Як приклад розглянемо часову діаграму роботи багатоканальної СМО з двома пристроями (ПР1 і ПР2) і двома позиціями 1, 2 для чекання в черзі (рис. 2.9). Час надходження вимоги до системи і час, коли вона залишила систему, наведено поряд із номером вимоги відповідно в нижній і верхній частинах рис. 2.9. Час спостереження за СМО (T_сп) становить 55 хв.

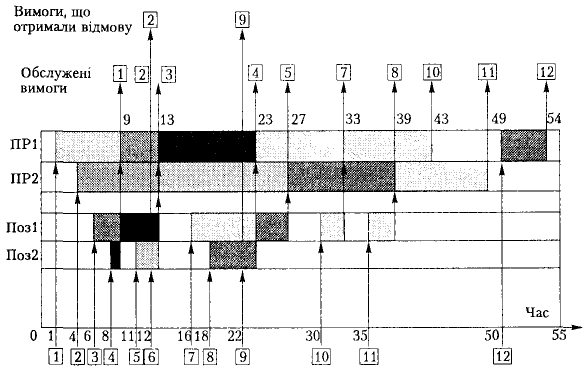
Рис. 2.9. Діаграма роботи багатоканальної СМО

На основі цієї діаграми розрахуємо значення деяких характеристик ефективності роботи СМО.

1. Імовірність обслуговування вимоги:

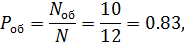
де 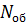і N — відповідно кількість обслужених вимог і загальна кількість вимог.

2. Пропускна здатність СМО:

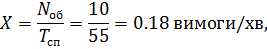
де Т_сп — час спостереження за системою.

3. Імовірність відмови в обслуговуванні:

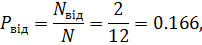
де N_від — кількість вимог, яким відмовлено в обслуговуванні.

4. Імовірність того, що вимога застане обидва пристрої вільними:

де Т_вілн — час, протягом якого обидва пристрої були вільними.

5. Імовірність того, що обслуговуванням зайнятий тільки один пристрій із двох:

де , 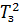— час, протягом якого були зайнятими відповідно перший і другий пристрої.

6. Імовірність того, що обслуговуванням зайняті обидва пристрої:

де 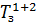— час, протягом якого обидва пристрої були зайнятими.

7. Середня кількість пристроїв, зайнятих обслуговуванням:

8. Імовірність того, що в черзі відсутні вимоги:

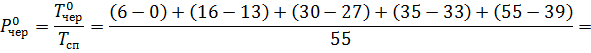
де 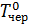— час, протягом якого в черзі не було вимог.

9. Імовірність того, що в черзі є лише одна вимога:

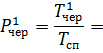
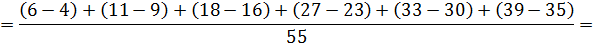
де 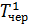— час, протягом якого в черзі перебувала лише одна вимога.

10. Імовірність того, що в черзі знаходяться дві вимоги:

де 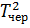— час, протягом якого в черзі було дві вимоги.

11. Середня кількість вимог у черзі:

12. Середній час перебування вимог у черзі:

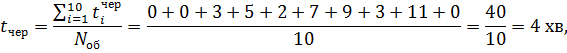
де — час перебування і-ї вимоги в черзі (і = 1, 2, ...).

13. Середній час перебування вимог у черзі без урахування вимог, які не чекали:

де 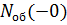— кількість вимог, які чекали в черзі.

14. Середній час обслуговування вимоги пристроями:

де 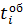— час обслуговування і-ї вимоги в СМО (і = 1, 2, ...).

15. Загальний середній час перебування вимоги в СМО:

16. Середня кількість вимог у системі обслуговування:

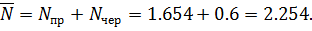
На рис. 2.10 зображено гістограму часу надходження вимог до СМО та його апроксимацію за експоненціальним законом розподілу (значення критерію Колмогорова-Смирнова для даної вибірки дорівнює 0.1345275). На гістограмі видно, що кількість вимог, які надійшли до системи, є недостатньою для статистичного оцінювання. Тому гіпотезу про експоненціальний закон розподілу надходження вимог до СМО потрібно відхилити.

Рис. 2.10. Гістограма часу надходження вимог до СМО

Отримані числові значення показників СМО мають ілюстративний характер і вказують на те, які статистичні дані необхідно фіксувати в разі моделювання СМО, щоб визначити її характеристики ефективності.

У теорії масового обслуговування розглядаються багатоканальні СМО типу M/M/m з m пристроями для обслуговування двох типів:

v з відмовами, коли зайняті всі m пристроів і вимога отримує відмову в обслуговуванні;

v з чеканням, коли зайняті всі m пристроів і вимога чекає в черзі (кількість місць чекання s), якщо в системі знаходиться m + s вимог і надходить нова вимога, то вона отримує відмову.

Для кожного з цих двох випадків можна побудувати системи диференціальних рівнянь, які описують усі стани СМО, а потім розв'язати ці рівняння за умови, що система функціонує в стаціонарному режимі. Наведемо основні формули, потрібні для розрахунків параметрів СМО типу M/M/m [41].

1. Імовірність того, що всі пристрої для обслуговування вільні:

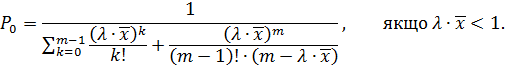
2. Імовірність того, що зайнято обслуговуванням k пристроїв або в системі знаходиться k вимог:

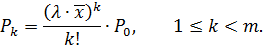
3. Імовірність того, що всі пристрої зайняті (k ³ m). Позначимо цю ймовірність через p:

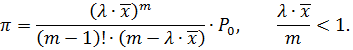
4. Імовірність того, що всі пристрої зайняті обслуговуванням і s вимог знаходяться в черзі:

5. Імовірність того, що час перебування вимог у черзі перевищує деяку задану величину t:

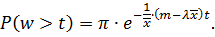
6. Середня довжина черги:

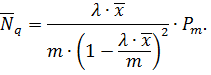
7. Середня кількість вільних від обслуговування пристроїв:

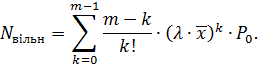
8. Середня кількість зайнятих обслуговуванням пристроїв:

9. Середній час чекання вимогою початку обслуговування в системі:

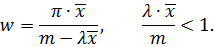
Використовуючи вищенаведені формули, можна розрахувати параметри СМО типу М/М/m, а потім порівняти їх з результатами імітаційного моделювання.

Читайте також:

1. Абсолютні синоніми (наприклад, власне мовні й запозичені) в одному тексті ділового стилю вживати не рекомендується.
2. Алгоритм однофакторного дисперсійного аналізу за Фішером. Приклад
3. Базові та прикладні класифікації
4. В чому полягає явище тунелювання через потенціальний бар’єр, наведіть приклади.
5. Визначення і приклади
6. Врахування витраті втрат електроенергії. Приклад складання електробалансу.
7. Головною метою наукової діяльності в системі вищої освіти повинен стати розвиток фундаментальних та приклад­них досліджень.
8. Деякі приклади застосування ППП
9. Дієслова з префіксом дис-виражають значення ліквідації дії, названої безпрефіксним дієсловом, наприклад: гармонізувати – дисгармонізувати, асоціювати – дисасоціювати.
10. Для одиничного і дрібносерійного виробництва норма витрати визначається як укрупнена, наприклад, на 1000 станко-годин роботи даного виду роботи устаткування
11. Додаток И - Приклад виконання ремонтного креслення деталі
12. Етикет – (прикріплювати) установлений порядок поведінки в товаристві, певному оточенні, наприклад, придворний етикет, дипломатичний етикет.

Переглядів: 1274