Аналіз вузьких місць у мережі

Пошук вузьких місць у мережі є важливим аспектом аналізу її роботи. Вузьке місце утворюється тим вузлом мережі, коефіцієнт завантаження якого наближається до одиниці. У цьому вузлі створюється велика черга вимог, яка за умови U ³ 1 стає нескінченною, тому мережа переходить у нестійкий режим роботи. Такий вузол стає «насиченим» вимогами. За впливом вузьких місць у мережі визначають її пропускну здатність. Тому під час аналізу роботи мережі потрібно особливу увагу приділяти пошуку таких місць.

Покажемо на простому прикладі, як вузьке місце впливає на пропускну здатність мережі. Розглянемо трубопровід, в якому є труби різного діаметра, що доставляють воду споживачу. Зрозуміло, що споживач не отримає води більше, ніж її може пропустити вузька труба. Це так званий ефект вузької шийки. Тому під час аналізу таких систем велике значення має балансування потоків у мережі, тобто знаходження такого балансу потоків у вузлах, при якому середній час перебування в мережі є мінімальним або її пропускна здатність максимальна.

Наведемо співвідношення, яке пов'язує коефіцієнти використання вузлів з коефіцієнтами відвідування цих вузлів:

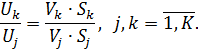
Якщо пристрій k буде «насиченим» вимогами, тобто його коефіцієнт використання становитиме приблизно 1, то під час виконання гіпотези про баланс потоків інтенсивності вихідного потоку та обслуговування будуть практично збігатись, тобто

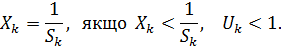
У разі збільшення кількості вимог, які одночасно обслуговуються в мережі, першим досягне насичення той вузол d, що буде мати максимальне значення величини 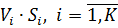тобто

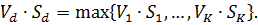
У випадку збільшення кількості вимог значення коефіцієнта використання U_d дорівнює приблизно 1 і . Оскільки 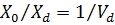, то

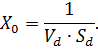
Таким чином, у разі великої кількості вимог N вихідний потік вимог від мережі повністю визначається вузлом d, що є вузьким місцем.

Визначимо мінімальний середній час перебування вимоги R₀, якщо в мережі є лише одна вимога, через коефіцієнти відвідування окремих вузлів і час обслуговування у вузлі:

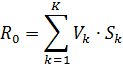
На рис. 2.21 зображено графік залежності продуктивності мережі від кількості вимог. У разі збільшення N інтенсивність X₀ монотонно зростає до граничної асимптоти , тобто доти, доки на цю інтенсивність не почне впливати потенційне вузьке місце вузла d. На рис. 2.21 через N^* позначено кількість вимог, за якої вузьке місце ще не впливає на пропускну здатність мережі.

Для замкненої мережі з кількістю пристроїв М = 1 час перебування вимоги в мережі 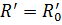R. У разі збільшення М потік вимог від мережі зростатиме, але не перевищуватиме . Таким чином,

Обчислимо значення 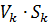для кожного з вузлів мережі:

Таким чином, мінімальний середній час перебування однієї вимоги в мережі R₀ = 1 + 0.88 + 0.32 = 2.2 с. Оскільки , то потенційним вузьким місцем у мережі є перший вузол.

За допомогою методу операційного аналізу можна знайти відповідь, наприклад, на такі запитання.

1. Яка середня кількість пристроїв М для обслуговування взаємодіє з мережею протягом усього часу спостереження? Нехай за допомогою вимірювань визначено, що Х₀ = 0.715 вимоги/с, а середній час перебування вимоги в мережі становить R = 5,2 с.

Згідно з формулою (2.19) маємо

2. Чи можна забезпечити середній час перебування вимог у мережі, який дорівнюватиме 8 с, якщо кількість пристроїв для обслуговування становить 30? Чому повинен дорівнювати максимальний середній час обслуговування вимоги в першому вузлі, щоб це стало можливим?

Згідно з формулою (2.19) маємо:

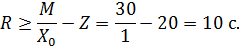
Таким чином, у разі взаємодії з мережею 30 пристроїв для обслуговування середній час перебування вимоги в ній становитиме понад 10 с.

Позначимо через допустимий середній час обслуговування вимоги. Тоді можна записати

тобто максимально можливий середній час обслуговування вимоги у вузлі 1 становить 0,047 с.

Для цього випадку на рис. 2.24 зображено графіки для асимптоти середнього часу обслуговування вимог.

Рис. 2.24. Графіки для середнього часу обслуговування вимог

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Приклад 2.2	\|	Приклад 2.5

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.