Властивості емпіричної функції розподілу

Теорема 1. Нехай X = (Х₁,..., Х_п) — вибірка об’єму п з невідомого розподілу F з функцією розподілу F. Нехай F_n^* — емпірична функція розподілу, побудована по цій вибірці. Тоді для кожного у є R

Зауваження 2.F_n^*(y) — випадкова величина, тому що вона є функцією від випадкових величин Х₁,..., Хп. Те ж саме можна сказати про гістограму і вибіркові моменти.

Доведення теореми 1.По визначенню,

Випадкові величини I(Х₁ < у), I(X₂ < у),... незалежні й однаково розподілені, їхнє математичне очікування скіннченно:

тому застосуємо ЗБЧ Хінчіна (а що це таке?), і

Таким чином, з ростом обсягу вибірки емпірична функція розподілу сходиться (по ймовірності) до невідомої теоретичної.

Насправді, вірний більш загальний результат, що показує, що збіжність емпіричної функції розподілу до теоретичного має «рівномірний» характер.

Теорема 2 (Гливенко, Кантеллі).Нехай X = (Х₁,..., Х_п) — вибірка обсягу п з невідомого розподілу У с функцією розподілу F. Нехай F_n^* — емпірична функція розподілу, побудована по цій вибірці. Тоді

Якщо функція розподілу F безупинна, то швидкість збіжності до нуля в теоремі Гливенко- Кантеллі має порядок 1/n, як показує

Теорема З (Колмогоров).Нехай X = (Х₁,...,Х_п) — вибірка обсягу п з невідомого розподілу У з неперервною функцією розподілу F. Нехай F_n^* — емпірична функція розподілу. Тоді

де випадкова величина З має розподіл Колмогорова з функцією розподілу

Випишемо ще ряд властивостей емпіричної функції розподілу, що нам будуть потрібні надалі. Це добре знайомі властивості середнього арифметичного п незалежних доданків, що мають до того ж розподіл Бернуллі.

Властивість 1. Для кожного yÎ R

, тобто величина F_n^*(y) — «незміщена» оцінка для F(y);

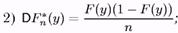
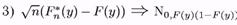
І, тобто величина F_n^*(y) «асимптотично нормальна»;

має біноміальний розподіл B_n,F(y).

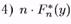
У перших трьох пунктах стверджується, що випадкова величина F_n^*(y) має математичне очікування

F(y), має убутну зі швидкістю 1/n дисперсію

Гливенко-Кантеллі, сходиться до F(y) зі швидкістю 1/n.

і, на додаток до теореми

Зауваження 3.Корисно порівняти (3) з теоремою Колмогорова.

Зауваження 4.Усі визначення, як те: «оцінка», «незміщеність», «заможність», «асимптотична нормальність» будуть дані в главі 2. Але зміст цих термінів повинний бути цілком зрозумілий уже зараз.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Збіжність емпіричних характеристик до теоретичних	\|	Доказ властивості 1.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.003 сек.