• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Доказ властивості 1.

1) Випадкові величини I(Х₁ < у), I(Х₂ < у),... однаково розподілені, тому (де використовується однакова распреділеність?)

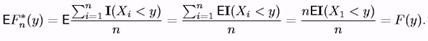
2)Випадкові величини I(Х₁ < у), 1(Х₂ < у),... незалежні й однаково розподілені, тому (де використовується незалежність?)

Ho di(x <y) = F(y)(1 - F(y)), оскільки І(Х < у) B_F(y).

3) Скористаємося ЦПТ Ляпунова (а що це таке?).

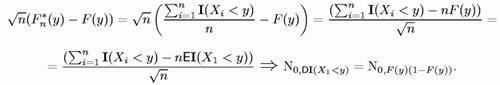
4) Оскільки I(Х₁ < у) (число успіхів в одному іспиті) має розподіл Бернуллі В_F(y) (ще
раз - чому?), те п • F_n^*(y) = åⁿ_i=1 I(X₁ < y) біноміальний розподіл В_n,F(y)(чому?
і при чому тут зміст біноміального розподілу? а також при чому тут його стійкість по сумуванню?).

Властивості гістограми Нехай ¦ — щира невідома щільність розподілу В (якщо В абсолютно безупинно). Нехай, крім того, число k інтервалів групи не залежить від п. Див. зауваження 5 для випадку, коли k = k(n). Справедлива

Теорема 4. При п ® µдля будь-якого j = 1,..., k

Якщо, до того ж, щира щільність f(x) безупинна на інтервалі a_j , то інтеграл праворуч дорівнює lj • f(uj), де uj -деяка крапка усередині інтервалу угруповання a_j (знайдеться по теоремі про середній).

Вправа. Довести теорему 4, використовуючи (1) і ЗБЧ.

Теорема затверджує, що (для безупинної щільності) висота стовпця гістограмми, побудованого над інтервалом угруповання, з ростом обсягу вибірки зближається зі значенням щільності розподілу в одній із крапок цього інтервалу. Або (для довільної щільності) площа відповідного стовпця гістограмми зближається з площею над тим же інтервалом під графіком щільності.

Вправа. Намалювати твердження теореми 4 на графіку щільності / гістограмми.

Зауваження 5. Помітимо, що чим більше інтервалів угруповання, тим краще. Але це «чим більше» має свої границі: якщо брати число інтервалів, скажемо, порядку п, те з ростом п гістограмма не буде поточечно сходитися до щільності.

Справедливо наступне твердження: якщо щільність розподілу елементів вибірки є безупинною функцією і k(n)/n ® 0, то має місце поточечна збіжність гістограмми до щільності (див. зауваження 1).

Зі своєї сторони, можу запропонувати завжди брати число інтервалів, скажемо, рівне цілої частини від кореня п'ятого ступеня з п (помноженого на е^p, якщо обсяг вибірки більше 413):

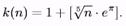
Читайте також:

1. Аеродинамічні властивості колісної машини
2. Аналізатори людини та їхні властивості.
3. Аналізатори людини та їхні властивості.
4. Атрибутивні ознаки і властивості культури
5. Аудиторські докази щодо тверджень керівництва у фінансових звітах отримуються безпосередньо в процесі проведення тестів контролю та процедур по суті.
6. Аудиторські докази.
7. Аудиторські докази: поняття та процедури отримання
8. Білки, властивості, роль в життєдіяльності організмів.
9. Біосфера Землі, її характерні властивості
10. Будова атомів та хімічний зв’язок між атомами визначають будову сполук, а отже і їх фізичні та хімічні властивості.
11. Будова і властивості аналізаторів
12. Валідація НАССР- отримання об'єктивного доказу того, що елементи НАССР-плану результативні.

Переглядів: 717