• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Методи знаходження оцінок: метод моментів

Метод моментів полягає в наступному: будь-який момент випадкової величини Х_k (наприклад, k-й) є функція від параметра q. У свою чергу, параметр q є функція (зворотна, якщо існує) від теоретичного k-ro моменту. Підставивши в цю функцію замість невідомого теоретичного k-ro моменту його вибірковий аналог, дістанемо замість параметра q оцінку q*.

Отже, нехай X1,..., Хп вибірка об'єму п з параметричного сімейства розподілів ¦_q, де q Î Q. Нехай

причому функція h оборотна. Тоді як оцінка в* для в беремо рішення рівняння

Або (що те ж саме), спочатку вирішується рівняння (3) відносне q, а потім замість істинного моменту беремо вибірковий:

Можна сказати, що ми беремо як оцінка таке (випадкове) значення параметра q, при якому істинний момент співпадає з вибірковим.

Приклад 4Нехай Х₁,...,Х_п — вибірка об'єм п, весь X_i Î U_0,q, де q > 0. Знайдемо оцінку метода момента (ОММ) по перший моменту:

Знайдем оцінку метода моментів (ОММ) по k-му моменту:

Перевірим властивість отриманих оцінок. Незміщеність:

2. Розглянути оцінка q_оцінкаЗаметим, що Е_qq₂^* = Е_що, тогда як q = 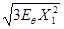= (по лемеі 1).

Рівність Е_qq₂^* = 0 означати би, що для с.в. x = 3Х² виконувати Е_q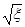= 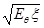, а для величина h = 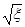виконувати Е_qh² = (E_qh)².

Пригадати той єдиний випадок, коли це можливо, щоб погодитися з висновком: оцінка q₂^* = — зміщати (як, проте, и оцінка q_k^*, k > 2).

Спроможність:

1. По ЗБЧ, q₂^* = 2Х 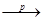2E_qX₁ = 2q/2 = q Þ q₁^* = 2Х — спроможний.

2. Помітити, що по ЗБЧ (або по лемме 3 — тільки для тех, хто ее доводити) при п ®¥

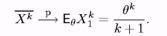
3. Оскільки функція безперервний для весь у > 0, то при п ®¥

Вправа.Навіщо потрібен посилання на безперервність функція ?

Тобто вся послідовність

складається з спроможних оцінок, при цьому

тільки оцінка q₁* = 2Х — незміщена.

Зауваження7 Може траплятися так, що оцінка q* Ï Q_, тоді як q Î Q. В цей випадок в якість оцінка берет найближчий к q* точка из Q, на худий кінець — з замикання Q, якщо Q не замкнутий.

Приклад 5прикладПусть X₁,..., Х_п — вибірка об'єм п, весь X_i ÎN_a,1, де по який-то причина а ³_ 0. Шукати оцінка для а по перший момент:

Однак по умові а ³ 0, тоді як X може бути і негативний. Зрозумілий, що якщо X < 0, то в якість оцінка для позитивного парметру а більше підійти 0. Якщо же X > 0, в якість оцінка треба брати X. Разом: а* = max{0, X} — оцінка метод момент.

Читайте також:

1. D) методу мозкового штурму.
2. H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
3. I Метод Шеннона-Фано
4. I. Метод рiвних вiдрiзкiв.
5. VII. Нахождение общего решения методом характеристик
6. А. науковий факт, b. гіпотеза, с. метод
7. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
8. Агрегативна стійкість, коагуляція суспензій. Методи отримання.
9. АгротехнІЧНИЙ метод
10. Адаптовані й специфічні методи дослідження у журналістикознавстві
11. Адміністративні (прямі) методи регулювання.
12. Адміністративні методи - це сукупність прийомів, впливів, заснованих на використанні об'єктивних організаційних відносин між людьми та загальноорганізаційних принципів управління.

Переглядів: 1594