• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Методи знаходження оцінок: метод максимальної правдоподібності

Доказ теореми 5.

Спроможність оцінок методу моментів

Теорема 5.Нехай q* = h^-1(Xk) оцінка параметра в, отримана по методу моментів, причому функція h^-1 безперервна. Тоді q* спроможна.

По лемме 3 маємо: X^k 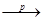E_qX₁^k = h(q). Оскільки функція h^-1 безперервна, то і

Зауваження8. Для оборотної, тобто взаімнооднозначной функції h: R ® Rбезперервність h і безперервність h^-1еквівалентні.

Метод максимальної правдоподібності ще один розумний спосіб побудови оцінки невідомого параметра. Складається він в тому, що як «найбільш правдоподібне» значення параметра беруть значення в, максимизирующее імовірність отримати при n дослідах дану вибірку X = (Х₁,..., Хп). Це значення параметра залежить від вибірки і є шуканою оцінкою.

Вирішимо спочатку, що таке «імовірність отримати дану вибірку», тобто що саме треба максималізувати. Пригадаємо, що для абсолютно безперервних розподілів Á_q їх щільність f_q(у) «майже» (з точністю до dy) імовірність попадання в точку у. А для дискретних розподілів Á_q імовірність попасти в точку у рівна P_q(X₁ = у). І те, і інше ми будемо називати щільністю розподілу Á_q (відступаючи при цьому, для простоти, від термінології теорії імовірностей). Отже,

Визначення 5.Функцію

ми будемо називати щільністю розподілу F.

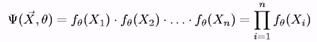
Визначення 6.Функція (взагалі кажучи, випадкова величина)

називається функцією правдоподібності. Функція (також випадкова)

називається логарифмічною функцією правдоподібності.

Якщо наша вибірка X в даній серії експериментів прийняла значення (x₁,..., х_n), те (в дискретному випадку) функція правдоподібності і є імовірність цієї події, різна при різних значеннях параметра в:

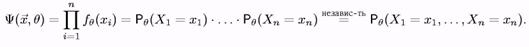
Визначення7. Оцінкою максимальної правдоподібності q невідомого параметра qназивають значення q, при якому функція Y(Х, q) досягає максимума (як функція від в при фіксованих X₁,..., Х_n):

q = точка максимума (по змінній q) функції Y(Х, q)

Зауваження 9.Оскільки функція ln у монотонна, то точки максимума Y(X, q) і L(X, q) співпадають. Тому оцінкою максимальної правдоподібності (ОМП) можна називати точку максимума (по в) функції L(х, q):

q = точка максимума (по змінній q) функції L(X, q).

Нагадаємо, що точки экстремума функції це або точки, в яких похідна звертається в нуль, або точки розриву функції/похідного, або крайні точки області визначення функції.

Приклад 6.Нехай Х₁,..., Хп вибірка об'єму п з розподілу Пуассона: X_i Î П_l, де l > 0. Найдем ОМП А невідомого параметра l.

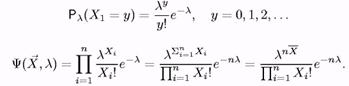
Оскільки ця функція при всіх l > 0 безперервно диференціюється по l, можна шукати точки экстремума, прирівнявши до нуля приватну похідну по l. Але зручніше це робити для логарифмічної функції правдоподібності:

і точка экстремума l рішення рівняння: 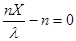, тобто l =X.

Читайте також:

1. D) методу мозкового штурму.
2. H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
3. I Метод Шеннона-Фано
4. I. Метод рiвних вiдрiзкiв.
5. VII. Нахождение общего решения методом характеристик
6. А. науковий факт, b. гіпотеза, с. метод
7. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
8. Агрегативна стійкість, коагуляція суспензій. Методи отримання.
9. АгротехнІЧНИЙ метод
10. Адаптовані й специфічні методи дослідження у журналістикознавстві
11. Адміністративні (прямі) методи регулювання.
12. Адміністративні методи - це сукупність прийомів, впливів, заснованих на використанні об'єктивних організаційних відносин між людьми та загальноорганізаційних принципів управління.

Переглядів: 804