Крапкові оцінки. Незміщенність, спроможність оцінок

Отже, нехай Х,..., Хп вибірка об'єму п з параметричного сімейства розподілів . Помітимо, що всі характеристики випадкових величин Х,..., Хп залежать від параметра θ. Так, наприклад, для Хі Є П_λ:

Щоб відобразити цю залежність, будемо писати Е_θХ₁ замість ЕХ₁ і т.д. Так, D_θ1Х₁означає дисперсію, обчислену в припущенні θ = θ₁.

Вправа.Нехай Х₁ Є Bp, p₁= 0,5, р₂ = 0,1. Обчислити Е_РІХ₁, Е_Р2Х₁.

Визначення 2.Статистикою називається будь-яка (вимірна!) функція θ* = θ*(Х₁,..., Хп).

Зауваження 6.Статистика є функція від емпіричних даних, тобто від вибірки Х₁,..., Хп, але ніяк не від параметра в. Статістіка, як правило, предназначена саме для оцінювання невідомого параметра в (у цьому разі її називають «оцінкою»), і вже тому від нього залежати не повинна.

Взагалі кажучи, статистика є не «будь-хто», а «вимірна» функція від вибірки, але оскільки на практиці іншого не буває: ), ми на це звертати увагу не будемо.

Визначення 3.Статистика q* = q*(X₁,... ,Х_п)) називається незміщеною оцінкою параметра в, якщо для будь-кого q Î Q

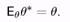
Незміщеність властивість оцінок при фіксованому п. Означаєт ця властивість відсутність помилки «в середньому», тобто при систематичному використанні даної оцінки.

Визначення 4.Статистика q* = q*(Х₁,... ,Х_п)) називається спроможною оцінкою параметра в, якщо для будь-кого q Î Q

Властивість спроможності означає, що оцінка наближається до невідомого параметра при збільшенні кількості даних. Зрозуміло, що при відсутності цієї властивості оцінка абсолютно «неспроможна» як оцінка.

Приклад 3.Нехай Х1,..., Хп вибірка об'єму п, все X_i Î N_a_,_s₂, де R, s > 0. Как знайти оцінки для параметрів а і s², якщо обидва ці параметри (можна вважати це і одним двумірним параметром) невідомі?

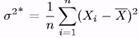
Ми вже знаємо хороші оцінки для теоретичного середнього, дисперсії будь-якого розподілу. І оскільки a = E_a_,_s²X₁^, візьмемо в якості оцінки для а вибіркове середнє: а* = X. Лема 1 стверджує, що ця оцінка незміщена і спроможна.

Оскільки

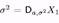
, тобто навіть дві оцінки:

незміщена вибіркова дисперсія.

- вибіркова дисперсія і

Як показано в лемі 2, обидві ці оцінки спроможні, і одна з них незміщена (яка?).

Але такі «способи» отримання оцінок потребують систематизації. Помітимо відразу, що приведені нижче методи отримання оцінок ні з яких математичних аксіом не виводяться. Вони просто розумні з практичної точки зору. Саме на їх разумність потрібно звернути увагу.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Параметричні сімейства розподілів	\|	Методи знаходження оцінок: метод моментів

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.