Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Щільність f(x, y) імовірностей системи двох неперервних випадкових величин (Х, Y), та її властивості

Характеристикою системи неперервних випадкових величин є щільність імовірностей.

Для визначення щільності ймовірностей системи двох неперервних випадкових величин (Х, Y) застосовується формула (18).

Розглянемо прямокутник зі сторонами Dх та Dу (рис. 5).

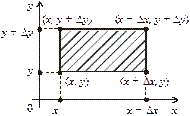
Рис. 5

Імовірність розміщення системи (Х, Y) у прямокутній області
(x < X < x + Dx, y < Y < y + Dy) обчислюється за формулою

P(x < X < x + Dx, y < Y < y + Dy) =
= F(x + Dx, y + Dy) + F(x, y) – F(x + Dx, y) – F(x, y + Dy).

Поділивши цю ймовірність на площу прямокутника Dx, Dy і спрямувавши Dx ® 0, Dy ® 0, дістанемо ймовірність у точці, тобто щільність:

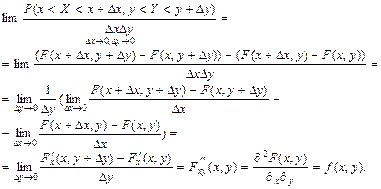
Отже,

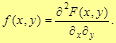(19)

Функція f (x, y) може існувати лише за умови, що F (x, y) є неперервною за аргументами х і у та двічі диференційовною.

Функції f (x, y) у тривимірному просторі відповідає певна поверхня — так звана поверхня розподілу ймовірностей системи двох неперервних випадкових величин (Х, Y).

Тоді f (x, y) dxdy — імовірність розміщення системи двох випадкових величин у прямокутнику зі сторонами dx, dy.

Властивості f (x, y)

1. Функція f (x, y) ³ 0, оскільки F(x, y) є неспадною відносно аргументів х і у.

2. Умова нормування системи двох неперервних випадкових величин (Х, Y) така:

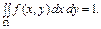(20)

Якщо , то (131) набирає такого вигляду:

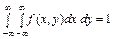. (21)

3. Імовірність розміщення системи змінних (х, у) в області 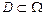обчислюється так:

(22)

Імовірність розміщення системи змінних (х, у) у прямокутній області D = (a < x < b, c < y < d)

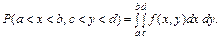(23)

4. Функція розподілу ймовірностей системи двох змінних визначається з рівняння

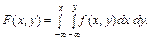(24)

5. Якщо 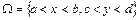, то (25)

Приклад 5. Задано

f (x, y) = a, якщо (x, y) Î W, a = const;

f (x, y) = 0, якщо (x, y) Ï W,

де W = (–2 £ x £ 4, –3 £ y £ 5).

Знайти a і F(x, y). Обчислити P(–1 < x < 2, –2 < y < 3).

Розв’язання. Множина W зображена на рис. 6.

Рис. 6

Для визначення а застосовуємо умову нормування (20):

де .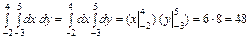

Отже, маємо

f (x, y) = 1/48, якщо (x, y) Î W,

f (x, y) = 0, якщо (x, y) Ï W.

Згідно зі (136) при –2 < x < 4, –3 < y < 5 дістанемо:

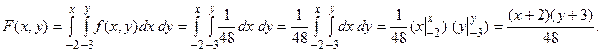
Якщо –2 < x < 4, y > 5, то

Якщо x > 4, – 3 < y < 5, то

Звідси

7. Основні числові характеристики для системи двох неперервних випадкових величин (Х, Y)

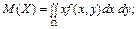
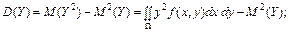
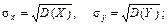
Якщо, то виконуються співвідношення:

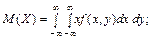
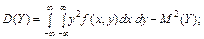
Якщо 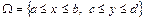, то маємо:

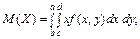
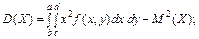
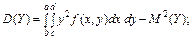
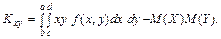
8. Умовні закони розподілу для неперервних випадкових величин Х і Y, які утворюють систему (Х, Y) (на «5» балів)

Як і в системі двох дискретних випадкових величин, у системі двох неперервних випадкових величин розглядаються умовні закони розподілу.

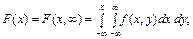
Звідси

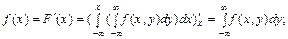
Умовні закони розподілу для неперервних випадкових величин Х, Y, що утворюють систему (Х, Y), визначаються умовними щільностями ймовірностей f (x / y), f (y / x):

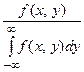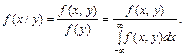
Тому дістаємо

f (x, y) = f (x) f (y / x) = f (y) f (x / y).

Для умовних законів розподілу неперервних випадкових величин умова нормування має такий вигляд:

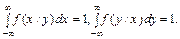
Якщо випадкові величини Х та Y є незалежними, то

f (x / y) = f (x), f (y / x) = f (y).

f (x, y) = f (x) f (y).

Для незалежних випадкових величин Х та Y виконується рівність

F(x, y) = F(x) F(y).

Числові характеристики для умовних законів розподілу ймовірностей:

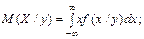
9. Стохaстична залежність (на «5» балів)

Дві випадкові події називаються незалежними, якщо

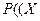
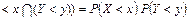, або F(x, y) = F(x) F(y).

Для неперервних випадкових величин Х і Y умовy незалежності можна подати через щільності ймовірностей:

f (x, y) = f (x) f (y).

Умову незалежності можна записати і так:

f (x / y) = f (x), f (y / x) = f (y).

Залежність випадкових величин у певному розумінні є узагальненням поняття функціональної залежності. Якщо в разі функціональної залежності між величинами Х та Y кожному значенню Х = х відповідає певне значення Y = у, то в разі залежності між випадковими величинами Y і Х кожному можливому значенню Х = х відповідає множина значень Y, які характеризуються умовними щільностями ймовірності f (y / x).

Отже, залежність між випадковими величинами означає аналітичну залежність щільності умовного розподілу однієї з них від значень, яких набуває друга величина. Таку залежність називають стохастичною або ймовірнісною. Виявляється вона не лише у зміні умовних законів розподілу, а й у зміні умовних числових характеристик: M (X / y), M (Y / x), D (X / y), D (Y / x), тобто умовних математичних сподівань та умовних дисперсій (рис. А—F).

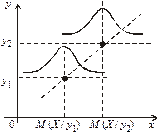
Рис. А. Стохастична і кореляційна залежність між Y та Х, М (Y / х) = a(х)

Рис. B. Стохастична і кореляційна залежність між Х та Y, М (X / у) = b(у)

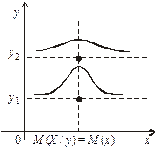
Рис. С. Стохастична залежність між Y та Х, D (Y / х) = a(х); кореляційний зв’язок відсутній

Рис. D. Стохастична залежність між Х і Y, D (X / у) = b(у); кореляційний зв’язок відсутній

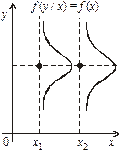
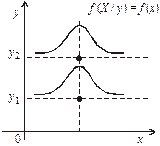
Рис. Е. Незалежні випадкові величини

Рис. F. Незалежні випадкові величини

Отже, рис. А, В ілюструють те, що кореляційною залежністю між випадковими величинами Y і Х є функціональна залежність умовних математичних сподівань М (X / у), М (Y / х) від аргументів у та х:

М (X / у) = a(у). М (Y / х) = b(х).

Ці рівняння називають рівняннями регресії. Якщо М (Y / х) = М (y), М (X / у) = М (х), то кореляційна залежність відсутня, але існує стохастична залежність (див. рис. С і D), оскільки змінюються умовні дисперсії. Випадок, коли між Х і Y відсутня стохастична, а отже, і кореляційна залежність, ілюструють рис. Е і F.

Отже, якщо між випадковими величинами Y і Х існує кореляційна залежність, то між ними обов’язково іcнує й стохастична залежність. Але за наявності стохастичної залежності між випадковими величинами Х і Y кореляційної залежності між ними може й не бути.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Доведення.	\|	Розв’язання.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.006 сек.