
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Лекція 2 Операції над подіями. Теорема додавання ймовірностей. Умовні ймовірності. Теорема множення ймовірностей. Ймовірність здійснення принаймні однієї з незалежних подій
ОзначенняПротилежними називаються події А і 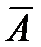 ( не А), які утворюють повну групу (рис. 2).
( не А), які утворюють повну групу (рис. 2).
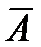
|
| А |
Рис. 1
Рисунок 2
Прикладом А і 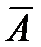 є поява аверса і реверса при киданні монети.
є поява аверса і реверса при киданні монети.
ОзначенняДобутком подій А і В називається подія А·В, яка полягає в одночасній появі А і В (рис.3).
| А·В |
| А |
| В |
Рисунок 3
ОзначенняСумою подій А і В називається подія А + В , яка полягає в появі А або В ( або АВ ) (рис.4).
| А В А + В |
Рисунок 4
Аналогічно визначаються добуток і сума більшого числа подій.
Теорема 1 Імовірність суми сумісних подій А і В дорівнює сумі ймовірностей цих подій без ймовірності їх добутку
Р ( А + В) = Р (А) + Р (В ) - Р ( А·В)
Теорема 2Якщо А і В несумісні, то А·В =V, Р (А·В) = 0 і тоді ймовірність суми несумісних подій А і В дорівнює сумі ймовірностей цих подій
Р ( А + В ) = Р (А ) + Р ( В ).
Останнє співвідношення можна використати як означення несумісних подій.
Н а с л і д о к 1. Якщо події А1, А2, . . . Аn попарно несумісні, то
Р (А1 + А2 + . . .+ Аn ) = Р (А1) + Р ( А2) + . . . + Р ( Аn)
(треття аксіома А. Колмогорова).
Н а с л і д о к 2. Сума ймовірностей попарно несумісних подій, які утворюють повну групу, дорівнює одиниці:
Р ( А1 ) + Р ( А2 ) + . . . +Р (Аn) = 1
Н а с л і д о к. 3. Сума ймовірностей взаємо протилежних подій дорівнює одиниці:
Р ( А ) + Р ( 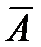 ) = 1.
) = 1.
Так, якщо ймовірність влучення в ціль Р (А) = 0,8, то ймовірність промаху q = 1 – Р ( А) = 0,2.
Події А і В можуть бути залежнимий незалежними. У першому випадку поява А впливає, а в другому не впливає на ймовірність появи В.
Приклад
У ящику чотири білих і три чорних кулі. В результаті першого випробування ( вилучення кулі з ящика) з’явилася чорна куля ( подія А). Знайти ймовірність появи білої кулі ( подія В) в другому випробуванні, якщо: а) кулю повертають в ящик, в) кулю не повертають після першого випробування.
Розв’язування. Маємо а) Р(В) = 4 / 7 – незалежна подія;
в) Р ( В/А ) = 4 / 6 = 2 / 3 – залежна подія.
ОзначенняУмовною ймовірністю Р (В/А ) називається ймовірність події В за умови, що подія А відбулась.
Теорема 3 Ймовірність добутку двох залежних подій А і В дорівнює добутку ймовірності однієї з цих подій на умовну ймовірність іншої
Р ( А·В ) = Р (А)· Р (В/А) = Р (В)· Р ( А /В ).
Н а с л і д о к. Р (В / А ) = Р ( А·В) / Р ( А ).
Теорема 4Ймовірність добутку незалежних подій А і В дорівнює добутку ймовірностей цих подій
Р ( А·В ) = Р (А )· Р ( В ).
Ця теорема випливає з попередньої. Крім того, можна довести, що коли А і В незалежні, то незалежні також А і 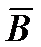 ,
,  і В,
і В,  і
і 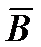 .
.
Читайте також:
- А. Це наявність в однієї людини кількох ліній клітин з різним набором хромосом.
- А/. Форми здійснення народовладдя та види виборчих систем.
- Автододавання та автообчислення.
- Аксіоми додавання і множення
- Активні операції банків
- Активні операції комерційних банків
- Алгебра випадкових подій
- Алгебра подій
- Алгебраїчні операції
- Алгоритм здійснення купівлі
- Алгоритми переведення чисел з однієї позиційної системи числення в іншу
- Алгоритмічна конструкція повторення та її різновиди: безумовні цикли, цикли з після умовою та з передумовою.
| <== попередня сторінка | | | наступна сторінка ==> |
| Домашнє завдання | | | Ймовірність появи хоча б однієї події |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |