- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Метод Жордана-Гаусса
При дослідженні економічних об’єктів виникає потреба в розв’язуванні системи лінійних алгебраїчних рівнянь з багатьма не-відомими. Більш зручним для цього є модифікований метод Жорда-
на-Гаусса. Він полягає в повному виключенні невідомих.
Дамо коротку схему цього методу.
За перше рівняння візьмемо таке рівняння, в якому коефіцієнт (його назвемо ключовим елементом) біля x1 відмінний від нуля і
розділимо на нього все рівняння. З допомогою цього рівняння ви-ключимо невідоме x1 в усіх рівняннях, крім першого. Аналогічно
невідоме x2 виключимо в усіх рівняннях, крім другого і т.д. При цьому можливі три випадки.
1. Ліва частина i -го рівняння системи перетворилась в нуль,
а права частина рівна деякому числу, відмінному від нуля. Це зна-чить, що система лінійних рівнянь немає розв’язків.
2. Ліва і права частини i -го рівняння системи перетворились
в нуль. В цьому випадку i -те рівняння можна відкинути.
3. У випадку використання всіх рівнянь, в процесі виключеня невідомих, одержуємо розв’язок даної системи.
Зауваження. Якщо в першому рівнянні вихідної системи кое-
фіцієнт біля x1 рівний нулю, то можна взяти інше рівняння, в якому
за ключовий елемент візьмемо відмінний від нуля коефіцієнт при x1 .
Приклад 1.Розв’язати методом Жордана-Гаусса систему лі-нійних рівнянь
| 2 x1 − x2 − x3 = 2, | ||
| + x2 − x3 = 0 , | ||
| 3 x1 | ||
| − 3 x2 + x3 = 1. | ||
| − 4 x1 |
Розв’язування. За ключовий елемент виберемо коефіцієнт“2”біля x1 в першому рівнянні, оскільки він відмінний від нуля. Розді-
лимо перше рівняння на це число “2”:
| − | − | 3 = 1, | |||||||
| x1 | x2 | x | |||||||
| = 0 , | |||||||||
| 3 x1 | + x2 | − x3 | |||||||
| + x3 = 1. | |||||||||
| − 4 x1 − 3 x2 | |||||||||
Виключимо невідоме x1 в другому і третьому рівняннях. Для
цього додамо до другого рівняння перше, помножене на “-3”, а до третього – перше, помножене на “4”.
Тобто перший крок є такий самий, як в методі Гаусса:
| − | x2 − | = 1, | |||||||||
| x1 | x3 | ||||||||||
| x | 2 + | x | 3 =−3, | ||||||||
| − | = 5. | ||||||||||
| 5 x2 | − x3 | ||||||||||
Серед двох рівнянь (друге і третє) виберемо за ключовий еле-мент відмінний від нуля коефіцієнт, який стоїть біля x2 ,
Наприклад, число “ 5 ”. Розділимо на це число друге рівняння:
2
| − | x2 − | = 1, | ||||||||
| x1 | x3 | |||||||||
| x2 + | x3 | = − | , | |||||||
| 5. | ||||||||||
| − 5 x2 − x3 = | ||||||||||
В цих рівняннях, крім другого, виключимо невідоме х2. Для цього додамо до першого і третього рівнянь друге, помножене на
“0,5” і “5”:
| x1 | − | x3 = | , | ||||||||||
| x2 | + | x3 =− | , | ||||||||||
| 0 = | |||||||||||||
| 1. | |||||||||||||
Це означає, що третьому рівнянню не можуть задовольняти жодні значення невідомих. Тобто вихідна система рівнянь розв’язків немає.
Особливо зручно користуватись методом Жордана-Гаусса в матричній формі, яка представлена таблицею. При цьому її перетво-рення здійснюється з допомогою певних кроків.
1. Вибираємо ключовий елемент aij ≠ 0 . Ключовий рядок на
кожному етапі вибирається інший так, щоб йому відповідала тільки одна невідома.
2. Елементи i -го рядка (ключового) ділимо на aij і записує-мо в i -ий рядок наступної розрахункової таблиці.
3. Елементи ключового стовпця (крім ключового елемента, який рівний 1 ) записуємо нульовими.
4. Інші елементи наступної розрахункової таблиці (в тому числі і контрольного стовпця) обчислюємо за формулою
| ′ | = akl − | ail | ( k = 1,2,...,n;l = 1,2,...,n;k ≠ i ; k ≠ l ) . | ||
| akl | akl | ||||
| aij | |||||
5. Порівнюємо суму елементів рядка розрахункової таблиці з відповідним елементом контрольного стовпця ( Σ ).
Перехід від однієї матриці-таблиці до іншої за методом Жор-дана-Гаусса називається симплексним перетворенням матриць-таблиць.
Приклад 2.Розв’язати методом Жордана-Гаусса систему
| 2 x1 + x2 − 4 x3 =−1, | ||||
| лінійних рівнянь: | + x3 | = 6 , | ||
| 4 x1 + 3 x2 | ||||
| + x3 | = 8. | |||
| 3 x1 − x2 |
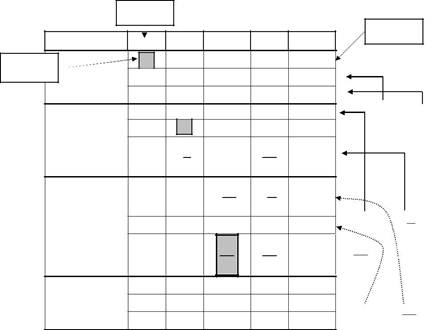
Розв’язування. Запишемо задану систему в табличній формі.За ключовий елемент тут взято коефіцієнт “2” при х1 в першому рівнянні і взято в рамки. Стовпець ∑ є контрольним, а елементи йо-го дорівнюють сумі інших чисел цього рядка, тобто сумі коефіцієн-тів біля невідомих і вільного члена відповідного рівняння.
Таблиця 1.За ключовий елемент взято число“2”.Поділившина нього елементи першого рядка, одержимо відповідні елементи
першого рядка таблиці 2(на це вказує число “ 1 ” в першому рядку
2
поза таблицею).
Таблиця 2.Напроти першого рядка записано число“-4”і на-правлена стрілка до другого рядка табл.1. Це означає, що елементи першого рядка множаться на “-4” і додаються до відповідних елементів другого рядка табл.1. Число “-3” і стрілка, направлена до третьої стрічки означає,що на це число “-3” множаться всі елементи першого рядка табл.2 і додаються до відповідних елементів третього рядка табл.1. Цим самим в табл. 2 в першому стовпці під числом “1” отримали нульові елементи. За ключовий елемент цієї таблиці ви-
бираємо число “1” в другому рядку (взято в рамку). Запис “ − 1 ” із
2
стрілкою до першого рядка означає, що елементи ключового рядка
другої таблиці потрібно помножити на “ − 1 ” і додати до
2
відповідних елементів першого рядка. Цим самим отримаємо еле-менти таблиці 3.
Аналогічно - “ 5 ” і стрілка до третього рядка означає мно-
2
ження елементів ключового рядка цієї таблиці на “ 5 ” і додавання
2
до відповідних чисел третього рядка для запису в третьому рядку таблиці 3.
Результатом виконання дій цієї таблиці є виключення невідомої x1 із другого і третього рівнянь системи.
Таблиця 3. За ключовий елемент цієї таблиці взято“ 59 ”із
2
третього рядка і третього стовпця (взято в рамку). Запис “ 2 ” в цій
59
стрічці поза таблицею означає, що всі її елементи треба помножити на це число, тобто робимо ключовий елемент одиницею. Результат множення записуємо третім рядком табл. 4. Підсумком виконання цих дій табл. 3 є виключення невідомої x2 з першого і третього
рівнянь.
Таблиця 4. Числа“-9”і“ 13 ”,які записані справа від таблиці
2
із стрілками до другого і першого рядків табл. 3 означають: елемен-
| ти третього рядка табл.4 множимо на “-9” і “ 13 ” і додаємо до від- | ||||||||
| 2 | ||||||||
| повідних елементів другого і першого рядків табл.3. | ||||||||
| Ключовий | ||||||||
| стовпець | Ключовий | |||||||
| № таблиці | x1 | x2 | x3 | bi | ∑ | рядок | ||
| Ключовий | -4 | -1 | -2 | ×(½) | ||||
| елемент | + | |||||||
| -1 | ||||||||
| + | ||||||||
| ½ | -2 | −½ | -1 | ×(-4), (-3) | ||||
| - 5 | ||||||||
| + | ||||||||
| - 13 | - 9 | + | ||||||
| -10 | ||||||||
| 2 | ×(-½) ( 5 ) | |||||||
| 59 ×( 2 ) + + | ||||||||
| -1 | ×(-9), ( 13 ) | |||||||
| Останній таблиці 4 відповідає така система рівнянь: | ||||||||
| 1 ⋅ x1 + 0 ⋅ x2 + 0 ⋅ x3 = 2, | ||||||||
| ⋅ x1 | + 1 ⋅ x2 + 0 ⋅ x3 | =−1, | ||||||
| 0 | ||||||||
| + 0 ⋅ x2 | + 1 ⋅ x3 | = 1, | ||||||
| 0 ⋅ x1 | ||||||||
| тобто | x1 = 2; x2 =−1; x3 = 1 є розв’язком вихідної системи трьох | |||||||
| лінійних рівнянь з трьома невідомими. | ||||||||
| Зауваження 1. Ключовий елемент вибирається тільки один раз | ||||||||
| у відповідному рядку або стовпці. | ||||||||
| Зауваження 2. Ключовий елемент не вибирається серед віль- | ||||||||
| них членів, тобто серед елементів bi. | ||||||||
| Зауваження 3. Для спрощення обчислень в якості ключового | ||||||||
| елемента доцільно вибирати найменший і не обов'язково a11 . | ||||||||
| Приклад 3.Розв’язати методом Жордана-Гаусса систему лі- | ||||||||
| нійних рівнянь: |
| 2 x1 − x2 + 3 x3 = 5 , | ||
| =−3, | ||
| x1 − 4 x2 + 2 x3 | ||
| = 4. | ||
| 3 x1 + 2 x2 + x3 |
Розв’язування. Складемо таблицю із коефіцієнтів,які стоятьбіля невідомих і вільних членів. Стовпець Σ є контрольним.
| № таблиці | x1 | x2 | x3 | bi | Σ | ||||||||||||||||
| -1 | |||||||||||||||||||||
| ×(-2), (-3) | |||||||||||||||||||||
| -4 | -3 | -4 | |||||||||||||||||||
| ×(-1) | |||||||||||||||||||||
| -1 | |||||||||||||||||||||
| -4 | -3 | -4 | |||||||||||||||||||
| -5 | ×(- | ||||||||||||||||||||
| 2), (5) | |||||||||||||||||||||
| -7 | -11 | -17 | |||||||||||||||||||
| ×(- | ) | ||||||||||||||||||||
| -42 | -63 | ||||||||||||||||||||
| -21 | |||||||||||||||||||||
| -1 | ×(-10), (7) | ||||||||||||||||||||
Рядки цих таблиць заповнювались в такій послідовності.
Таблиця 1. За ключовий елемент вибрано коефіцієнт біляx1другого рівняння, тобто число “1”.
Таблиця 2.
1 рядок: елементи другого рядка табл.1 множимо на “-2” і до-даємо до відповідних елементів першого рядка;
2 рядок : перенесено без зміни з таблиці 1.
3 рядок: елементи другого рядка табл. 1 множимо на “-3” і додаємо до відповідних елементів третього рядка.
За ключовий елемент в табл.2 вибираємо число “-1”, яке зна-ходиться в першому рядку.
Таблиця 3.
1 рядок: елементи першого рядка табл.2 множимо на “-1”.
2 рядок: елементи першого рядка табл.3 множимо на “-2” і додаємо до відповідних елементів другого рядка табл.2.
3 рядок: елементи першого рядка табл. 3 множимо на “5” і додаємо до відповідних елементів третього рядка табл.2.
За ключовий елемент цієї таблиці вибираємо число “-21”.
Таблиця 4.
3 рядок: елементи третього рядка табл.3 ділимо на “-21”.
1 рядок: елементи третього рядка табл.4 множимо на “7” і додаємо до відповідних елементів першого рядка табл.3.
2 рядок:елементи третього рядка табл. 4 множимо на “-10” і додаємо до відповідних елементів другого рядка табл.3.
Із останньої таблиці 4 випливає, що x1= −1, x2= 2, x3=3.
Читайте також:
- D) методу мозкового штурму.
- H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
- I Метод Шеннона-Фано
- I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
- I. Метод рiвних вiдрiзкiв.
- VII. Нахождение общего решения методом характеристик
- А. науковий факт, b. гіпотеза, с. метод
- Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
- Агрегативна стійкість, коагуляція суспензій. Методи отримання.
- Агресивний тип дивідендної політики включає метод стабільного приросту дивідендів і метод постійного коефіцієнта виплат.
- АгротехнІЧНИЙ метод
- Адаптовані й специфічні методи дослідження у журналістикознавстві
| <== попередня сторінка | | | наступна сторінка ==> |
| Метод Гаусса | | | Довільні системи лінійних алгебраїчних рівнянь |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |