Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

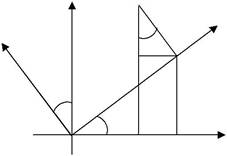
Поворот осей координат

Розглянемо тепер випадок,

у α

М2 1

1 ^B

О М₁ A х

Мал.65

коли нова система координат 0₁ x₁ y₁ одержується із старої

системи координат шляхом повороту її навколо початку координат 0 на кут α

(мал.65).

Нехай координати довільної точки M в старій системі координат 0 xy є

( x , y ) ,а в новій системі ко-

ординат 0 x₁y₁ є ( x₁, y₁).

Відлік кута α повороту про-водиться в напрямі, протилежному рухові годинникової стрілки.

Із малюнка 65 видно, що OM₁=x, MM₁=y, OM₂=x₁, MM₂=y₁,

Для відрізків 0 A, 0 M₁, M₁A, а також для відрізків

MM₁ , M₁ B, MB справедливі рівності

0 M₁ = 0 A − M₁ A = 0 A − BM₂ ,

= + = +

M₁ M M₁ B BM AM₂ BM .

Із прямокутних трикутників 0 M₂A і BMM₂

0 A = 0 M₂ cos α= x₁ cos α , AM₂ = 0 M₂ sin α= x₁ sin α , BM = MM₂ cos α= y₁ cos α , BM₂ = MM₂ sin α= y₁ sin α .

(2.146)

одержуємо

Підставимо знайдені значення 0 A, AM₂, BM , BM₂ в рівності

(2.146), і одержимо формули переходу від старих координат до но-вих при повороті осей на кут α :

x = x₁ cos α − y₁ sin α ,	(2.147)

y = x₁ sin α+ y₁ cos α .
Тепер, щоб виразити нові координати x₁ і	y₁ точки М через

старі координати x , y можна із системи (2.147) двох рівнянь з дво-ма невідомими знайти x₁ та y₁.

Оскільки, формули для нових координат можна одержати по другому: так як нова система координат одержалася із старої систе-ми поворотом на кут α , то стара система одержиться поворотом осей на кут (- α ). Значить в рівняннях (2.147) можна поміняти міс-цями старі і нові координати, замінивши однозначно α на (- α ), то одержимо

	x₁		= x cos α+ y sin α ,			(2.148)
		=− x sin α+ y cos α .
	^y1
Приклад	1.		Який	вигляд	буде	мати	крива
x² + 2 x − y² − 4 y − 7 = 0 ,	якщо за нові осі координат взяти прямі,

які проходять через точку 0₁( −1,−2 ) і паралельні старим осям ко-ординат.

Розв’язування. За формулами(2.145)маємо,що	x = x₁	− 1
	.
		y = y₁	− 2
Підставивши x та	y в рівняння кривої,	одержимо

( x₁ − 1 )² + 2( x₁ − 1 ) − ( y₁ − 2 )² − 4( y₁ − 2 ) − 7 = 0. Після спрощення

одержимо x₁² − y₁² = 4 або	x₁²	−	y₁²	= 1.


Нове рівняння лінії є рівностороння гіпербола.
Приклад	2.Який	вигляд прийме рівняння	гіперболи
x² − y² = 4 ,якщо осі координат повернути на кут(− 45⁰ ) ?
Розв’язування. Оскільки гіпербола x² − y² = 4 є рівносторон-
ньою, то y = x	і y = − x є асимптотами цієї гіперболи.	Приймемо

асимптоти гіперболи за нові осі координат, оскільки вони взаємопе-рпендикулярні, бо добуток їх кутових коефіцієнтів дорівнює (-1).

Замінимо x та y за формулами (2.147) , де α = −45⁰ , маємо

x = x₁ cos( −45⁰ ) − y₁ sin( −45⁰ ) =

( x₁ + y₁ ),

⁰ ) =

y = x₁ sin( −45

) + y₁ cos( −45

( y₁ − x₁ ).

Заміняючи x та

y в рівнянні гіперболи,одержимо

( x₁ + y₁

)² −

( y₁ − x₁ ) = 4 ,

або

після спрощень маємо

x₁ y₁ = 2; тобто

y₁ =

^x1

Це є гіпербола, яку вивчають у шкільному курсі математики, і яка задає обернено пропорційну залежність.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Перенесення початку координат	\|	Полярна система координат

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.