Полярна система координат

М Найбільш важливою після пря-

_ρмокутної системи координат є полярна система координат. До цього положен-

О	φ	Р	ня точки	на площині ми визначали
	Мал.66	двома числами (координатами) в пря-

			мокутній	системі координат, але це

можна однозначно визначити за допомогою полярної системи коор-динат. Вона складається із деякої точки 0 , яка називається полюсом і променя 0 P , який виходить із цієї точки, який називається поляр-ною віссю (мал. 66). Крім цього задається одиниця масштабу.

Нехай точка М довільна точка площини, а ρ віддаль цієї точ-ки від точки 0 , а ϕ це кут, на який потрібно повернути полярну вісь

для суміщення з променем 0 M .

Полярними координатами точки M називаються числа ρ і ϕ . Число ρ вважається першою координатою і називається поляр-ним радіусом, а число ϕ - другою координатою і називається поля-рним кутом. Точка M з полярними координатами позначається так

M ( ρ ,ϕ ).

Полярний радіус може змінюватися в межах: 0 ≤ ρ < + , а полярний кут в межах: 0 ≤ ϕ < 2π; при цьому відлік полярного кута проводиться від полярної осі проти годинникової стрілки.

Між координатами точки у полярній системі координат та її координати в декартовій системі існує простий зв’язок.

Візьмемо вісь 0 x декартової системи координат за полярну вісї полярної системи, а початок декартової системи приймемо за

у М полюс полярної системи координат.

Нехай точка M має прямокутні коор-

_ρ 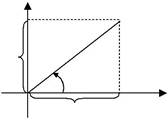динати x та y і полярні координати ρ

у та ϕ (мал.67). Як видно з мал.67, має-

φ х мо

х Мал.67 x =ρ cos ϕ ,

(2.149)

y =ρ sin ϕ.

Формули (2.149) виражають прямокутні координати через по-

лярні.

Якщо піднести до квадрату обидві частини рівностей (2.149) і

додати, то одержимо x² + y² = ρ², або ρ = x² + y² . Якщо ж поді-

лити другу рівність на першу в (2.149), то дістанемо tgϕ = y .

Формули x

ρ = x + y

(2.150)

tgϕ= y

x

визначають полярні координати через декартові. При визначенні полярного кута слід враховувати знаки x та y , користуючись фор-

мулами (2.149).

Приклад 1.Дано прямокутні координати точки(1;1).Знайтиїї полярні координати, вважаючи, що полюс суміщений з початком додатної півосі абсцис.

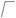
Розв’язування. За формулами(2.150)маємоρ= 2 , tgϕ= 1.

Згідно другої рівності ϕ = ^π , так sin x = 1 > 0 і y = 1 > 0.

Розглянемо деякі криві в полярній системі координат. 1) Спіраль Архімеда.

Ця крива визначається рівнянням r = aϕ

Вигляд спіралі Архімеда має у

пружина в годиннику(мал.68).

х

Мал.68

2) Лемніската Бернуллі. у

Рівняння цієї кривої в полярній

системі координат є

r ² = a² sin 2ϕ. Графік цієї кри-

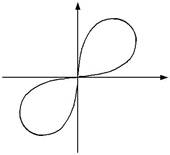
вої зображений на мал. 69. х

Мал.69

Читайте також:
Active-HDL як сучасна система автоматизованого проектування ВІС.
II. Бреттон-Вудська система (створена в 1944 р.)
IV. Система зв’язків всередині центральної нервової системи
IV. УЗАГАЛЬНЕННЯ І СИСТЕМАТИЗАЦІЯ ВИВЧЕНОГО
The educational system of Great Britain (Система освіти Великобританії)
V. Систематизація і узагальнення нових знань, умінь і навичок
VI. Система навчаючих завдань для перевірки кінцевого рівня завдань.
VI. Система навчаючих завдань для перевірки кінцевого рівня завдань.
VI. Узагальнення та систематизація знань
VII. Закріплення нового матеріалу і систематизація знань.
Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
Автоматизована система аудита (system update)

Переглядів: 1187

<== попередня сторінка | наступна сторінка ==>

Поворот осей координат | Розділ 3. ВСТУП У МАТЕМАТИЧНИЙ АНАЛІЗ

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.006 сек.