
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Нтарних функцій, називаються елементарними функціями.
| 2 cos | − tgx | |||
| Наприклад, y = sin2( x2 + x − 5 ) + | x | |||
| + arcsin 2 x + 3 | ||||
| x + | ||||
| sin x |
 - елементарна функція.
- елементарна функція.
Елементарні функції поділяються на такі класи:
1)Цілі раціональні функції:
Цілі раціональні функції – це функції вигляду
y = a0 xn + a1 xn− 1 + ...+ an ,де ak ( k = 0 ,1,2,...,n ) −сталі дійсні числа.
Такі функції називаються ще многочленами, а числа ak - коефіцієн-тами многочлена; якщо a0 ≠ 0 , то число n називають степенем
многочлена.
2) Раціональні функції:
Раціональні функції – це функції вигляду
| y = | a0 xn + a1 xn− 1 | + ... + an− 1 x + an | , тобто це частка двох цілих | |||
| b | xm + b xm − 1 | + ... + b | x + b | |||
| m − 1 | m | |||||
раціональних функцій (многочленів).
Якщо m ≠ 0 , b0 ≠ 0 , то раціональна функція називається
дробово-раціональною.
3)Ірраціональні функції:
Ірраціональні функції - це функції, які задані за допомогою суперпозицій раціональних функцій, степеневих функцій з раціона-льними показниками і чотирьох арифметичних дій, застосованих

| скінчене число раз. Наприклад, | y = 3 | x + 1 | - ірраціональна фун- | |||||||||
| x5 + | ||||||||||||
| x | ||||||||||||
| кція . | 4) Алгебраїчні функції: | |||||||||||
| Функція | y від x ( y = y( x )) називається алгебраїчною,якщо | |||||||||||
| вона задовольняє рівняння | ||||||||||||
| P ( x )yn + P ( x )yn−1 + ...+ P | −1 | y + P ( x ) = 0, де Pk(x),( k = 0 ,1,2,...,n ) | ||||||||||
| n | n | |||||||||||
| - алгебраїчні многочлени від x . | ||||||||||||
| Всяка | раціональна | функція | є | алгебраїчною, | оскільки | |||||||
| P ( x )y + P ( x ) = 0 ,де P ( x)= b xm + ...+b | , | P ( x ) =−( a xn + ...+ a | n | ). | ||||||||
| m |
5)Трансцендентні функції:
Елементарні функції, які не є алгебраїчними, називаються трансцендентними елементарними функціями. Можна показати, що тригонометричні, обернено тригонометричні, показникова і логари-фмічна функції є трансцендентними елементарними функціями.
6) Деякі неелементарні функції:
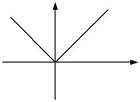
1. y = x - абсолютне значення, або


модуль,числа
 y
y
O x
| 2. y = [ x ] – ціла частина числа | y | |||||||||||
| 4 | ||||||||||||
| 3 | ||||||||||||
| 2 | ||||||||||||
| 1 | ||||||||||||
| -2 -1 O | -1 | 2 3 4 | x | |||||||||
| -2 | ||||||||||||
| y | ||||||||||||
| 3. y = { x} – дробова частина чис- | 1 | |||||||||||
| ла | ||||||||||||
| -1 | O | 1 | 2 | x | ||||||||
| 1, x > 0 , | y | |||||||||||
| 4. y = sign x = − 1, x < 0 , | ||||||||||||
| 0 , x = 0 | ||||||||||||
| -2 | -1 | O | 1 | 2 | x | |||||||
| - знак числа | ||||||||||||
| 2.3. Криві попиту і пропозиції. Точка рівноваги | ||||||||||||
| Розглядаючи попит Q і пропозицію | S в залежності від ціни |
P на вироблений товар,зрозуміло,що чим менша ціна на товар,тобільший попит при певній купівельній спроможності населення , і навпаки, якщо ціна на товар зростає, то пропозиція зростає.
| Як правило, | залежність попиту Q від ціни P | має вигляд: | ||
| Q = P α+ c ,α< 0 , | c = const , | а залежність пропозиції S | від ціни P | |
| має вигляд: S = P α + d , | α ≥ 1, | d = const . | ||
| Константи c | і d | називаються екзогенними величинами і за- | ||
лежать від зовнішніх причин ( благополуччя населення, політичної ситуації, пори року і т.д.).
Графіки даних функцій мають вигляд:

Р
Q
Р
Q S
P0
S0,Q0 S,Q
Р
S
При розв’язуванні економічних задач цікаво знати умову рівнова-
| ги | попиту | і | пропозиції |
| ( Q( Р ) = S( Р ) , | тобто | рівноваж- |
ну ціну P0) .
§ 3. Границя числової послідовності
3.1. Числова послідовність
Означення1. Кожна функція f визначена на множині на-туральних чисел N ={1 ,2,3,...,n,...} називається числовою послі-
довністю.
Запишемо значення функції f :
| f ( 1 ), f ( 2 ), f ( 3 ),..., f ( n ),... | (3.1) |
| Введемо позначення | |
| xn = f ( n ) ,n ∈N. | (3.2) |
Отже, числову послідовність (3.1) можна записати так : x1 , x2 , x3 ,..., xn ,..., або скорочено
| ( xn ),n ∈N , | (3.3) |
| де x1, x2,... називають членами послідовності, а xn | - “енним ” або |
| загальним членом числової послідовності. | |
| Якщо задана послідовність у такому вигляді | |
| xn , n ∈N , | (3.4) |
то задано закон утворення її членів, тобто надаючи номеру n значень 1,2,3,... можна однозначно визначити всі її члени
x1,x2,…і навпаки,якщо задано послідовність її першими членами,то можна завжди записати її загальний член. Наприклад, нехай
| 1) xn = | , n ∈N . | ||||||
| n | |||||||
| Маємо x1 | = 1, x2 | = | , | ||||
2) x1 = 1 , x2 = 2 , x3 =

 23
23
Звідси випливає, що xn
| x3 | = | ,…….., xn | = | ,… | |||
| n | |||||||
3 ,….
 4
4
= n , n ∈N . n + 1

Як вже зазначалося вище, для задання послідовності необхідно знати правило, за яким кожному значенню n ставиться у відповідність дійсне число xn=f(n). Таке правило може бути задане за допомогою фо-рмули, як це зроблено у наведених вище прикладах. Проте є інші спо-соби задання послідовностей. Наприклад, візьмемо за (xn)n -ну цифру розкладу числа π у нескінчений десятковий дріб. Матимемо послідов-
ність 3,1,4,1,…
Тут правило відповідності задано словесно.
Іноді при заданні послідовності задається її перший член і прави-ло утворення n-го члена за допомогою попередніх членів. Такий спосіб називається рекурентним. Наприклад, нехай перший член послідовнос-ті дорівнює 2, а кожний наступний дорівнює попередньому, помноже-
ному на 10. Тоді xn+1=10xn, x1=2,n ∈N .
Серед числових послідовностей в окремий клас виділяють так звані монотонні послідовності, що об’єднують в собі зростаючі, спадні, неспадні, незростаючі послідовності.
Означення2. Послідовність (xn) називається зростаючою, якщо кожний її наступний член більший від попереднього, тоб-то xn+ 1 > xn для кожного n .
Наприклад, послідовність, 1,22,32,...,n2,... є зростаюча.
Означення3. Послідовність (xn) називається неспадною, якщо xn+ 1 ≥ xn для кожного n .
Наприклад, послідовність 1,1,1,2,2,... є неспадна.
Означення4. Послідовність (xn) називається спадною, якщо xn+ 1 < xn для кожного n .
Наприклад, послідовність 1,1,1,...,1,... є спадна.


 2 3 n
2 3 n
Означення5. Послідовність ( xn ) називається незростаю-чою, якщо xn+ 1 ≤ xn для кожного n .
Для дальшого вивчення числових послідовностей необхідно ввести в розгляд такі арифметичні операції над числовими послідо-вностями: додавання, віднімання, множення та ділення.
Нехай маємо дві послідовності
x1 , x2 ,..., xn ,...
y1` , y2 ,..., yn ,...
Читайте також:
- Бюджетні установи отримують кошти на своє функціонування з бюджету виключно на основі фінансових документів, які називаються кошторисами.
- Важкість праці: Динамічні, статичні навантаження. Напруженість праці. Увага, напруженість аналізаторних функцій, емоційна та інтелектуальна напруженість, монотонність праці.
- Види документарних акредитивів в міжнародній практиці
- Визначення. Матриці, отримані в результаті елементарного перетворення, називаються еквівалентними.
- Визначення. Точки максимуму й мінімуму функції називаються точками екстремуму.
- Визначення. Числа й називаються комплексно спряженими.
- Витрати одного блага, виражені в кількості іншого блага, яким довелося знехтувати (пожертвувати) називаються альтернативними витратами.
- За обліковими функціями.
- Завдання 4. Записати коментарі до малюнків. Як називаються твори, ілюстрації до яких представлені нижче? Який це жанр?
- Залежно від джерел інформації, яка використовується при здійсненні контрольних функцій, внутрішній контроль поділяється на документальний і фактичний.
- Класифікація елементарних частинок
- Лінійна регресія за допомогою функцій, лінійного тренду та пакета аналізу
| <== попередня сторінка | | | наступна сторінка ==> |
| Функцією від функції. | | | Тоді додавання, віднімання та множення двох послі-довностей виконуються додаванням, відніманням та мно-женням відповідних членів цих послідовностей. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |