Критерій розщеплення

Процес конструювання дерева рішень

Нагадаємо, що розглянута нами задача класифікації ставиться до стратегії навчання з вчителем, іноді називаного індуктивним навчанням. У цих випадках всі об'єкти тренувального набору даних заздалегідь віднесені до одного з визначених класів.

Алгоритми конструювання дерев рішень складаються з етапів "побудова" або "створення" дерева (tree building) і "скорочення" дерева (tree pruning). У ході створення дерева вирішуються питання вибору критерію розщеплення і зупинки навчання (якщо це передбачено алгоритмом). У ході етапу скорочення дерева вирішується питання відсікання деяких його гілок.

Розглянемо ці питання детальніше.

Процес створення дерева відбувається зверху вниз, тобто є спадним. У ході процесу алгоритм повинен знайти такий критерій розщеплення, іноді також називається критерієм розбивки, щоб розбити множину на підмножини, які б асоціювалися з даним вузлом перевірки. Кожен вузол перевірки повинен бути позначений певним атрибутом. Існує правило вибору атрибута: він повинен розбивати вихідну множину даних таким чином, щоб об'єкти підмножин, що одержуються у результаті цієї розбивки, були представниками одного класу або ж були максимально наближені до такої розбивки. Остання фраза означає, що кількість об'єктів з інших класів, так званих "домішок", у кожному класі повинно прямувати до мінімуму.

Існують різні критерії розщеплення. Найбільш відомі – міра ентропії і індекс Gini.

У деяких методах для вибору атрибута розщеплення використовується так названа міра інформативності підпросторів атрибутів, що ґрунтується на ентропійному підході і відома за назвою "міра інформаційного виграшу" (information gain measure) або міра ентропії.

Інший критерій розщеплення, запропонований Брейманом (Breiman) і ін., реалізований в алгоритмі CART та називається індексом Gini. За допомогою цього індексу атрибут вибирається на підставі відстаней між розподілами класів.

Якщо дано множину T, що включає приклади з n класів, індекс Gini, тобто gini(T), визначається по формулі:

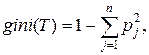
де T – поточний вузол, p_j – імовірність класу j у вузлі T, n – кількість класів.

Велике дерево не означає, що воно "підходяще"

Чим більше окремих випадків описано в дереві рішень, тим менша кількість об'єктів попадає в кожен окремий випадок. Такі дерева називають "гіллястими" або "рунистими", вони складаються з невиправдано великої кількості вузлів і гілок, вихідна множина розбивається на велику кількість підмножин, що складаються з дуже малого числа об'єктів. У результаті "переповнення" таких дерев їх здатність до узагальнення зменшується, і побудовані моделі не можуть давати вірні відповіді.

У процесі побудови дерева, щоб його розміри не стали надмірно великими, використовують спеціальні процедури, які дозволяють створювати оптимальні дерева, так називані дерева "підходящих розмірів" (Breiman, 1984).

Який розмір дерева може вважатися оптимальним? Дерево повинно бути досить складним, щоб враховувати інформацію з досліджуваного набору даних, але одночасно воно повинно бути досить простим [39]. Інакше кажучи, дерево повинно використовувати інформацію, що поліпшує якість моделі, і ігнорувати ту інформацію, що її не поліпшує.

Отут існує дві можливі стратегії. Перша складається в нарощуванні дерева до певного розміру відповідно до параметрів, заданими користувачем. Визначення цих параметрів може ґрунтуватися на досвіді та інтуїції аналітика, а також на деяких "діагностичних повідомленнях" системи, що конструює дерево рішень.

Друга стратегія складається у використанні набору процедур, що визначають "підходящий розмір" дерева, вони розроблені Бріманом, Куілендом та ін. в 1984 році. Однак, як відзначають автори, не можна сказати, що ці процедури доступні недосвідченому користувачеві.

Процедури, які використовують для запобіганню створенню надмірно великих дерев, включають: скорочення дерева шляхом відсікання гілок; використання правил зупинки навчання.

Слід зазначити, що не всі алгоритми при конструюванні дерева працюють по одній схемі. Деякі алгоритми включають два окремих послідовних етапи: побудова дерева і його скорочення; інші чергують ці етапи в процесі своєї роботи для запобігання нарощування внутрішніх вузлів.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Переваги дерев рішень	\|	Алгоритми

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.014 сек.