
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Тема 4. Теорія двоїстості та аналіз лінійних оптимізаційних задач
До кожної задачі лінійного програмування можна скласти двоїсту. Значення цільових функцій прямої та двоїстої задачі обов’язково співпадають, однак вони протилежно направлені (перша теорема двоїстості).
Спочатку треба перевірити, що пряма задача приведена до стандартного вигляду. Якщо цільова функція прямої задачі прямує до максимуму, потрібно, щоб всі обмеження мали знаки ≤ або =, а якщо до мінімуму, то ≥ або =. Інакше необхідно помножити відповідне обмеження на -1.
Якщо пряма задача ЛП має вигляд
Z = c1x1 + c2x2 + … + cnxn ® max
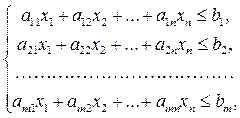
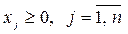 ,
,
то двоїстою до неї буде:
F = b1y1 + b2y2 + … + bmym ® min

 .
.
Приклад 4.1
Скласти двоїсту до задачі лінійного програмування:
Z = 6x1 – 4x2 ® min

Розв’язання
Помножимо другу нерівність на -1, щоб звести задачу до стандартного вигляду. Для зручності можна написати цільову функцію після системи обмежень. Стовпчики прямої задачі стануть рядочками двоїстої, а рядочки – стовпчиками. Знаки нерівностей в обмеженнях зміняться на протилежні.

Z = 6x1 – 4x2 ® min
Двоїста задача виглядатиме наступним чином:
F = 2y1 – 8y2 ® min

Існують симетричні та несиметричні двоїсті пари задач лінійного програмування. У симетричних задачах усі обмеження прямої та двоїстої задач є нерівностями, а змінні обох задач можуть мати лише невід’ємні значення. Якщо хоча б одне обмеження прямої задачі є рівнянням, пара задач є несиметричною. У цьому разі відповідні змінні двоїстої задачі можуть приймати будь-яке значення.
Розглянемо економічну інтерпретацію двоїстої задачі.
Приклад 4.2
Підприємство виготовляє 4 види продукції, використовуючи для цього три види ресурсів 1, 2, 3 (табл. 4.1). Визначити план виробництва продукції, що забезпечує підприємству найбільший дохід. Ціна одиниці продукції становить відповідно 7, 4, 2 та 1 у. о.
Таблиця 4.1
Норми витрат ресурсів на одиницю продукції та їх запаси
| Ресурс | Норма витрат на одиницю продукції, за видами | Запас ресурсу | |||
| А | В | С | D | ||
Записати економіко-математичні моделі прямої та двоїстої задач, симплекс-методом визначити їх оптимальні плани, провести економічний аналіз.
Розв’язання
Складемо економіко-математична модель прямої задачі:



Остання симплекс-таблиця прямої задачі має наступний вигляд (табл. 4.2):
Таблиця 4.2
Застосування симплекс-методу – остання ітерація
| Базис | Сбаз | План | |||||||
| х1 | х2 | х3 | х4 | х5 | х6 | х7 | |||
| x2 | 1/4 | -1/4 | 1/2 | -3/4 | |||||
| x1 | 1/2 | 1/2 | 1/2 | ||||||
| x7 | -1/2 | -1/2 | -1 | 1/2 | |||||
| Zj – Cj ≥ 0 | 21/2 | 11/2 |
Отже, підприємству доцільно виготовляти 70 од. продукції А та 50 од. продукції В, що забезпечить дохід 650 у. о.
Економіко-математична модель двоїстої задачі наступна:

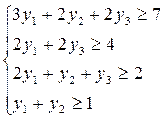

Змінна y1двоїстої задачі пов’язана з x5прямої, y2– з х6, y3– з х7.
Таким чином, оптимальний план двоїстої задачі y1= 1½, y2=2, y3=0. Третя сировина не повністю використовується у виробництві, тому є недефіцитною.
Оптимальні значення цільових функцій прямої та двоїстої задачі однакові, тому мінімальна вартість ресурсів, що використовуються для виробництва продукції становить 285 у. о.
Питання для самостійного вивчення: двоїсті оцінки і дефіцитність ресурсів, інтервали стійкості двоїстих оцінок стосовно зміни запасів дефіцитних ресурсів.
Читайте також:
- ABC-XYZ аналіз
- E) теорія раціонального вибору.
- I етап. Аналіз впливу типів ринку на цінову політику.
- I. Теорія граничної продуктивності і попит на ресурси
- II. Багатофакторний дискримінантний аналіз.
- II. Критерій найбільших лінійних деформацій
- III етап. Аналіз факторів, що визначають цінову політику підприємства.
- SWOT-аналіз у туризмі
- SWOT-аналіз.
- Tема 4. Фації та формації в історико-геологічному аналізі
- V теорія граничної корисності визначає вартість товарів ступенем корисності останньої одиниці товару для споживача.
- V. Нюховий аналізатор
| <== попередня сторінка | | | наступна сторінка ==> |
| Тема 2. Оптимізаційні економіко-математичні моделі | | | Тема 7. Аналіз та управління ризиком в економіці. Визначення ризику, види ризиків в економіці |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |