• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Побудова лекальних кривих

Лекальними називаються криві, які креслять за допомогою лекал за попередньо знайденими окремими точками.

До лекальних належать лінії другого порядку – еліпс, парабола, гіпербола, а також інші закономірні і довільні лінії.

5.2.1. Побудова еліпса за двома його осями

Еліпс, який задається великою та малою осями, є геометричним місцем вершин прямих кутів прямокутних трикутників, гіпотенузи яких по довжині дорівнюють різниці радіусів двох концентричних кіл, побудованих на цих осях як на діаметрах, а катети відповідно паралельні цим осям.

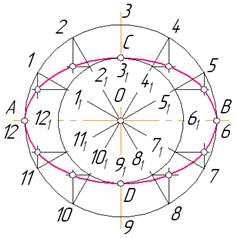
Задано осі еліпса – велику АВ і малу СD. З центра еліпса (рис. 5.4) описують два кола, діаметри яких дорівнюють великій і малій осям еліпса. Коло більшого діаметру ділять на однакову кількість рівних частин, наприклад на дванадцять. З'єднують точки поділу з центром О, розділивши таким чином коло меншого діаметру на таку ж кількість частин.

З точок поділу кола більшого діаметру (за винятком точок 3, 6, 9, 12) проводять прямі, паралельні малій осі еліпса СD, а з точок поділу кола меншого діаметру (за винятком точок С і D) - паралельні великій осі АВ. Перетин відповідних пар цих прямих визначає ряд точок, з’єднавши які плавною кривою, одержують шуканий еліпс.

Рис. 5.4. Побудова еліпсу	Рис. 5.5. Побудова параболи

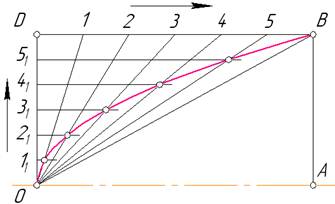
5.2.2. Побудова параболи за вершиною О, віссю ОА і довільною точкою В, що лежить на обрисі параболи.

Будують прямокутник ОDВА, вершинами якого є задані точки О і В (рис. 5.5). Відрізки ОD і DВ ділять на однакову кількість рівних частин, наприклад на шість. Точки поділу нумерують у напрямах, показаних стрілками. Вершину О сполучають з точками 1, 2, 3, 4, 5, а через точки 1₁, 2₁, 3₁, 4₁, 5₁ проводять прямі, паралельні осі симетрії ОА. Перетин однойменних прямих дає точки, які належать параболі.

5.2.3. Побудова гіперболи за заданою вершиною А і точкою Р, що лежить на обрисі гіперболи.

З точки Р (рис. 5.6) проводять перпендикуляр до дійсної осі гіперболи АВ і будують прямокутник ABРN. Сторони прямокутника PN і PB ділять на однакову кількість рівних частин, наприклад на чотири. Відкладають відрізок ОА=АВ. Проводять два пучка променів: з точки А до точок поділу 1, 2, 3 і з точки О до точок поділу 1₁, 2₁, 3₁. На взаємних перетинах цих променів отримують шукані точки А₁, А₂, А₃ та з’єднують їх за допомогою лекала.

Рис. 5.6. Побудова гіперболи	Рис. 5.7. Побудова спіралі Архімеда

5.2.4. Побудова спіралі Архімеда за заданим центром О і кроком спіралі а.

З центра О (рис. 5.7) описують коло радіусом R=а. Відрізок ОА та коло ділять на однакову кількість рівних частин, наприклад на вісім. Точки шуканої спіралі Архімеда дістають в перетинах концентричних кіл, проведених із центра О радіусами О1, О2, О3, О4,… з променями О1₁, О2₁, О3₁,…, проведеними через відповідні точки поділу кола. Одержані точки спіралі А₁, А₂, А₃,… сполучають під лекало.

5.2.5. Побудова синусоїди.

Коло діаметром d та відрізок АВ, довжина якого дорівнює довжині кола pd, ділять на однакову кількість рівних частин, у даному разі – на дванадцять (рис. 5.8). Після цього через точки поділу кола проводять прямі, паралельні відрізку АВ, до перетину їх з відповідними прямими, проведеними з точок 1₁…11₁ перпендикулярно відрізку АВ. Одержані точки синусоїди А₁…А₁₁ сполучають під лекало.

Рис. 5.8. Побудова синусоїди

5.2.6. Побудова циклоїди за заданим діаметром твірного кола.

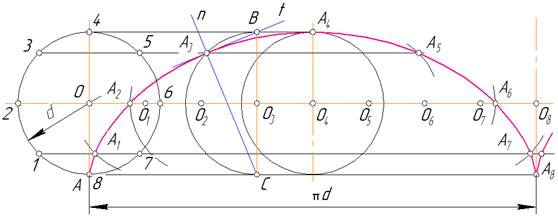
На горизонтальній прямій ОО₈ (рис. 5.9), яка проходить через центр О твірного кола, відкладають його довжину, розраховану за формулою L = pd, де d – діаметр кола. Цей відрізок і твірне коло ділять на однакову кількість рівних частин, наприклад на вісім. Із точок 1, 2, 3,… поділу кола проводять горизонтальні прямі. З точок О₁, О₂, О₃,…, як із центрів,

Рис. 5.9. Побудова циклоїди

проводять дуги радіусом d/2 до перетину з відповідною горизонтальною лінією і дістають точки А₁, А₂, А₃,…, що належать циклоїді. Ці точки спочатку сполучають від руки на око плавною лінією, а потім за допомогою лекала.

Нормаль і дотичну до циклоїди в точці А₃ будують так. Визначають положення твірного кола, за яким точка А прийде в точку А₃. Через центр кола О₃ проводять вертикальний діаметр ВС. Пряма СА₃ буде нормаллю п, а ВА₃ – дотичною t до циклоїди в точці А₃.

Читайте також:

1. АСОЦІАЦІЯ. ПОБУДОВА АСОЦІАТИВНОГО КУЩА
2. Бухгалтерські рахунки, їх призначення, функції і побудова
3. Бюджетний устрійпоказує, в який спосіб побудована бюджетна система. Іншими словами,він відображає організацію вертикальної структури бюджету держави за рівнями влади.
4. Визначення практичної придатності побудованої ої регресійної моделі.
5. Д80.Парламент в ЗК.ознаки 81.Побудова та основні ознаки парламенту в ЗК.
6. Дискретні радіодеталі, побудовані на основі провідникових і
7. Емпіричні формули. Побудова формули лінійної залежності методом найменших квадратів
8. Загальна побудова організації контрольного процесу в умовах автоматизованої обробки інформації
9. Загальна схема дослідження функції і побудова її графіка
10. Загальна характеристика формоутворення кривих ліній та кривих поверхонь
11. Задачі інцидентності на кривих поверхнях
12. Зміст і побудова інструкцій

Переглядів: 3709