• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Визначення практичної придатності побудованої ої регресійної моделі.

Практичну придатність побудованої моделі 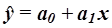можна охарактеризувати за величиною лінійного коефіцієнта кореляції r:

· близькість до одиниці свідчить про хорошу апроксимацію фактичних даних за допомогою побудованої лінійної функції зв'язку ;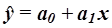

· близькість до нуля означає, що зв'язок між фактичними даними Хі Yне можна апроксимувати як за побудованою, так і будь-якою іншою лінійною моделлю, і, отже, для моделювання зв'язку слід використовувати яку-небудь відповідну нелінійну модель.

Придатність побудованої регресійної моделі для практичного використання можна оцінити і за величиною індексу детермінації R², який показує, яка частина загальної варіації ознаки Y пояснюється в побудованій моделі варіацією чинника X.

У основі такої оцінки лежить рівність R = , а також шкала Чеддока, що встановлює якісну характеристику щільності зв'язку залежно від величини .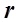

Згідно шкали Чеддока високий ступінь щільності зв'язку ознак досягається лише при >0,7, тобто при >0,7. Для індексу детермінації R²це означає виконання нерівності R² >0,5.

При недостатньо щільному зв'язку ознак X, Y (слабка, помірна, помітна) має місце нерівність 0,7, а отже, і нерівність .

З урахуванням вищесказаного, практична придатність побудованої моделі зв'язку 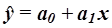оцінюється за величиною R²таким чином:

· нерівність R² >0,5дозволяє вважати, що побудована модель придатна для практичного застосування, оскільки в ній досягається високий ступінь щільності зв'язку ознак Xі Y, при якій більше 50% варіації ознаки Yпояснюється впливом чинника Х;

· нерівність означає, що побудована модель зв'язку практичного значення не має, зважаючи на недостатню щільність зв'язку між ознаками Xі Y, при якій менше 50% варіації ознаки Yпояснюється впливом чинника Х, і, отже, чинник Хвпливає на варіацію Yв значно меншій мірі, ніж інші (невраховані в моделі) чинники.

Значення індексу детермінації R²наводиться в табл. 2.5 в комірці В79 (термін "R -квадрат").

Висновок:

Значення лінійного коефіцієнта кореляції r і значення індексу детермінації R² згідно таблиці. 2.5 рівні: r = 0,352, R²= 0,124. Оскільки 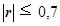і 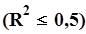, то побудована лінійна регресійна модель зв'язку не придатна для практичного використання.

Читайте також:

1. CMM. Визначення моделі зрілості.
2. I визначення впливу окремих факторів
3. II. Визначення мети запровадження конкретної ВЕЗ з ураху­ванням її виду.
4. II. Мотивація навчальної діяльності. Визначення теми і мети уроку
5. Ocнoвнi визначення здоров'я
6. S Визначення оптимального темпу роботи з урахуванням динаміки наростання втоми.
7. Автокореляція залишків – це залежність між послідовними значеннями стохастичної складової моделі.
8. Алгебраїчний спосіб визначення точки беззбитковості
9. Алгоритм побудови калібрувального графіка для визначення загального білка сироватки крові
10. Алгоритм побудови калібрувального графіка для визначення загального білка сироватки крові
11. Аналіз існуючих виробів та визначення завдань проекту
12. Аналіз результатів практичної діяльності Київського освітньо-методичного центру соціальної роботи

Переглядів: 888