Емпіричні формули. Побудова формули лінійної залежності методом найменших квадратів

При розв'язуванні практичних задач часто виникає ситуація, коли аналітичний вигляд функції не заданий, але ця функція задана таблично, тобто:

x	x₁	x₂	…	x_i	…	x_n
y	y₁	y₂	…	y_i	…	y_n

Такі таблиці отримують в результаті дослідів (експериментів), тому їх називають емпіричними таблицями. За заданою емпірич-ною таблицею потрібно знайти аналітичний вид функції. В загаль-ному випадку це досить складна задача і розв’язується вона неодно-значно. Одним із найбільш поширених методів знаходження аналі-

тичного виду відповідної функції є метод найменших квадратів. Цей метод часто використовується в статистиці та економічних дослі-дженнях.

Розглянемо випадок, коли зв’язок між x і y прямолінійний, тобто y = kx + b .

Нехай задана емпірична таблиця. Розглянемо на площині x0 y

точки M₁ ( x₁ ; y₁ ); M₂ ( x₂ ; y₂ ),..., M_i ( x_i ; y_i ),..., M_n ( x_n ; y_n ).

Оскільки між х і у існує прямолі- у М₃ М_n

нійний зв’язок, то ці точки будуть δn

розміщені на площині хОу так, що М₂ δ₃ δi

через них можна наближено про- δ₂ М₄

вести пряму лінію. Побудуємо від- М_i

х₁ О

повідний малюнок (мал. 12). 2 3х4 i х_n х

Нам відомо, що рівняння цієї δ1 _М₁

прямої буде y = kx + b ,де k і b Мал.12

деякі невідомі параметри. З кожної точки M_i( i = 1,2,...,n ) опусти-

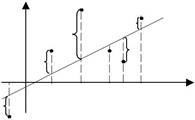мо перпендикуляри на вісь 0 x і продовжимо їх до перетину з пря-мою лінією. Ординати точок перетину з прямою y = kx + b позна-

чимо _i ( i = 1,2,...,n ). Різницю _i − y_i позначимо черезδ_i і назве-

y y

мо її нев’язкою (похибкою). Очевидно, що числа δ_і = i − y_i мо-

y

жуть приймати довільні значення. Складемо суму квадратів нев’язок, тобто:

n

F ( k ,b ) =δ₁² +δ²₂ + ...+δ_n² =∑δ_i² .

i = 1

Тепер сформулюємо задачу: потрібно вибрати положення прямої y = kx + b так, щоб величина F приймала мінімальне зна-

чення. Аналітично цю задачу розв’язуємо так: припустимо, що фун-кція y = kx + b задана. Знайдемо значення нев’язок:

δ₁ = y₁ − y₁ = kx₁ + b − y₁ ;

..............................................

δ_i = y_i − y_i = kx_i + b − y_i ;

.............................................

δ_n = y_n − y_n = kx_n + b − y_n .

Підставимо ці значення δ_i в F ( k ,b ) :

F ( k ,b ) =∑ⁿ (kx_i + b − y_i )² .

i = 1

Таким чином , задача зводиться до знаходження мінімуму фу-нкції F ( k ,b ) відносно змінних k і b. Запишемо необхідну умову

екстремуму:

∂F ( k ,b ) ₌ _{0 ,}

∂k

∂F ( k ,b ) = 0.

∂b

Знайдемо частинні похідні і підставимо їх в рівняння:

∂F ( k ,b ) n

= ∑2( kx_i + b − y_i )⋅ x_i = 0 ,

∂k

i = 1

∂F ( k ,b ) n

=∑2( kx_i + b − y_i ) = 0.

∂b i = 1

Виконавши відповідні елементарні перетворення, в кінцевому

результаті отримаємо систему рівнянь:

n n n

k∑ x _i² + b∑ x _i =∑x_i , y_i ,

i = 1 i = 1 i = 1 .

n n

k∑ x _i + nb =∑ y_i .

i = 1 i = 1

Ця система називається нормальною системою рівнянь методу найменших квадратів.З неї знаходимоkіbі підставляє-мо в формулу y = kx + b. Для практичного розв’язування задач зру-

чно користуватися розширеною емпіричною таблицею, яка одержу-

ється таким чином: до вихідної таблиці додаємо два рядки для x² та xy і один стовпчик,в якому записуємо відповідні суми,що входять

у нормальну систему. В результаті отримаємо таку таблицю:

x x₁ x₂ ... x_n ∑^xi

y y₁ y₂ ... y_n ∑ ^yi

x ...

x₁ x₂ x_n ∑^xi

xy x₁ y₁ x₂ y₂ ... x_n y_n ∑^xi ^yi

Дані останнього стовпчика таблиці підставляємо в нормальну систему рівнянь.

Приклад 1.Дано таблицю

x -1

y -0,9 1,2 2,8 7,1 10,8

Знайти коефіцієнти прямолінійного зв’язку між x і y . Розв’язування. Будуємо розширену таблицю.

x -1

y -0,9 1,2 2,8 7,1 10,8

_x2

xy 0,9 2,8 21,3

За таблицею складаємо систему рівнянь при n = 5 :

36k + 8b = 79,

+ =

K 5b 21.

Домножимо друге рівняння на Одержимо:

23,2k = 45 ,4

+ =

8k 5b 21. Відповідь: y = 1,96 x + 1,06.

(-1,6) і додамо до першого.

k = 1,96

^⇔ b = 1,06.

Читайте також:
VII. Нахождение общего решения методом характеристик
Аверсивную терапію використовують, як правило, при лікуванні алкоголізму, нікотиновій залежності і деяких інших захворювань.
Аналіз фінансової звітності методом коефіцієнтів
Аналіз фінансової незалежності підприємства
АСОЦІАЦІЯ. ПОБУДОВА АСОЦІАТИВНОГО КУЩА
Аспекти незалежності аудиторської професії
Аспекти незалежності аудиторської професії.
Банку за методом кумулятивного гепу, (тис. грн.)
Безпосереднє обчислення з використанням формули Ньютона-Лейбніца.
Бухгалтерські рахунки, їх призначення, функції і побудова
Бюджетний устрійпоказує, в який спосіб побудована бюджетна система. Іншими словами,він відображає організацію вертикальної структури бюджету держави за рівнями влади.
В залежності від джерел сплати

Переглядів: 3460

<== попередня сторінка | наступна сторінка ==>

Рівняння (5.14) називаються рівняннями зв’язку, а відпо-відний екстремум функції називається умовним екстремумом. |

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.