• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Неперервність функції

Функція 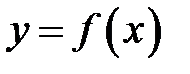називається неперервною в точці 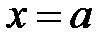, якщо вона визначена в деякому околі точки 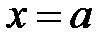і

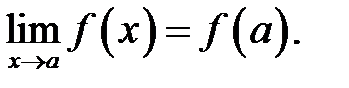
Згідно з означенням границі функції за Коші означення неперервності можна сформулювати так.

Функція 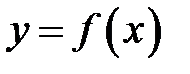називається неперервною в точці 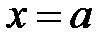, якщо для довільного існує 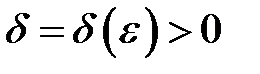таке, що 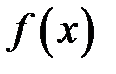визначена в 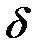-околі 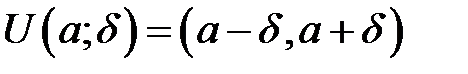і для всіх виконується нерівність

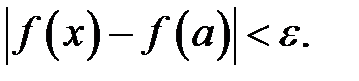
Символічно

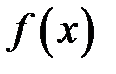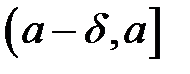Якщо функція визначена на (відповідно на ) і (відповідно 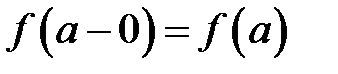), тоді 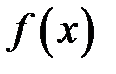називається неперервною справа (відповідно зліва) в точці .

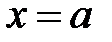Для того, щоб 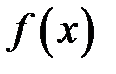була неперервною в точці 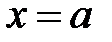, необхідно і достатньо, щоб

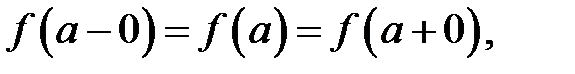
тобто щоб 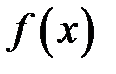була неперервною в цій точці справа і зліва.

Властивості неперервних функцій в точці.

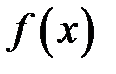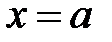1. Якщо функції і неперервні в точці , то

a. ,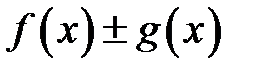

b. ,

c. 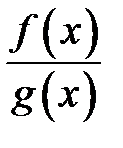при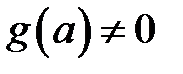

неперервні в точці .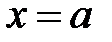

2. Композиція функцій 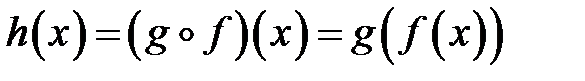неперервна в точці 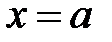, якщо 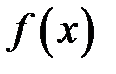неперервна в точці 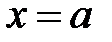, а 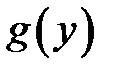неперервна в точці .

3. Кожна елементарна функція, що визначена в околі точки 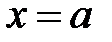, є неперервною в цій точці.

Приклад 1. Довести неперервність функції в точці за означенням неперервності.

Розв’язання. Маємо

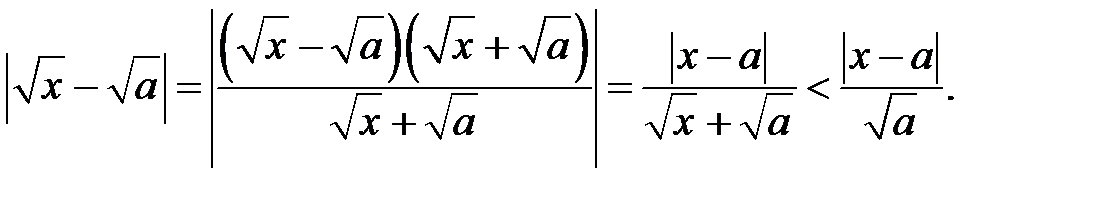
Нехай довільне. Нерівність 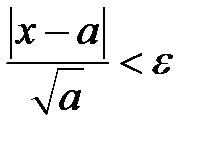рівносильна нерівності 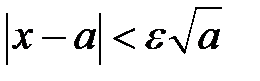. Приймемо 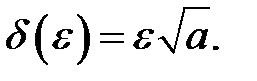Тоді

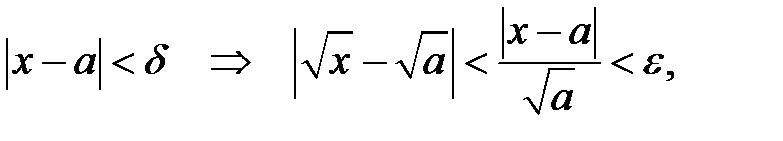
що й доводить неперервність функції в точці

Точки розриву функції

Окіл точки , з якого вилучено саму точку , називається проколеним околом точки і позначається символом 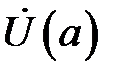. Таким чином,

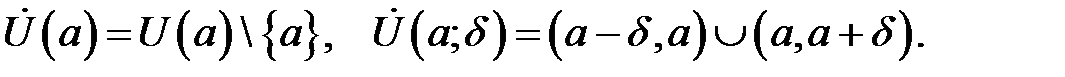
Припустимо, що функція визначена в проколеному околі точки 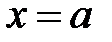і, можливо, в самій цій точці. Якщо точка 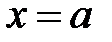не є точкою неперервності функції 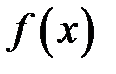, то вона називається точкою розриву функції .

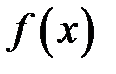1. При цьому, якщо існує 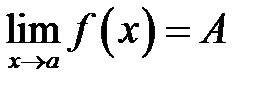, але 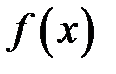невизначена в точці 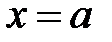, або 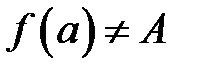, тоді 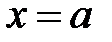називається точкою усувного розриву функції .

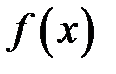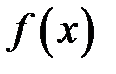(Зауважимо, що якщо покласти , то функція стане неперервною в точці 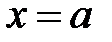, тобто розрив буде усунуто.)

2. Якщо існують скінченні 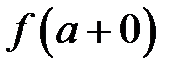та 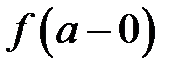, але не виконується одна з умов рівност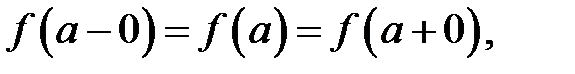і тоді 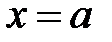називається точкою розриву І роду.

(При цьому кажуть, що функція 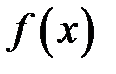в точці 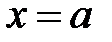має стрибок.)

3. В точці 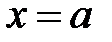не існує принаймні одна з границь 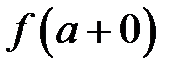, 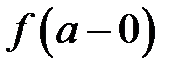або хоча б одна з них нескінченна. Тоді точка 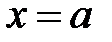називається точкою розриву ІІ роду.

Неперервні функції на множині

Функція 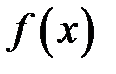називається неперервною на множині 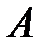, якщо вона неперервна в кожній точці цієї множини.

Якщо не всі точки 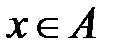входять у множину 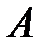разом з деяким околом, то означення трохи змінюється.

Функція 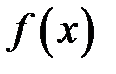, визначена на відрізку 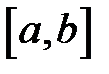, називається неперервною на 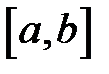, якщо вона неперервна в кожній точці інтервала 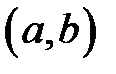, неперервна справа в точці 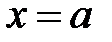і неперервна зліва в точці .

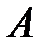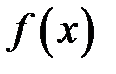Клас неперервних на множині функцій позначається , тобто запис означає, що функція неперервна на множині .

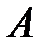Нагадаємо основні властивості неперервних функцій на відрізку.

Теорема 1 (Вейєрштрасса). Якщо функція неперервна на відрізку, то вона обмежена на ньому.

Теорема 2 (Вейєрштрасса). Якщо функція неперервна на відрізку, то вона приймає на ньому найбільше та найменше значення.

Теорема 3 (Больцано-Коші). Якщо функція неперервна на відрізку і на його кінцях приймає значення протилежного знаку, то існує точка всередині цього відрізку, в якій функція дорівнює нулю.

Теорема 4 (Коші). Якщо функція неперервна на відрізку, то вона приймає всі проміжні значення між значеннями функції в кінцях цього відрізка.

Функція називається рівномірно неперервною на множині 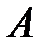, якщо для довільного існує 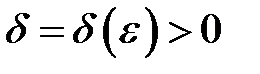таке, що для всіх таких, що , виконується нерівність

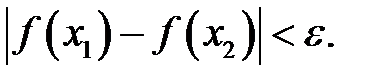
Теорема 5 (Кантора). Якщо функція неперервна на відрізку, то вона також рівномірно неперервна на ньому на ньому.

Кажуть, що функція 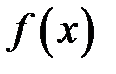строго зростає (відповідно строго спадає) на множині 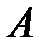, якщо для довільних 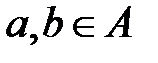таких, що 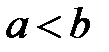, маємо (відповідно ).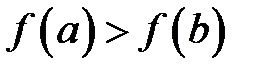

Функції, що строго зростають чи спадають на множині 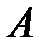, називають строго монотонними на множині .

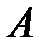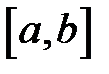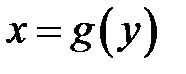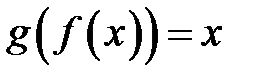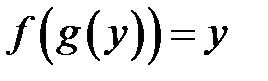Теорема 6 (про існування оберненої функції). Нехай функція неперервна на відрізку та строго монотонна на ньому (наприклад, зростає). Тоді існує єдина функція , яка визначена, строго зростає і неперервна на відрізку така, що для всіх і для всіх 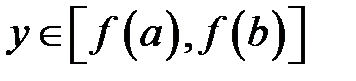, тобто .

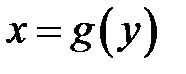Зауважимо, що для строго спадної функції обернена функція визначена на відрізку .

Приклад 2. Довести, що рівняння 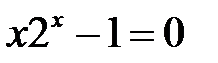має додатний корінь, менший за одиницю.

Розв’язання. Функція неперервна на всій числовій осі, зокрема і на відрізку 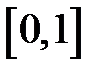. Оскільки , а , то за теоремою Больцано-Коші існує така точка 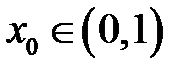, що 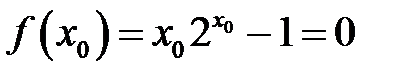, тобто 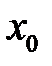— потрібний нам корінь.

Приклад 3. Дослідити на неперервність функцію

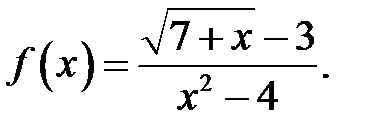
Розв’язання. Область визначення функції

При 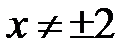функція неперервна на 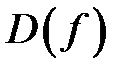як відношення двох неперервних функцій і , які є елементарними. Функція 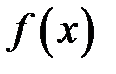визначена в проколеному околі кожної з точок 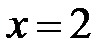та , а в самих точках не визначена, тому ці точки є точками розриву. Вкажемо характер точок розриву. Обчислимо

Аналогічно

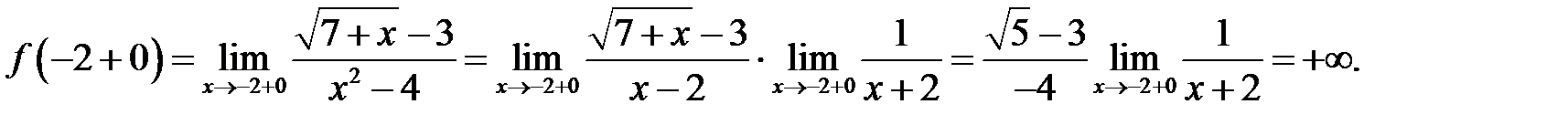Отже, точка є точкою розриву другого роду.

Обчислимо тепер

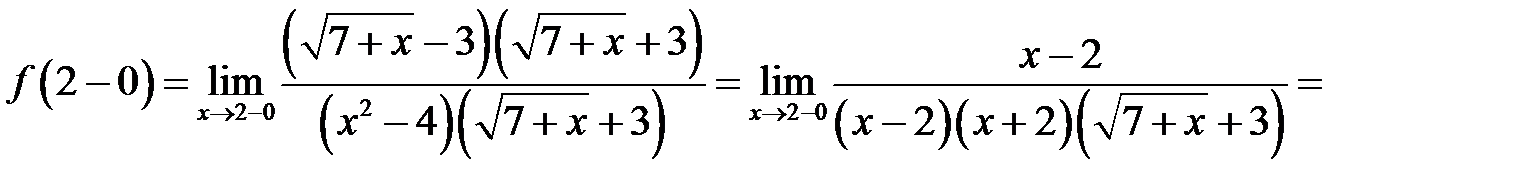
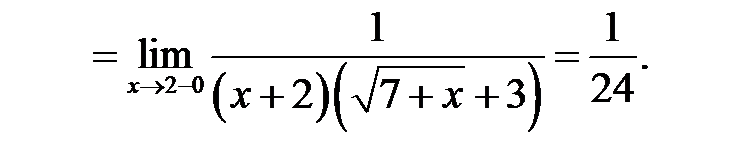
Аналогічно отримаємо

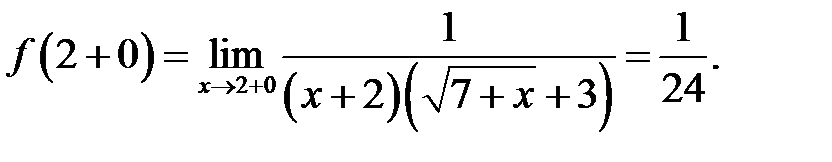
Отже, оскільки 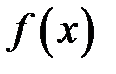не визначена в точці 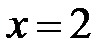, ця точка є точкою розриву першого роду (усувний розрив).

Приклад 4. Дослідити на неперервність функцію

Розв’язання. Область визначення функції

На області визначення функція неперервна, оскільки є елементарною. Функція 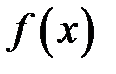визначена в проколених околах точок і 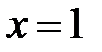і не визначена в самих цих точках, тому ці точки є точками розриву. Обчислимо

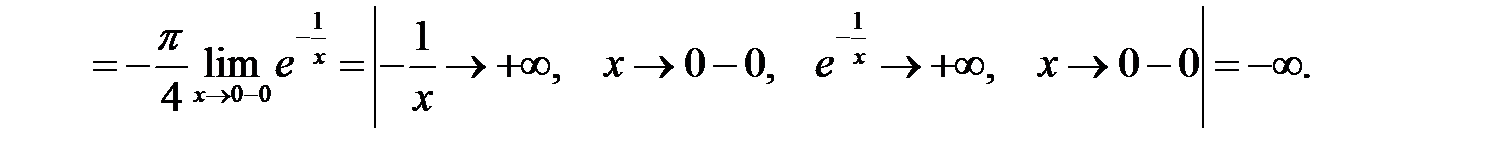
Аналогічно

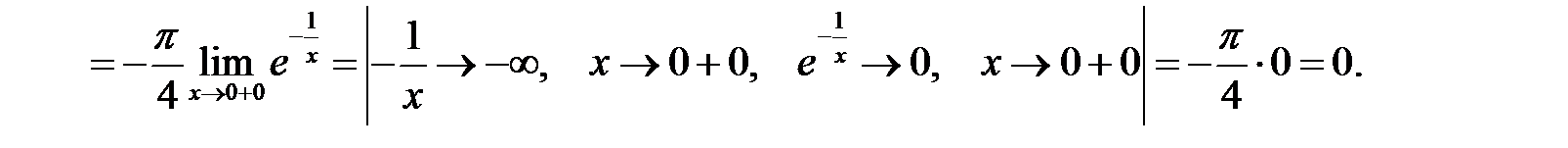
Таким чином, точка є точкою розриву другого роду.

Знайдемо

Аналогічно

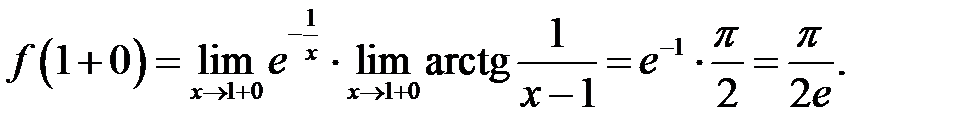
Таким чином, точка 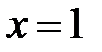є точкою розриву першого роду (не усувного). Величина стрибка функції 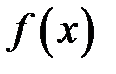в точці 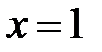дорівнює

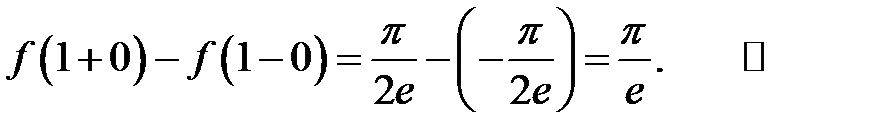
Приклад 5. Дослідити на рівномірну неперервність функцію 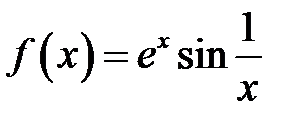на інтервалі .

Розв’язання. Рівномірна неперервність функції на множині означає, що малому приросту аргумента в довільній точці 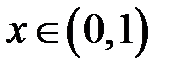відповідає малий приріст функції. Однак, для функції 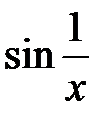це не так. Дійсно, достатньо взяти та 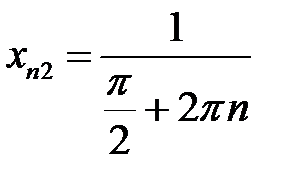. Тоді

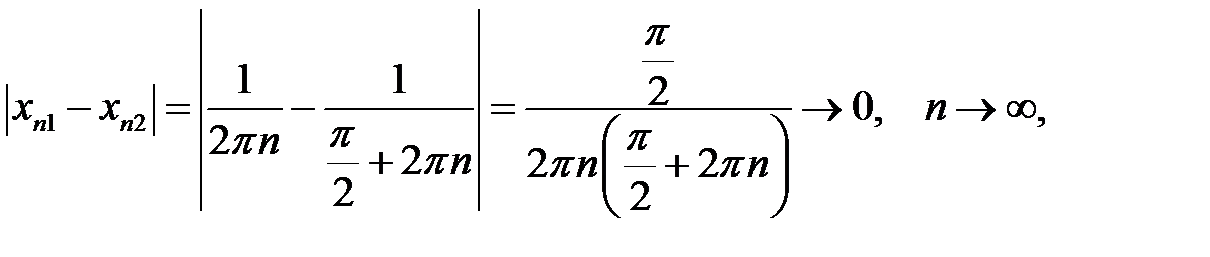
Але 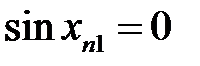, а 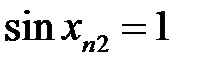. Отже, не слід очікувати рівномірної неперервності 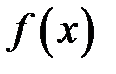на .

Доведемо строго, що 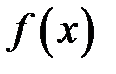не буде рівномірно неперервною на інтервалі . Побудуємо заперечення до означення рівномірної неперервності: існує 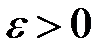таке, що для довільного 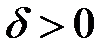можна вказати 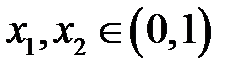такі, що 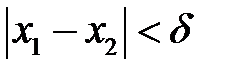, але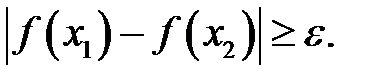

Візьмемо дві послідовності, вказані вище, а саме , , 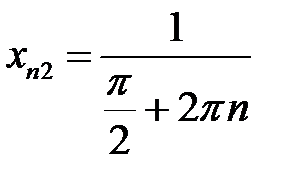. Ясно, що 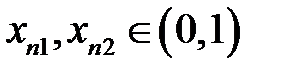. Оскільки

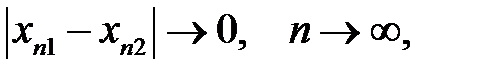
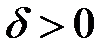то при достатньо великому для довільного . Але

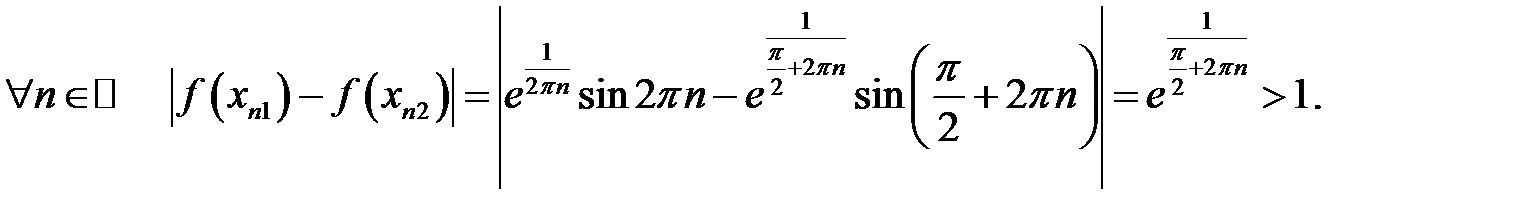
Отже, при 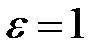умова рівномірної неперервності не виконується. Таким чином, 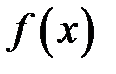не буду рівномірно неперервною на інтервалі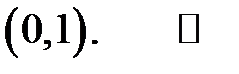

Завдання 1

Довести неперервність функції в точці 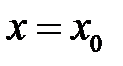за означенням:

1.

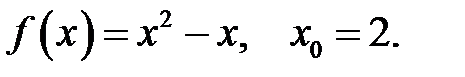
2.

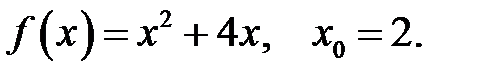
3.

4.

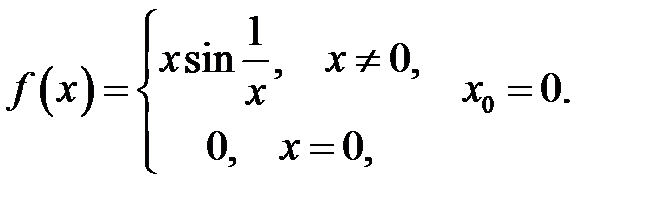
5.

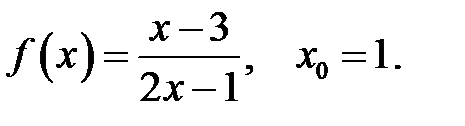
6.

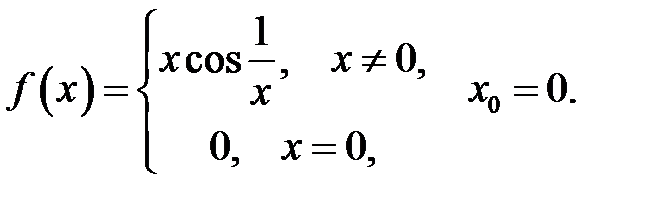
7.

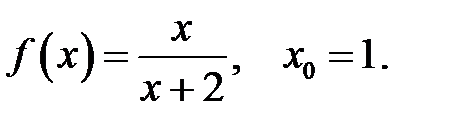
8.

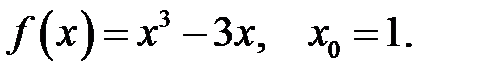
9.

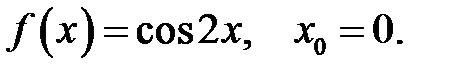
10.

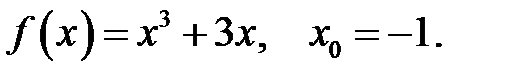
11.

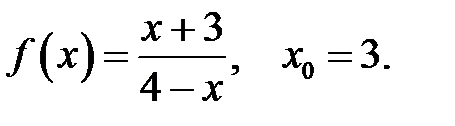
12.

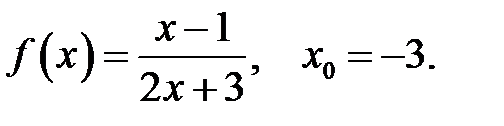
13.

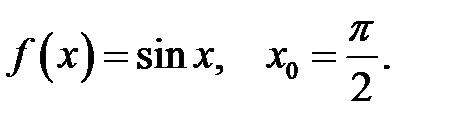
14.

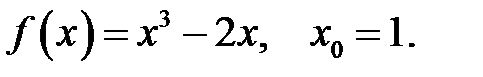
15.

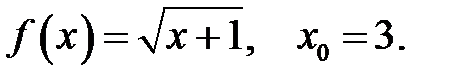
16.

17.

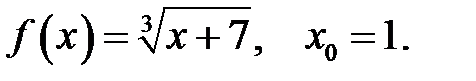
18.

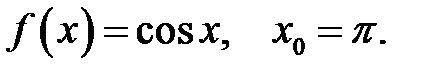
19.

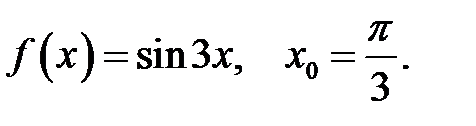
20.

21.

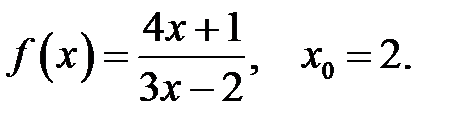
22.

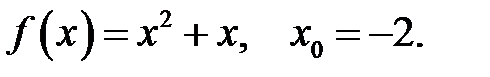
23.

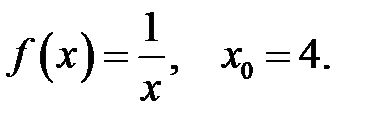
24.

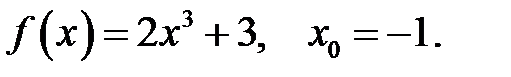
25.

26.

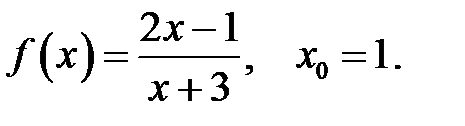
27.

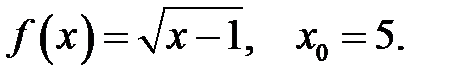
28.

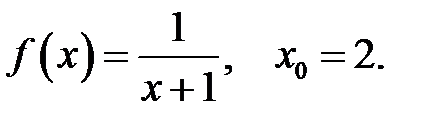
29.

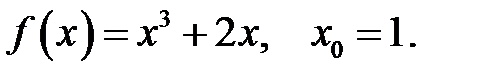
30.

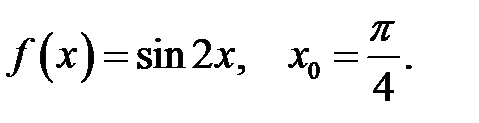
Завдання 2

Дослідити на неперервність і зобразити схематичні графіки функції в околі точок розриву:

1.

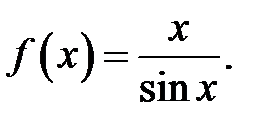
2.

3.

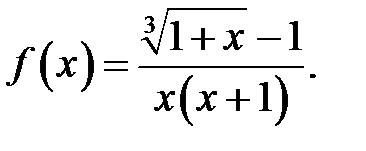
4.

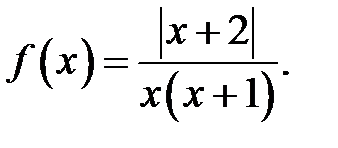
5.

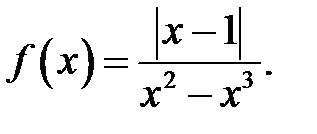
6.

7.

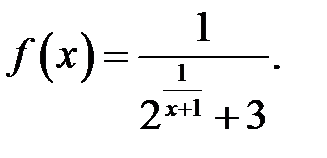
8. 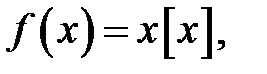де — ціла частина .

9.

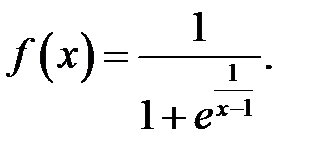
10.

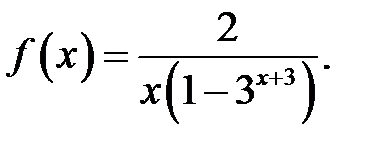
11.

12.

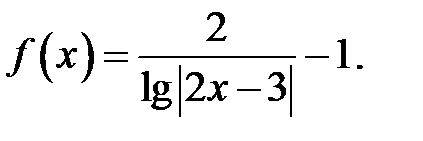
13.

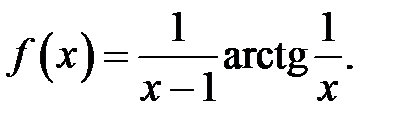
14.

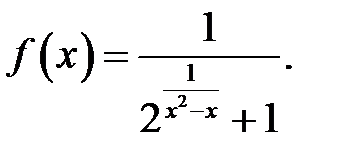
15.

16. 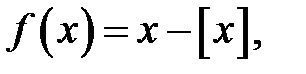де — ціла частина .

17.

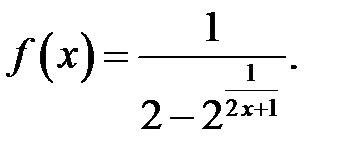
18.

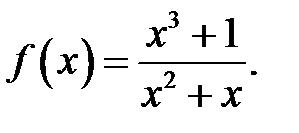
19.

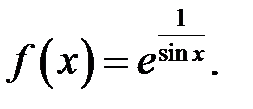
20.

21.

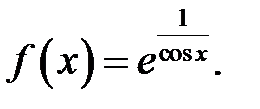
22.

23.

24. 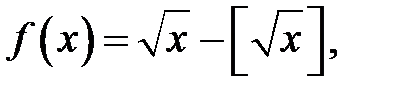де — ціла частина .

25.

26.

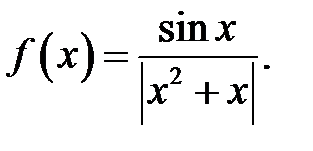
27.

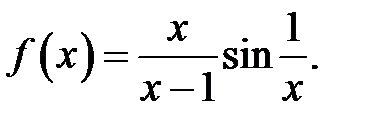
28. 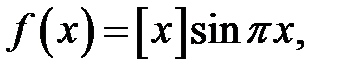де — ціла частина .

29.

30.

Завдання 3

Обчислити ліву і праву границі функції в точках її розриву та вказати тип точок розриву.

1.

2.

3.

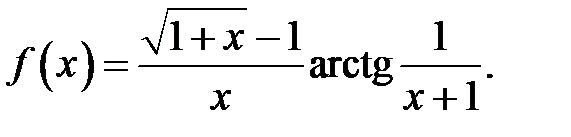
4.

5.

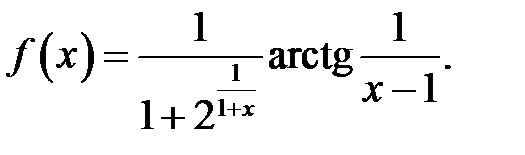
6.

7.

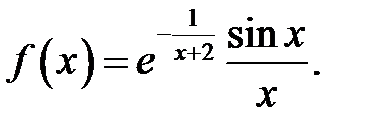
8.

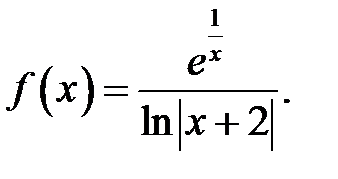
9.

10.

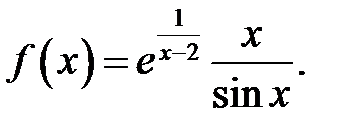
11.

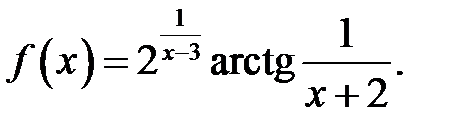
12.

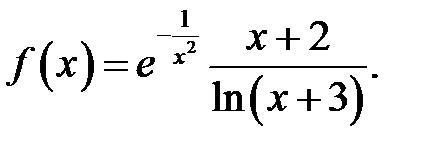
13.

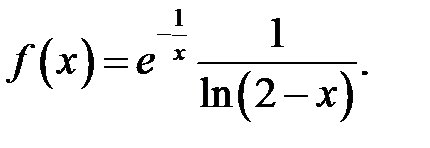
14.

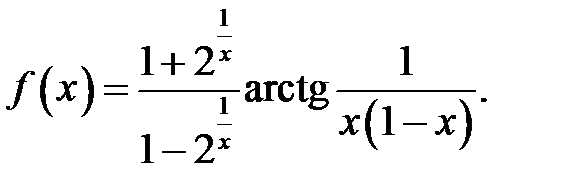
15.

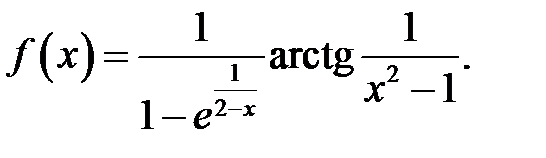
16.

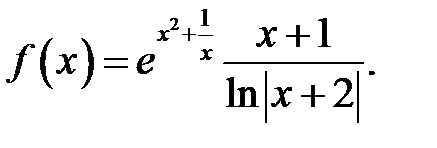
17.

18.

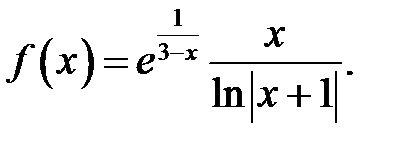
19.

20.

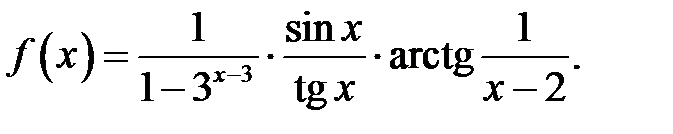
21.

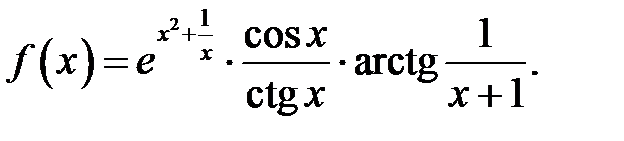
22.

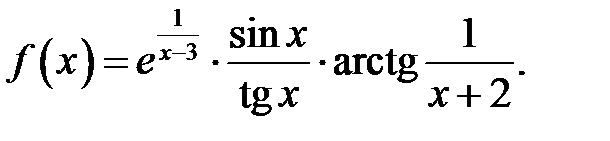
23.

24.

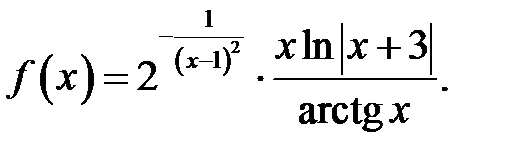
25.

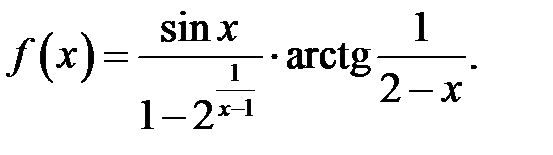
26.

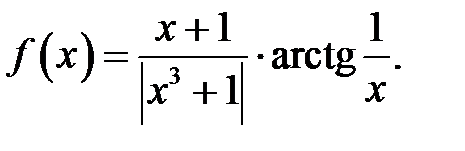
27.

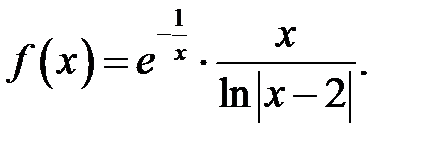
28.

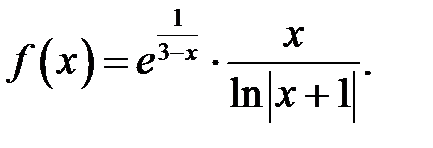
29.

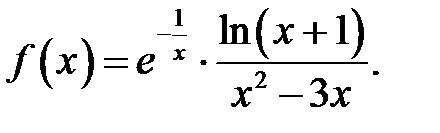
30.

Завдання 4

Довести, що рівняння має корінь .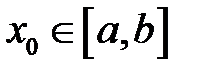

1.

2.

3.

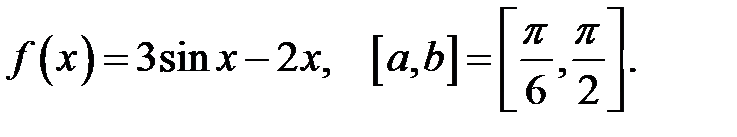
4.

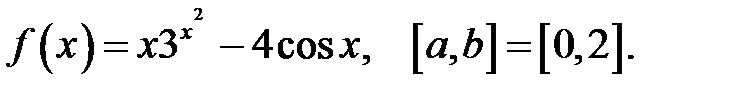
5.

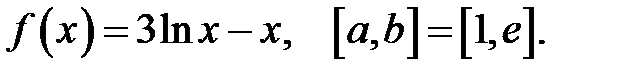
6.

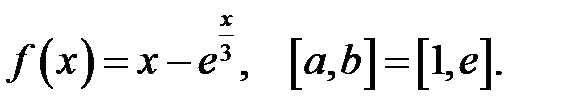
7.

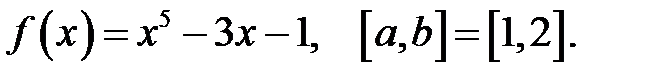
8.

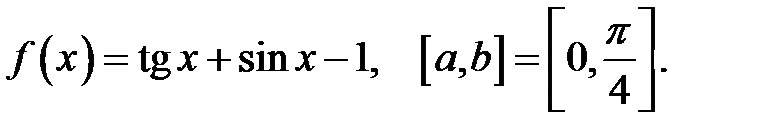
9.

10.

Довести, що крив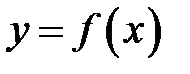і і 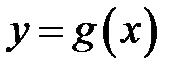мають спільну точку на відрізку .

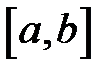11.

12.

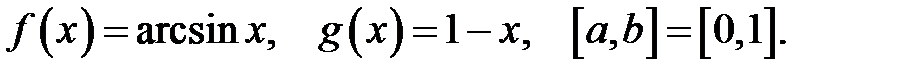
13.

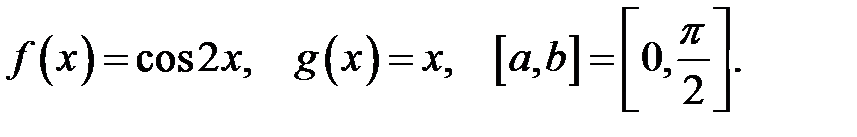
14.

15.

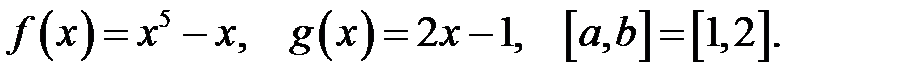
Знайти кількість усіх дійсних коренів наступних рівнянь.

16.

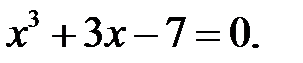
17.

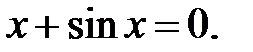
18.

19.

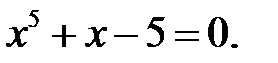
20.

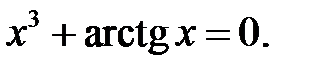
Дослідити на рівномірну непервність функції на заданих множинах (для 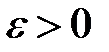знайти відповідне ).

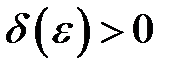21.

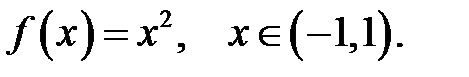
22.

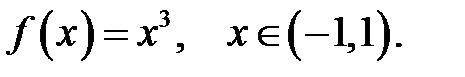
23.

24.

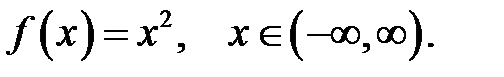
25.

26.

27.

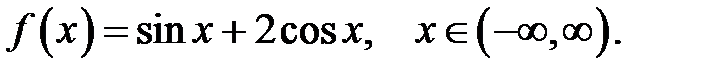
28.

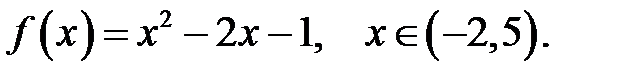
29.

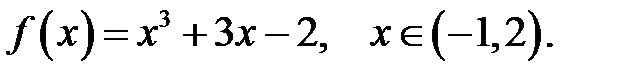
30.

Додаткові завдання

теоретичного характеру

1. Довести, що функція

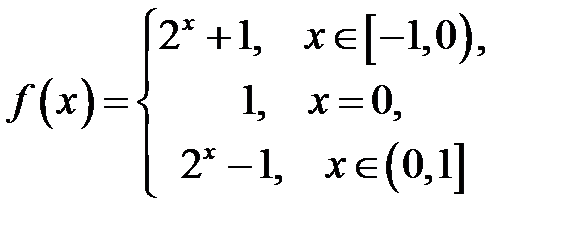
визначена та обмежена на відрізку 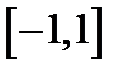, не має на ньому ні найбільшого, ні найменшого значення.

2. Довести, що функція Рімана

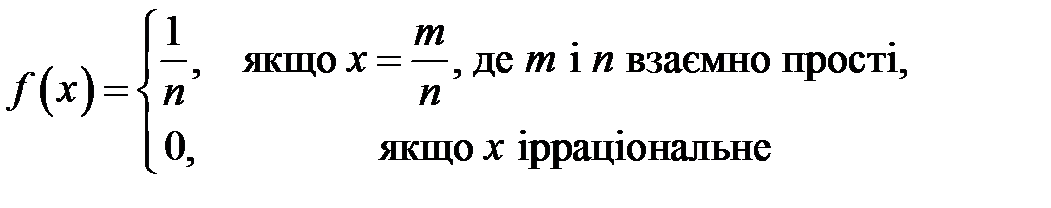
неперервна в кожній ірраціональній точці і розривна в кожній раціональній точці.

3. Довести, що функція Діріхле

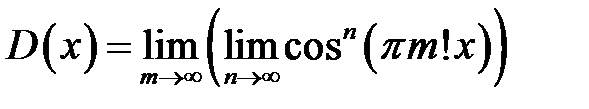
розривна при кожному дійсному значенні .

4. Знайти точки неперервності функції

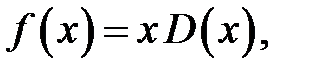
де 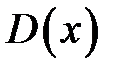— функція Діріхле (задача 3).

5. Дано, що 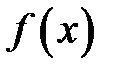неперервна, а має розрив у точці . Чи завжди буде розривною в точці сума ? Навести приклади.

6. Функці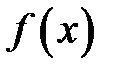ї і 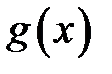мають розрив у точці . Чи завжди буде розривною в точці сума ? Навести приклади.

7. Чи можна стверджувати, що квадрат розривної функції є завжди розривна функція? Навести приклади.

8. Довести, що модуль неперервної функції є неперервною функцією.

9. Нехай функція 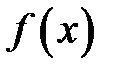неперервна на відрізку . Довести, що функція

теж неперервна на відрізку .

10. Нехай функція 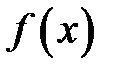неперервна на відрізку . Довести, що функція

теж неперервна на відрізку .

11. Чи можливо, щоб для немотонної функції , , 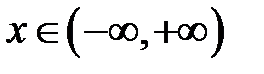існувала обернена? Розглянути приклад

12. Довести, що функція

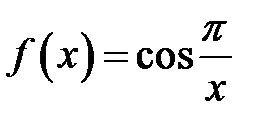
неперервна і обмежена на інтервалі , але не є рівномірно неперервною на ньому.

13. Довести, що функція

неперервна і обмежена на інтервалі , але не є рівномірно неперервною на ньому.

14. Дослідити на рівномірну неперервність функцію

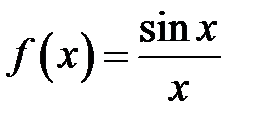
на інтервалі .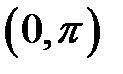

15. Дослідити на рівномірну неперервність функцію

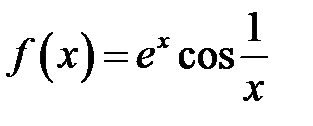
на інтервалі .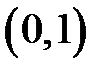

16. Числова множина називається відкритою, якщо кожна точка із має окіл, що входить в .

Довести, що кожний інтервал є відкритою множиною.

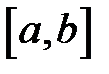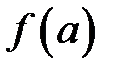17. Нехай функція неперервна на відрізку , і число знаходиться між та 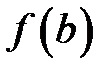. Довести, що множина

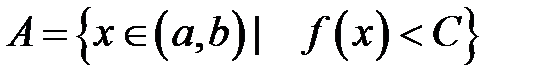
є відкритою.

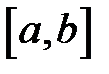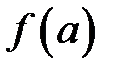18. Нехай функція неперервна на відрізку , і число знаходиться між та 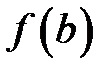. Довести, що множина

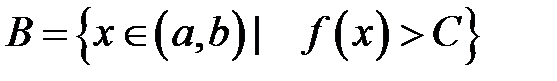
є відкритою.

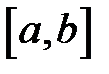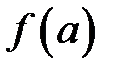19. Нехай функція неперервна на відрізку , і число знаходиться між та 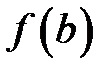. Довести, що множина

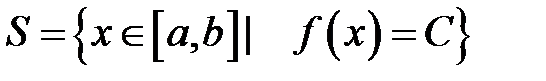
має найбільший та найменший елементи.

20. Числова множина 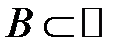називається замкнутою, якщо її доповнення 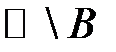— відкрита множина (задача 16).

Нехай функція неперервна при всіх 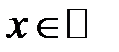, множина ,

—

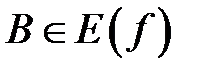прообраз множини 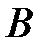. Довести, що якщо 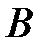— замкнута множини, то її прообраз 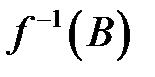теж є замкнутою множиною.

21. Нехай функція неперервна при всіх 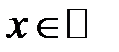, множина ,

—

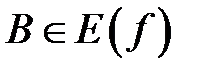прообраз множини 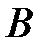. Довести, що якщо 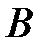— відкрита множини, то її прообраз 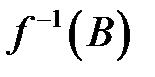теж є відкритою множиною.

22. Довести критерій неперервності функції 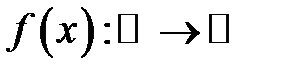. Для того, щоб функція 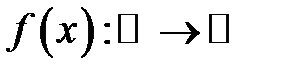була неперервною на , необхідно і достатньо, щоб прообраз кожної відкритої множини в був відкритою множиною.

23. Чи існує неперервне відображення

a. відрізка на інтервал;

b. інтервала на відрізок?

побудувати взаємно однозначне відображення відрізка на інтервал.

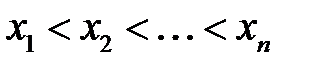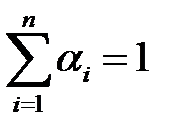24. Функція неперервна на інтервалі . Довести, що для довільних чисел із інтервала і довільних чисел , існує число 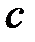, , 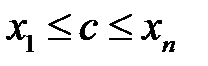таке, що

.

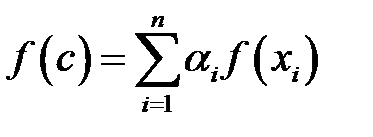25. 1) Довести, що існує нескінченно багато функцій 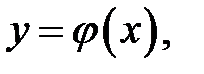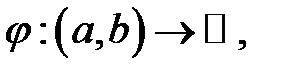які задовольняють рівняння

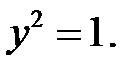
2) Нехай 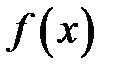— неперервна і додатна на інтервалі функція. Довести, що існує єдина неперервна на функція 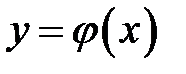, що задовольняє рівняння

і умову 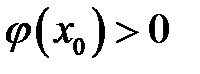для деякої точки .

26. Знайти всі неперервні на числовій прямій функції такі, що для довільного справедлива рівність

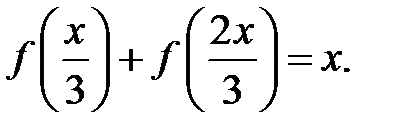
27. Знайти всі неперервні на числовій прямій функції такі, що для довільного справедлива рівність

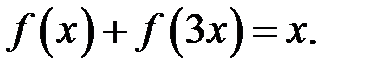
28. Знайти всі неперервні на числовій прямій функції такі, що для довільного справедлива рівність

29. Знайти всі неперервні на числовій прямій функції такі, що для довільних задовольняють рівність

30. Знайти всі неперервні на числовій прямій функції такі, що для довільних задовольняють рівність

Читайте також:

1. Адвокатура в Україні: основні завдання і функції
2. Алгоритм знаходження ДДНФ (ДКНФ) для даної булевої функції
3. Але відмінні від значення функції в точці або значення не існує, то точка називається точкою усувного розриву функції .
4. Аналіз коефіцієнтів цільової функції
5. АРХІВНІ ДОВІДНИКИ В СИСТЕМІ НДА: ФУНКЦІЇ ТА СТРУКТУРА
6. АРХІВНІ ДОВІДНИКИ В СИСТЕМІ НДА: ФУНКЦІЇ ТА СТРУКТУРА
7. Асимптоти графіка функції
8. Асимптоти графіка функції
9. Базальні ядра, їх функції, симптоми ураження
10. Базові функції, логічні функції
11. Банки як провідні суб’єкти фінансового посередництва. Функції банків.
12. Банківська система та її основні функції

Переглядів: 5389