
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Границя функції
Дійсне число 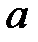 називається граничною точкою множини
називається граничною точкою множини 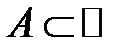 , якщо
, якщо
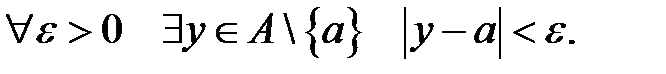
Кажуть, що 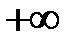 є граничною точкою множини
є граничною точкою множини 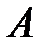 , якщо
, якщо
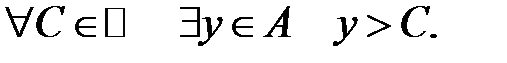
Кажуть, що 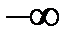 є граничною точкою множини
є граничною точкою множини 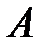 , якщо
, якщо
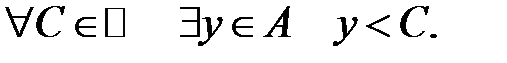
Нехай 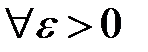 , а
, а 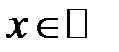 . Інтервал
. Інтервал 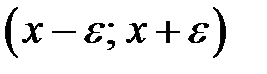 називається
називається 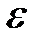 -околом точки
-околом точки 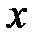 і позначається
і позначається 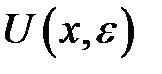 . Множина
. Множина
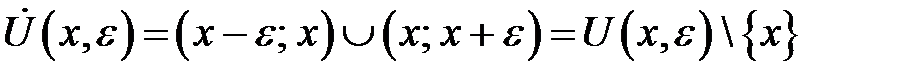
називається проколеним 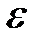 -околом точки
-околом точки 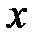 .
.
Надалі будемо припускати, що точка 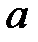 є граничною точкою області визначення
є граничною точкою області визначення 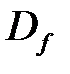 функції
функції 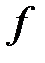 .
.
Означення (Коші). Число 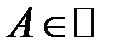 називають границею функції
називають границею функції 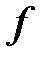 в точці
в точці 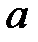 , якщо
, якщо
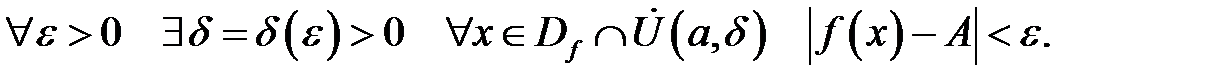
Означення (Гейне). Число 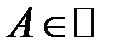 називають границею функції
називають границею функції 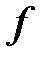 в точці
в точці 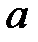 , якщо для довільної послідовності
, якщо для довільної послідовності 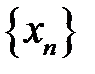 , що задовольняє умовам
, що задовольняє умовам
1. 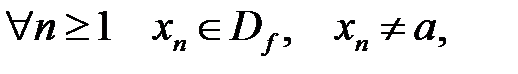
2. 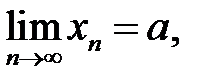
виконується співвідношення
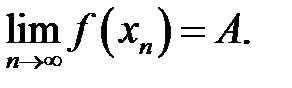
Позначення:  або
або 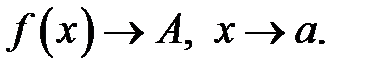
Ці означення рівносильні. Означенням границі функції за Гейне зручно користуватись у тому випадку, коли потрібно довести, що функція не має границі в точці. Для цього досить довести, що існують дві послідовності 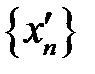 та
та 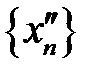 , які задовольняють умовам означення, але відповідні послідовності значень функції
, які задовольняють умовам означення, але відповідні послідовності значень функції 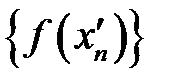 та
та 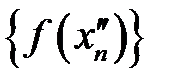 не мають однакових границь.
не мають однакових границь.
Кажуть, що
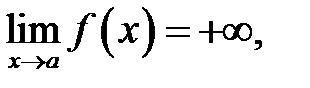
якщо
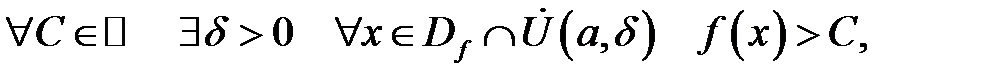
та
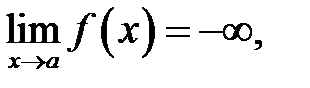
якщо
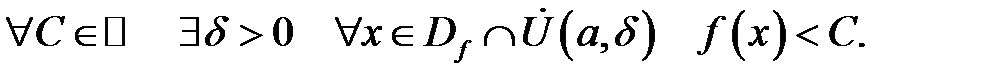
Число 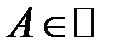 називають границею функції
називають границею функції 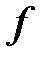 при
при 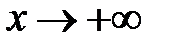 , якщо
, якщо
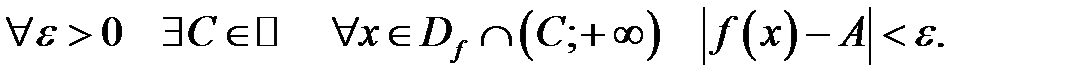
Позначення: 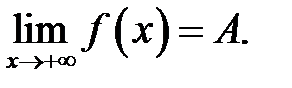
Число 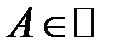 називають границею функції
називають границею функції 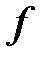 при
при 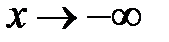 , якщо
, якщо
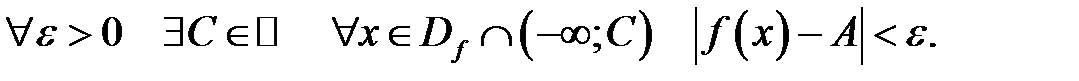
Позначення: 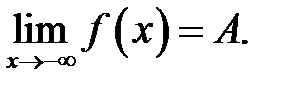
Всі властивості границь послідовностей легко переносяться на границі функцій в точці.
Запишемо дві важливі границі, які часто використовують при обчисленні інших границь функцій:
I. 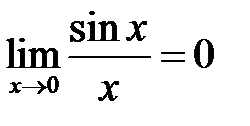 — перша визначна (важлива) границя;
— перша визначна (важлива) границя;
II. 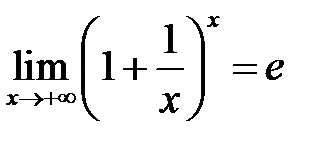 — друга визначна (важлива) границя.
— друга визначна (важлива) границя.
Введемо поняття односторонніх границь.
Число 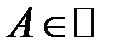 називають границею справа функції
називають границею справа функції 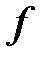 в точці
в точці 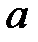 , якщо
, якщо
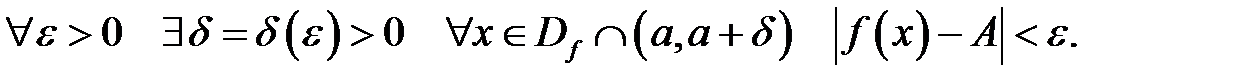
Позначення: 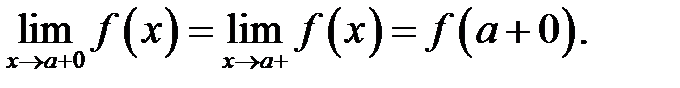
Число 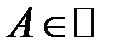 називають границею зліва функції
називають границею зліва функції 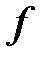 в точці
в точці 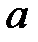 , якщо
, якщо
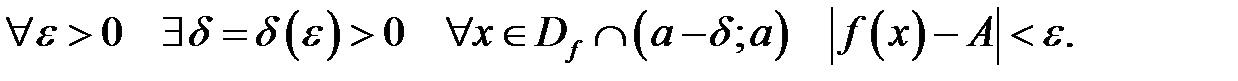
Позначення: 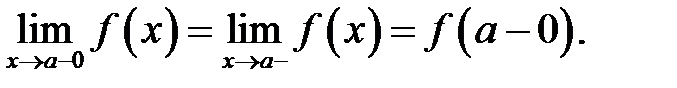
Для того, щоб  , необхідно і достатньо, щоб
, необхідно і достатньо, щоб
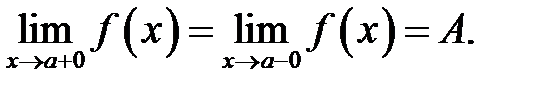
Функція 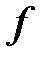 називається нескінченно малою (НМ) при
називається нескінченно малою (НМ) при  (або в точці
(або в точці 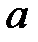 ), якщо
), якщо

Функція 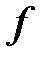 називається нескінченно великою (НВ) при
називається нескінченно великою (НВ) при  (або в точці
(або в точці 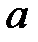 ), якщо
), якщо
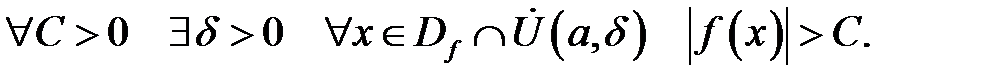
Властивості нескінченно малих функцій:
1. Сума скінченного числа нескінченно малих є нескінченно малою.
2. Добуток скінченного числа нескінченно малих є нескінченно малою.
3. Добуток нескінченно малої функції та обмеженої функції є нескінченно малою.
4. Якщо функція 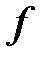 є нескінченно малою при
є нескінченно малою при  , але відмінна від нуля в околі точки
, але відмінна від нуля в околі точки 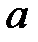 , то
, то 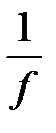 є нескінченно великою в цій точці.
є нескінченно великою в цій точці.
Для того, щоб  , необхідно і достатньо, щоб мало місце представлення
, необхідно і достатньо, щоб мало місце представлення
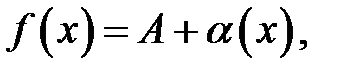
де 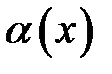 — нескінченно мала функція при
— нескінченно мала функція при  .
.
Якщо 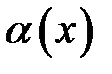 і
і 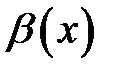 є нескінченно малими при
є нескінченно малими при  , то при
, то при
1. 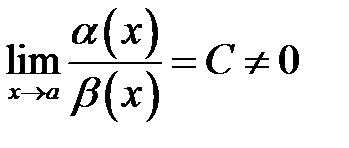 вони називаються нескінченно малими одного порядку малості при
вони називаються нескінченно малими одного порядку малості при  ;
;
2. 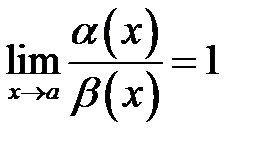 вони називаються еквівалентними нескінченно малими при
вони називаються еквівалентними нескінченно малими при  ;
;
3. 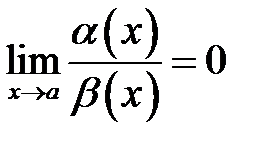 функція
функція 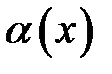 називається нескінченно малою вищого порядку малості при
називається нескінченно малою вищого порядку малості при  ніж
ніж 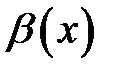 , що позначають
, що позначають 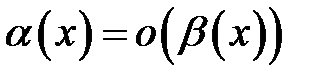 (
( 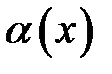 дорівнює «о мале» від
дорівнює «о мале» від 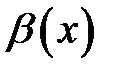 при
при  );
);
4. 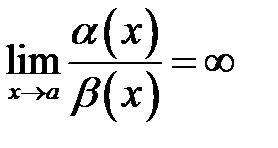 функція
функція 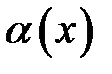 називається нескінченно малою нижчого порядку малості при
називається нескінченно малою нижчого порядку малості при  ніж
ніж 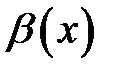 , що позначають
, що позначають 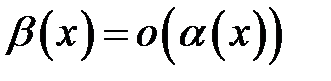 при
при  ;
;
5. 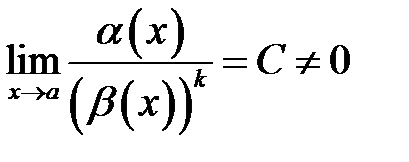 функція
функція 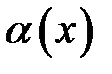 має порядок малості
має порядок малості 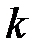 відносно
відносно 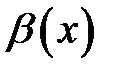 при
при  ;
;
6. якщо 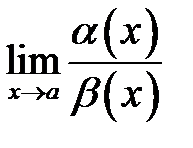 не існує, то нескінченно малі
не існує, то нескінченно малі 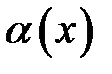 і
і 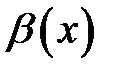 називаються непорівнюваними при
називаються непорівнюваними при  .
.
Якщо 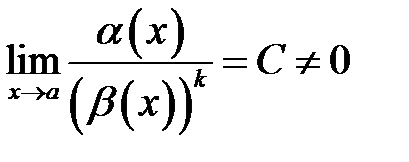 , то функція
, то функція 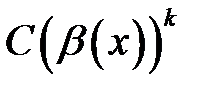 називається головною частиною нескінченно малої
називається головною частиною нескінченно малої 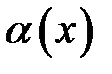 відносно
відносно 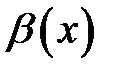 при
при  .
.
Якщо 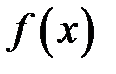 і
і 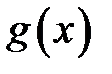 є нескінченно великими при
є нескінченно великими при  , то при
, то при
1. 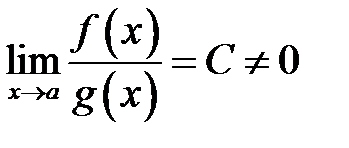 вони називаються нескінченно великими одного порядку росту при
вони називаються нескінченно великими одного порядку росту при  ;
;
2. 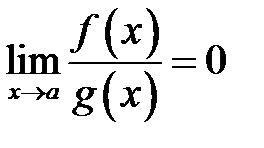 функція
функція 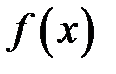 називається нескінченно великою нижчого порядку росту при
називається нескінченно великою нижчого порядку росту при  ніж
ніж 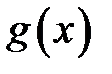 ;
;
3. 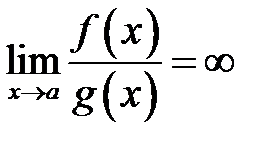 функція
функція 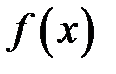 називається нескінченно великою вищого порядку росту при
називається нескінченно великою вищого порядку росту при  ніж
ніж 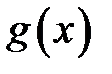 ;
;
4.  функція
функція 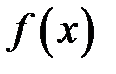 має порядок ростуі
має порядок ростуі 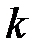 відносно
відносно 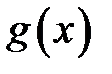 при
при  ;
;
5. якщо 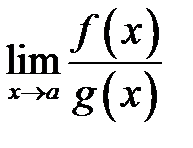 не існує, то нескінченно великі
не існує, то нескінченно великі 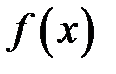 і
і 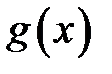 називаються непорівнюваними при
називаються непорівнюваними при  .
.
Якщо 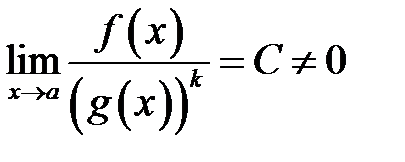 , то функція
, то функція 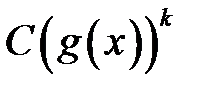 називається головною частиною нескінченно великої
називається головною частиною нескінченно великої 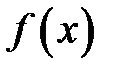 відносно
відносно 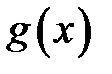 при
при  .
.
Для того, щоб нескінченно малі 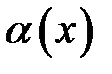 і
і 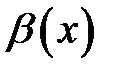 були еквівалентними при
були еквівалентними при  , необхідно і достатньо, щоб
, необхідно і достатньо, щоб 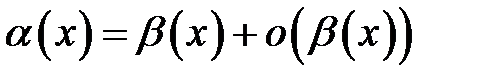 при
при  .
.
Границя добутку (відношення) функцій не змінюється, якщо в ньому замінити нескінченно малу на еквівалентну нескінченно малу функцію.
Таблиця еквівалентних нескінченно малих:
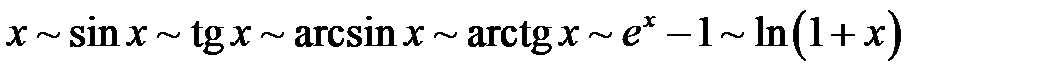 при
при 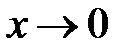 ;
;
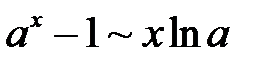 при
при 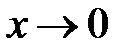 ;
;
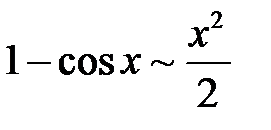 при
при 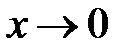 ;
;
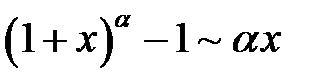 при
при 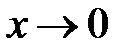 .
.
Приклад 1. Довести за означенням, що границя
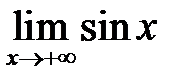
не існує.
Доведення. Доведемо, що ця функція не задовольняє означенню границі функції за Гейне при 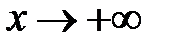 . Для цього розглянемо послідовності
. Для цього розглянемо послідовності 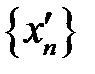 та
та 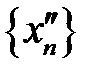 , де
, де
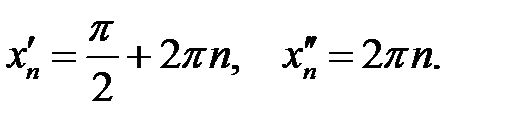
Тоді
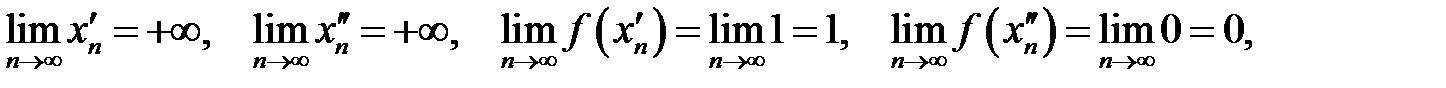
А оскільки 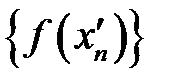 та
та 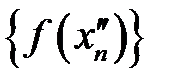 мають різні границі, то границя
мають різні границі, то границя
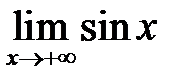
не існує. 
Приклад 2. Довести за означенням, що границя
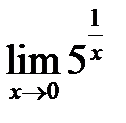
не існує.
Доведення. Розглянемо послідовності 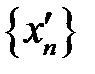 та
та 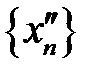 , де
, де
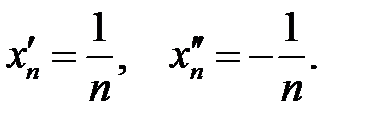
Тоді
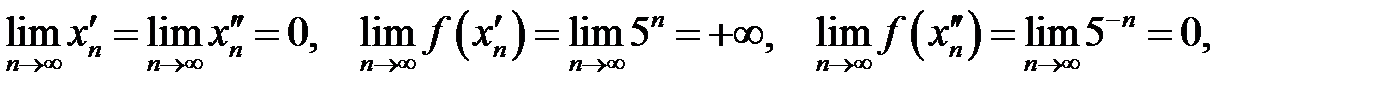
А оскільки 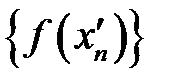 та
та 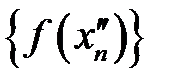 мають різні границі, то границя
мають різні границі, то границя
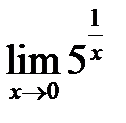
не існує. 
У найпростіших випадках обчислення границі  зводиться до підстановки у функцію
зводиться до підстановки у функцію 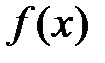 граничного значення аргумента, наприклад,
граничного значення аргумента, наприклад,
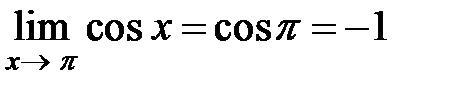 .
.
Проте часто така підстановка приводить до невизначених виразів, зокрема, таких:
1) невизначеність типу 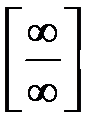 (відношення двох нескінченно великих величин);
(відношення двох нескінченно великих величин);
2) невизначеність типу 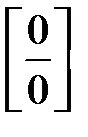 (відношення двох нескінченно малих величин);
(відношення двох нескінченно малих величин);
3) невизначеність типу 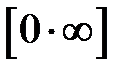 (добуток нескінченно малої величини на нескінченно велику);
(добуток нескінченно малої величини на нескінченно велику);
4) невизначеність типу 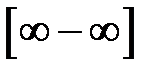 (різниця двох нескінченно великих величин);
(різниця двох нескінченно великих величин);
5) невизначеності типу 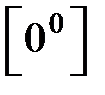 ,
, 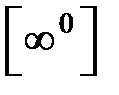 ,
, 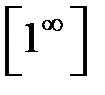 .
.
Операцію обчислення границі у цих випадках називають розкриттям невизначеності. Розглянемо деякі способи розкриття невизначеності.
1. Невизначеність типу 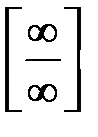 задана відношенням двох многочленів.Такі невизначеності можна розкривати за правилом:
задана відношенням двох многочленів.Такі невизначеності можна розкривати за правилом:
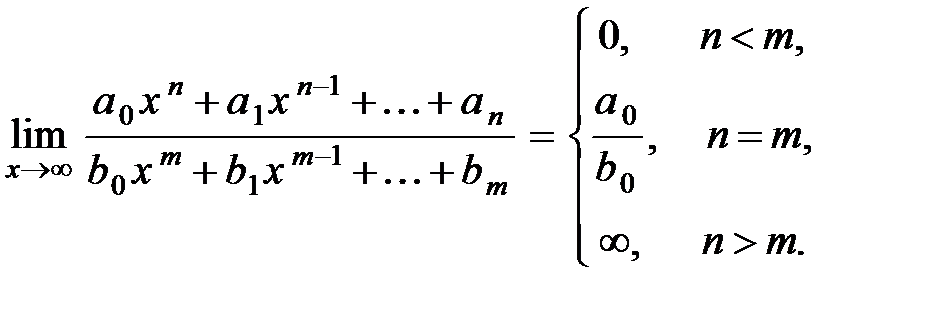
Приклад 3.Обчислити границі:
а) 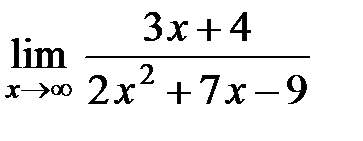 ; ;
| б) 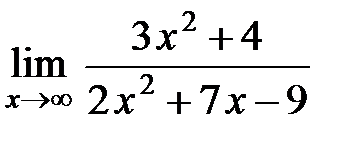 ; ;
| в) 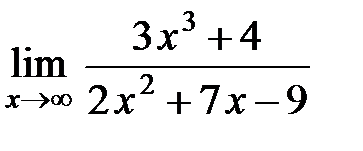 . .
|
Розв’язання. Користуючись наведеним вище правилом, легко знаходимо:
а) 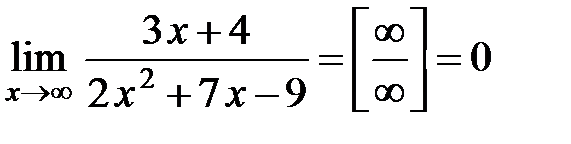 ;
;
б) 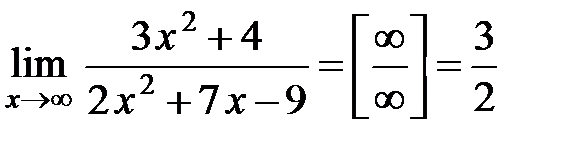 ;
;
в) 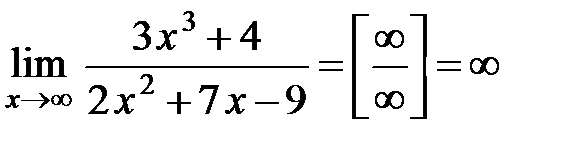 .
.
Відповідь:а) 0; б) 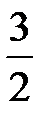 ; в)
; в)  .
.
2. Невизначеність типу 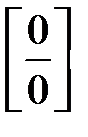 задана відношенням двох многочленів.
задана відношенням двох многочленів.
Приклад 4. Обчислити границю 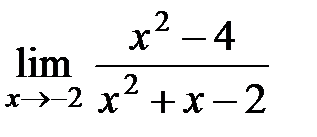 .
.
Розв’язання. Оскільки
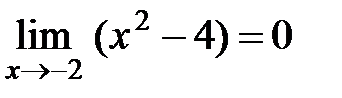 ,
, 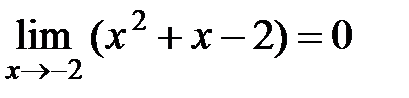 ,
,
то маємо невизначеність типуу 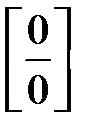 . Щоб її розкрити, розкладемо чисельник і знаменник на множники:
. Щоб її розкрити, розкладемо чисельник і знаменник на множники:
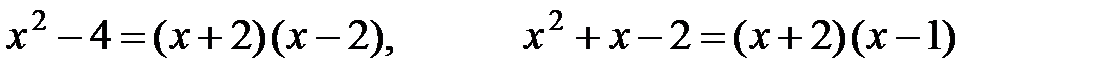 .
.
Скорочуючи на 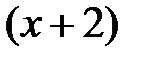 , маємо:
, маємо:
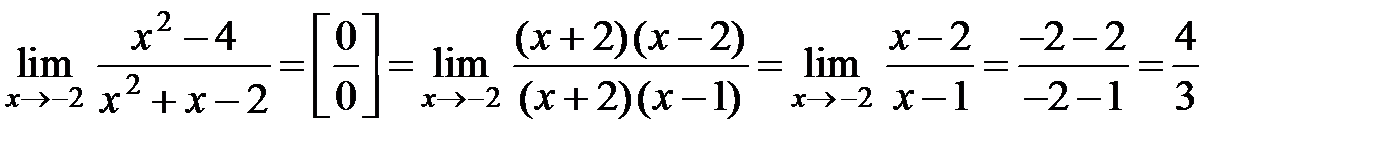 .
.
Відповідь: 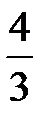 .
. 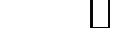
Множник 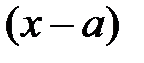 , через який чисельник і знаменник прямують до нуля, називають критичним множником. Отже, щоб розкрити невизначеність виду
, через який чисельник і знаменник прямують до нуля, називають критичним множником. Отже, щоб розкрити невизначеність виду 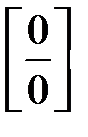 , задану відношенням двох многочленів, треба скоротити дріб на критичний множник.
, задану відношенням двох многочленів, треба скоротити дріб на критичний множник.
3. Невизначеність типу 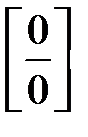 задана ірраціональними виразами.
задана ірраціональними виразами.
Приклад 5. Обчислити границю 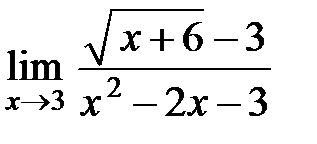 .
.
Розв’язання. Для обчислення границі помножимо й поділимо дріб на вираз, спряжений з чисельником, а потім розкладемо на множники знаменник і чисельник і скоротимо на критичний множник:
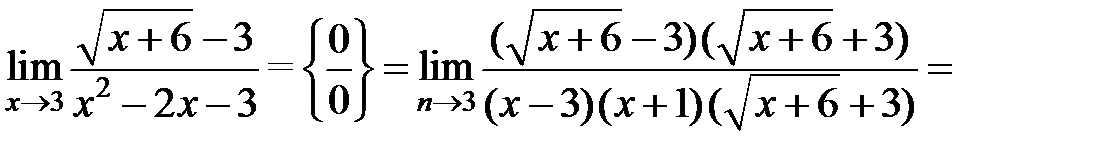
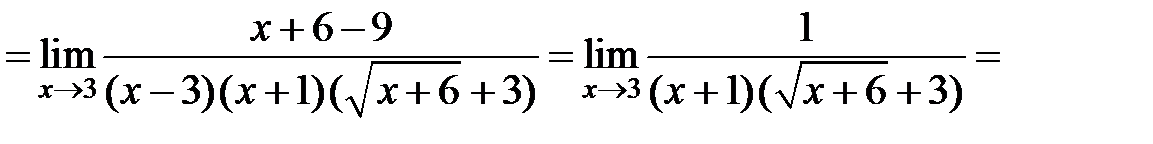
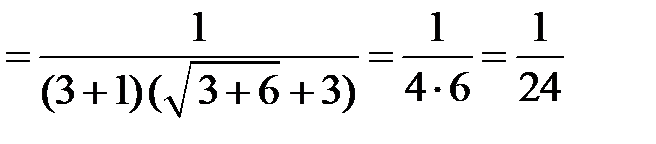 .
.
Відповідь: 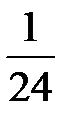 .
. 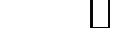
У випадку, коли корені кубічні, вираз доповнюють не до різниці квадратів, а до різниці кубів.
4. Невизначеність задана трансцендентними виразами.
У випадку, коли невизначеність задана тригонометричними виразами тощо, користуються еквівалентністю нескінченно малих функцій.
Приклад 6. Обчислити границю
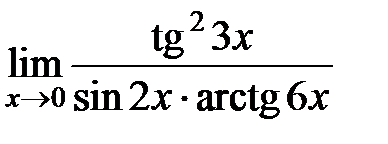 .
.
Розв’язання. При 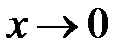
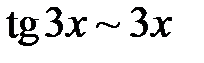 ,
, 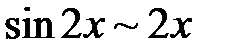 ,
, 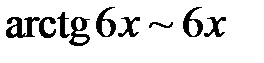 . Замінюючи нескінченно малі величини еквівалентними їм величинами, дістанемо:
. Замінюючи нескінченно малі величини еквівалентними їм величинами, дістанемо:
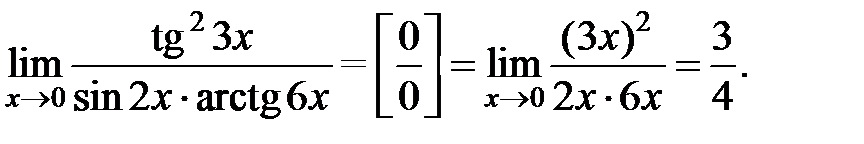
Відповідь: 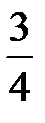 .
. 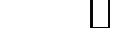
Якщо границю потрібно обчислити не в точці 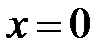 , то часто використовують заміни.
, то часто використовують заміни.
Приклад 7. Обчислити границю
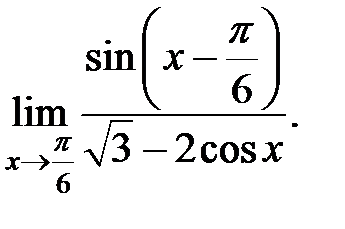 .
.
Розв’язання. Маємо невизначеність типу 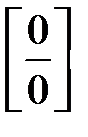 . Зробимо заміну
. Зробимо заміну 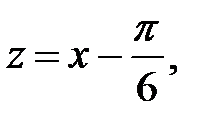 тоді при
тоді при 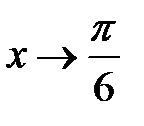
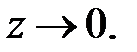
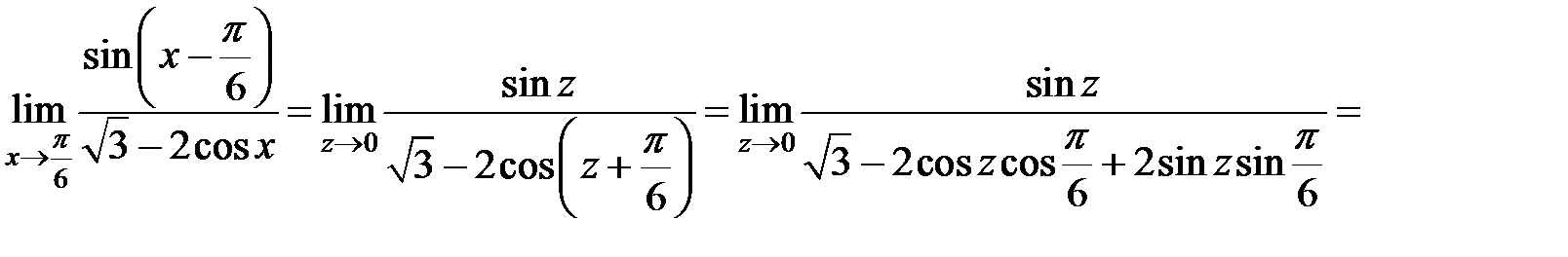
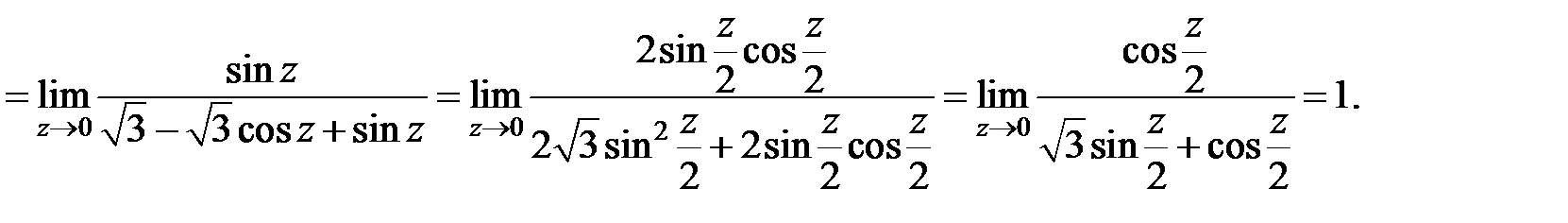
Відповідь: 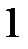 .
. 
5. Невизначеність типу 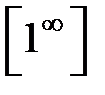 .
.
ЇЇ розкривають за допомогою другої визначної границі.
Приклад 8. Обчислити границю
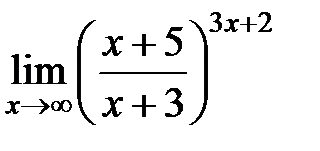 .
.
Розв’язання. Використовуючи другу визначну границю, дістанемо:
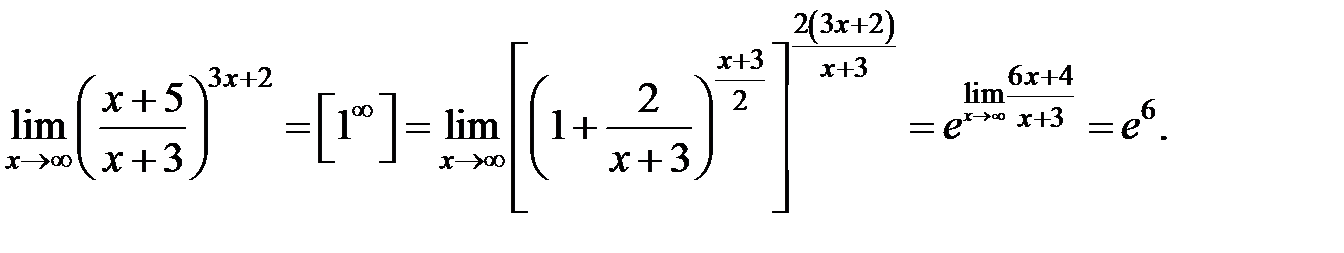
Відповідь: 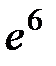 .
. 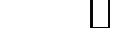
Завдання 1
Довести за означенням, що границя не існує:
1. 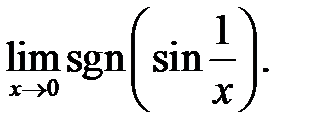
2. 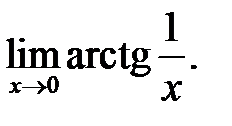
3. 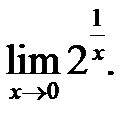
4. 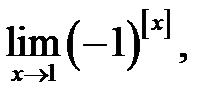 де
де  — ціла частина
— ціла частина  .
.
5. 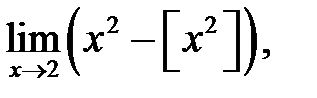 де
де  — ціла частина
— ціла частина  .
.
6. 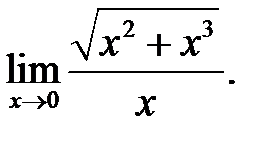
7. 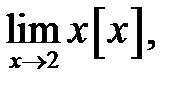 де
де  — ціла частина
— ціла частина  .
.
8. 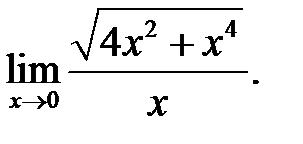
9. 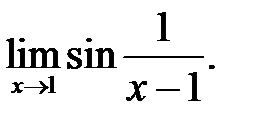
10. 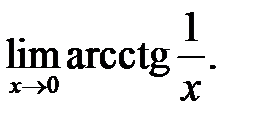
11. 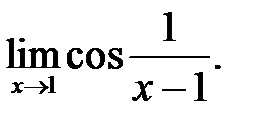
12. 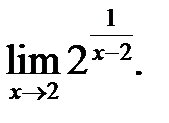
13. 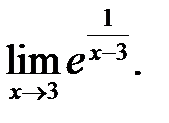
14. 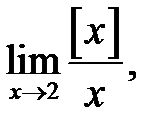 де
де  — ціла частина
— ціла частина  .
.
15. 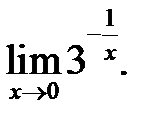
16. 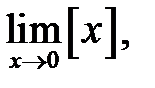 де
де  — ціла частина
— ціла частина  .
.
17. 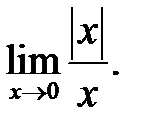
18. 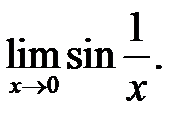
19. 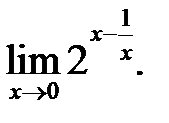
20. 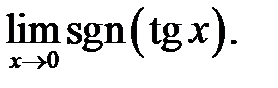
21. 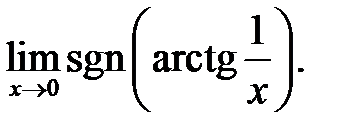
22. 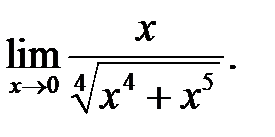
23. 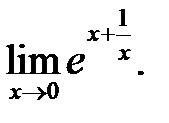
24. 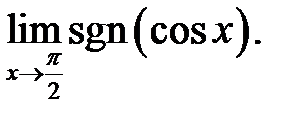
25. 
26. 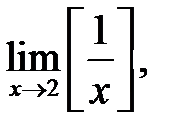 де
де  — ціла частина
— ціла частина  .
.
27. 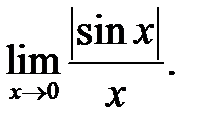
28. 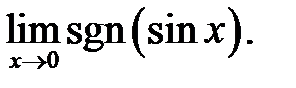
29. 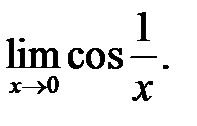
30. 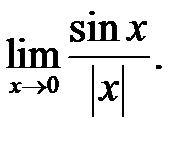
Завдання 2
Обчислити границі:
1. 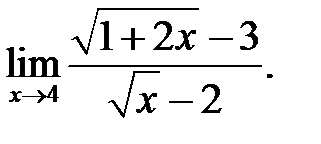
2. 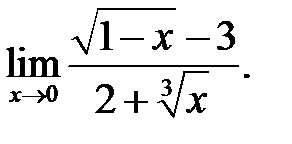
3. 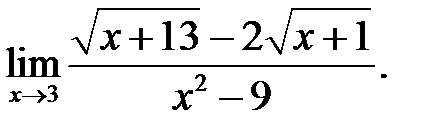
4. 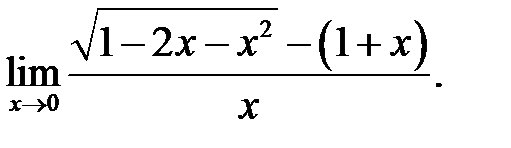
5. 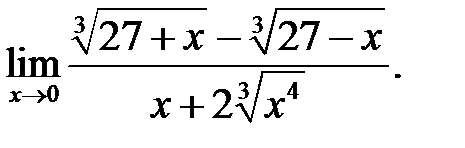
6. 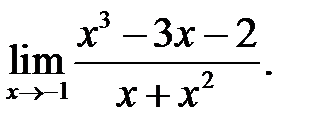
7. 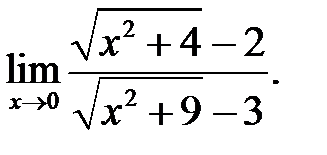
8. 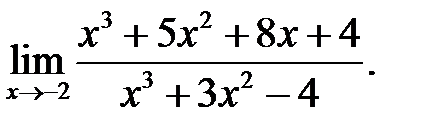
9. 
10. 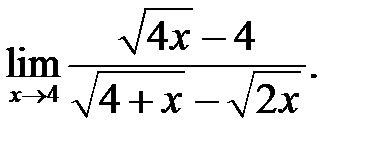
11. 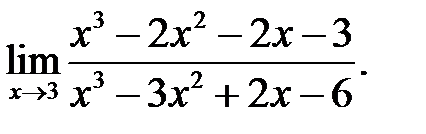
12. 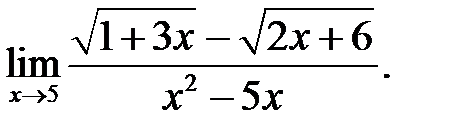
13. 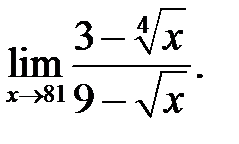
14. 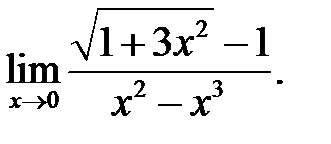
15. 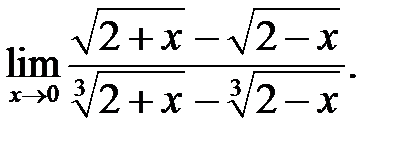
16. 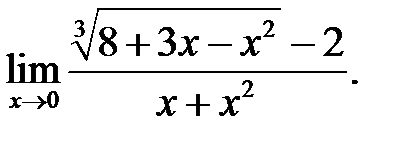
17. 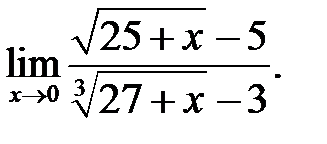
18. 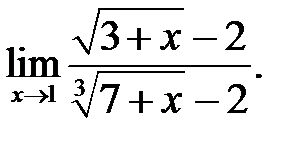
19. 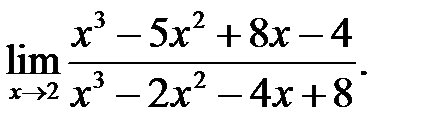
20. 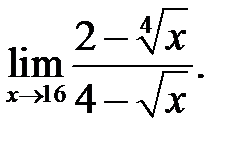
21. 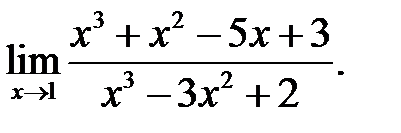
22. 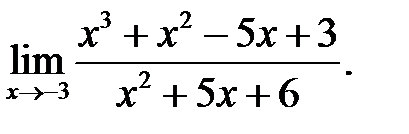
23. 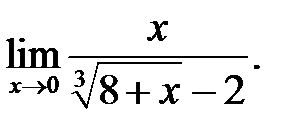
24. 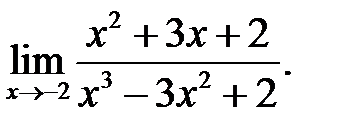
25. 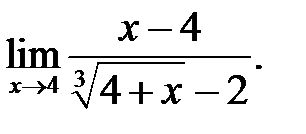
26. 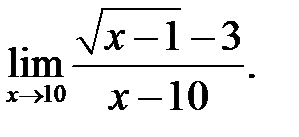
27. 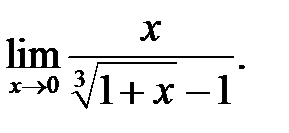
28. 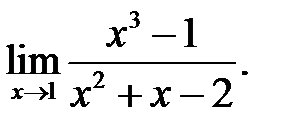
29. 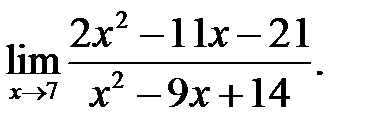
30. 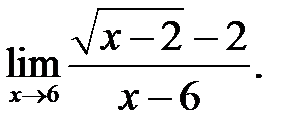
Завдання 3
Обчислити границі:
1. 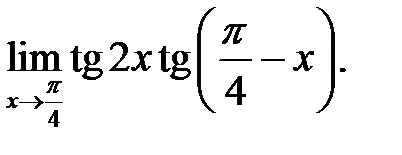
2. 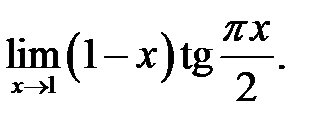
3. 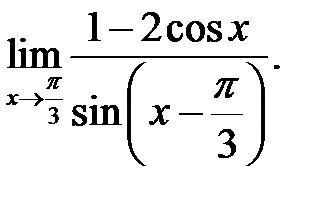
4. 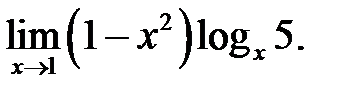
5. 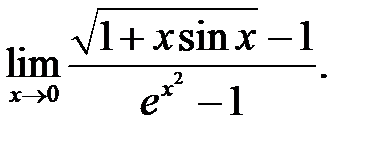
6. 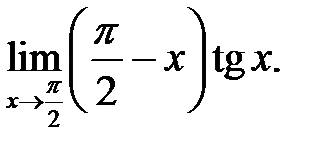
7. 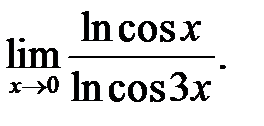
8. 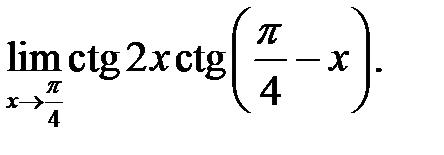
9. 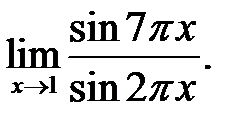
10. 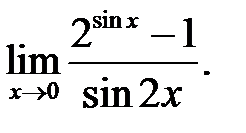
11. 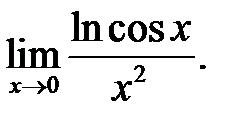
12. 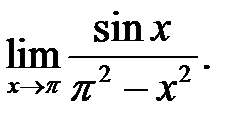
13. 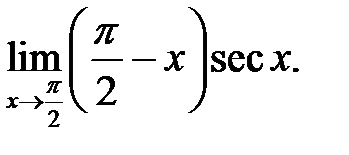
14. 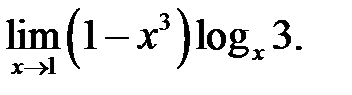
15. 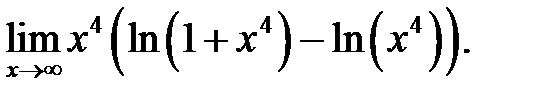
16. 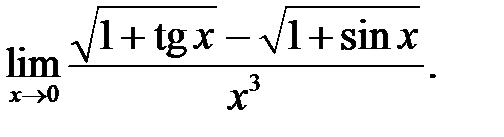
17. 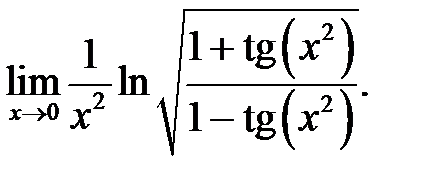
18. 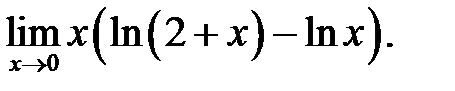
19. 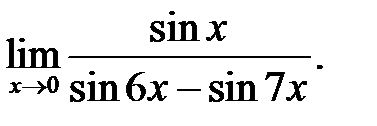
20. 
21. 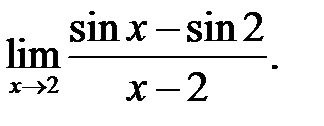
22. 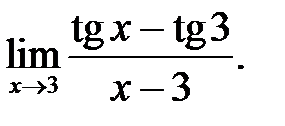
23. 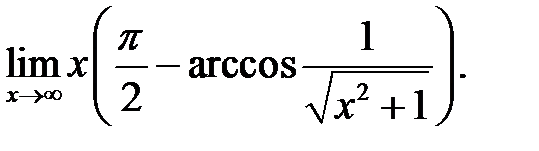
24. 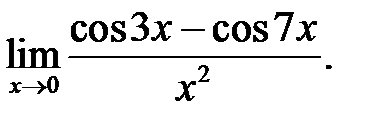
25. 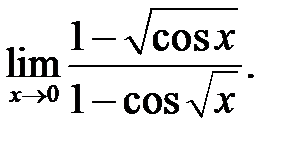
26. 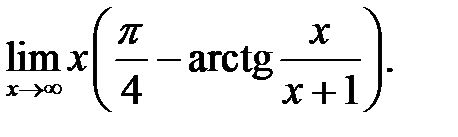
27. 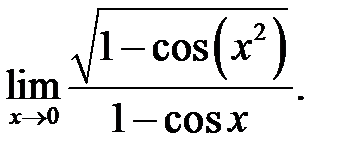
28. 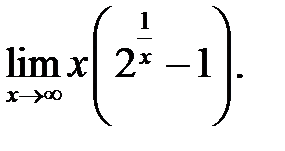
29. 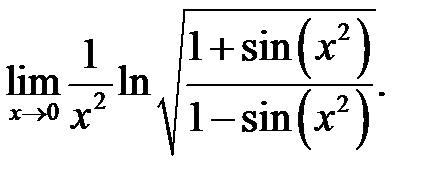
30. 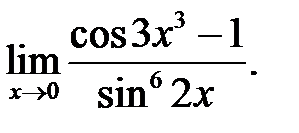
Завдання 4
Обчислити границі:
1. 
2. 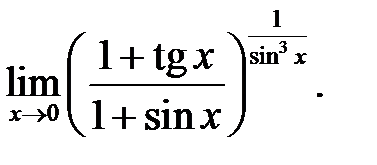
3. 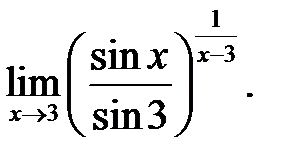
4. 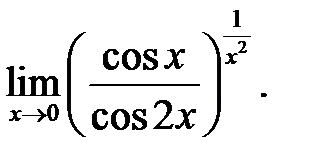
5. 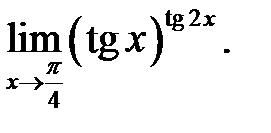
6. 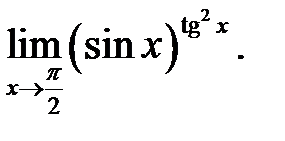
7. 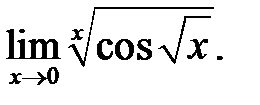
8. 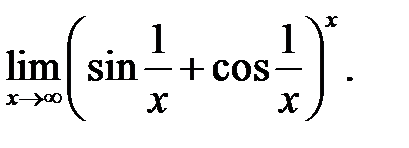
9. 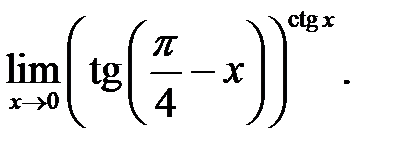
10. 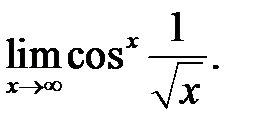
11. 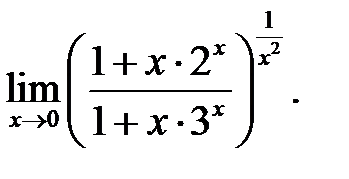
12. 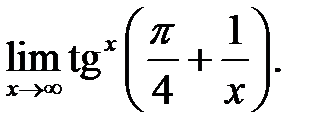
13. 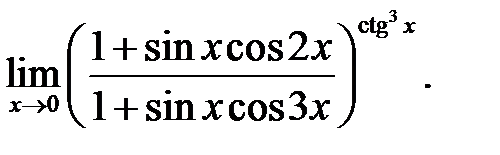
14. 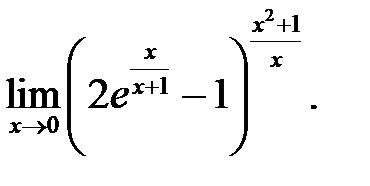
15. 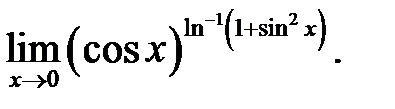
16. 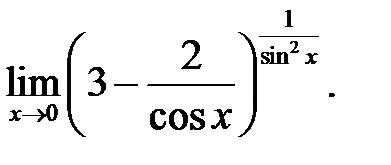
17. 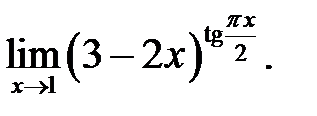
18. 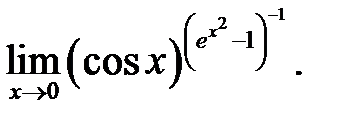
19. 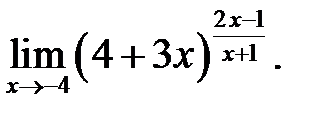
20. 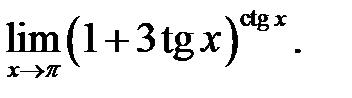
21. 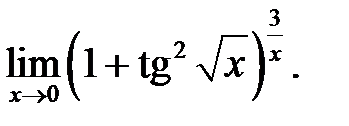
22. 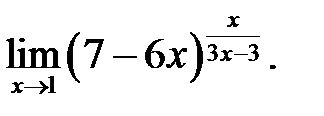
23. 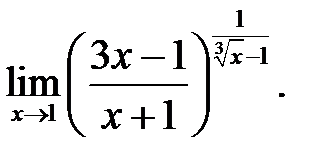
24. 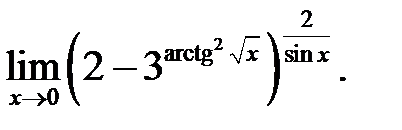
25. 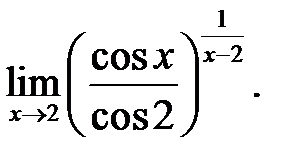
26. 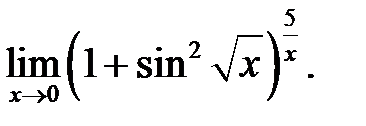
27. 
28. 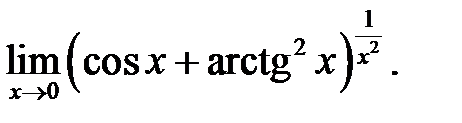
29. 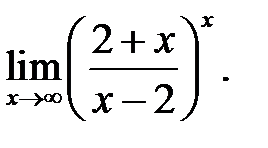
30. 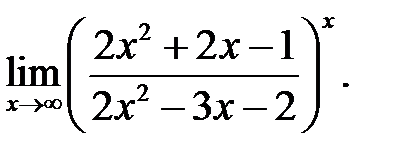
Завдання 5
Знайти порядок малості і виділити головну частину нескінченно малої функції 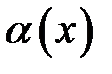 відносно
відносно  при
при 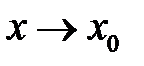 .
.
1. 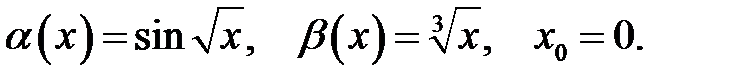
2. 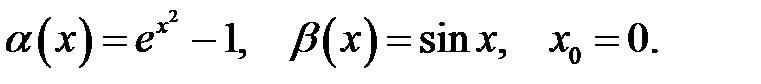
3. 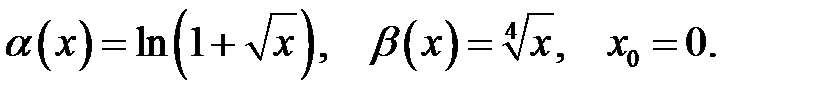
4. 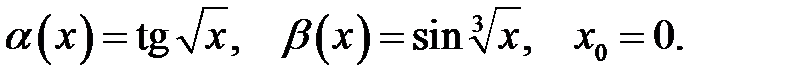
5. 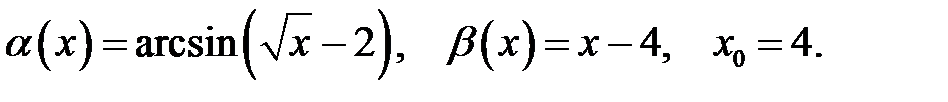
6. 
7. 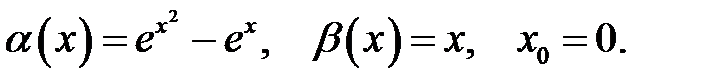
8. 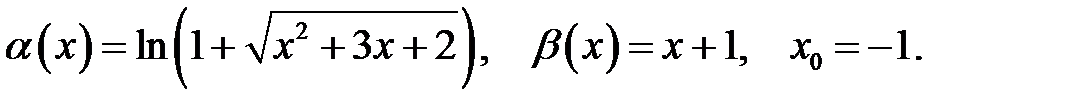
9. 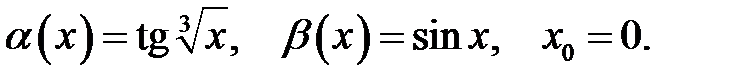
10. 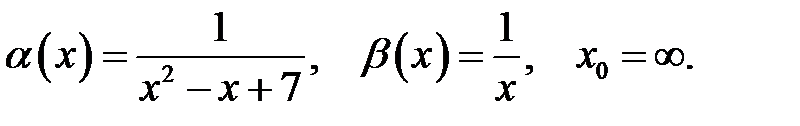
11. 
12. 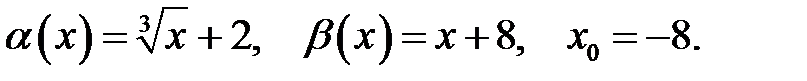
13. 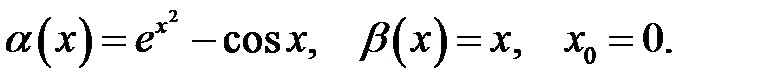
14. 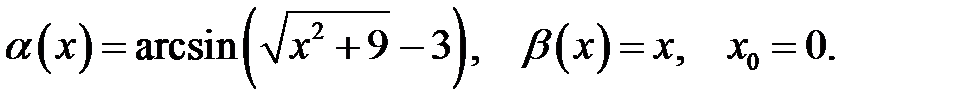
15. 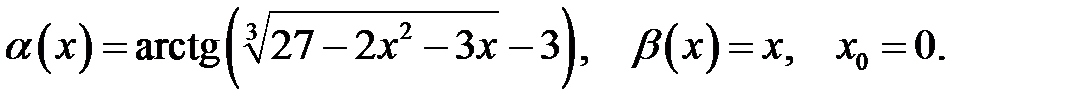
16. 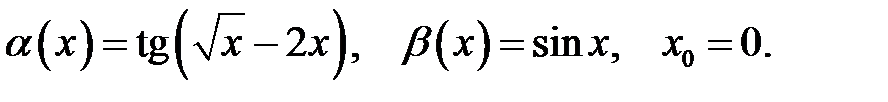
17. 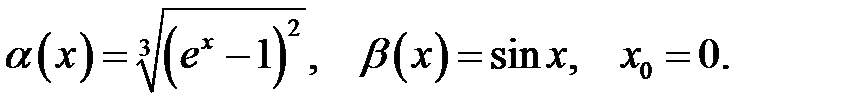
18. 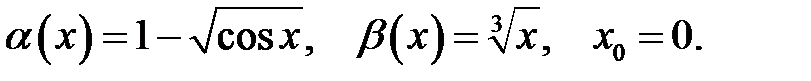
19. 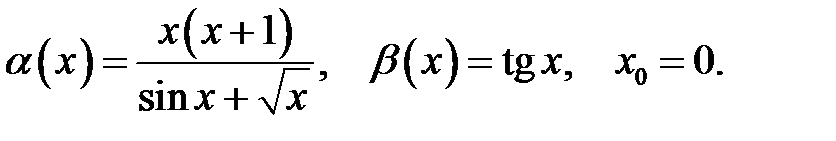
20. 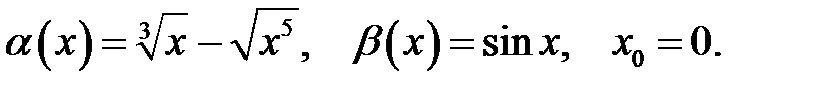
21. 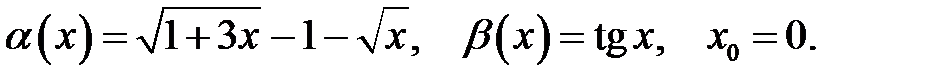
22. 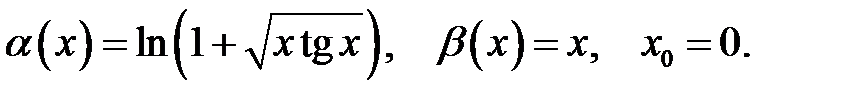
23. 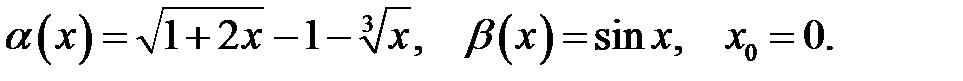
24. 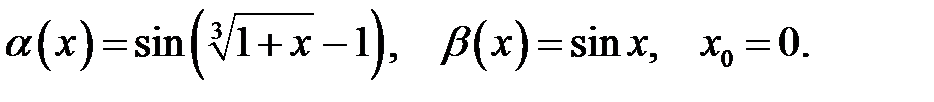
25. 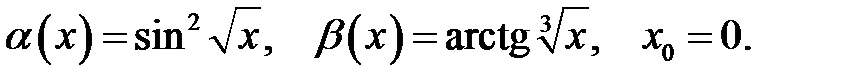
26. 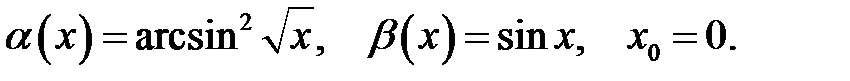
27. 
28. 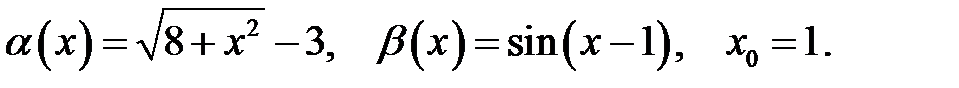
29. 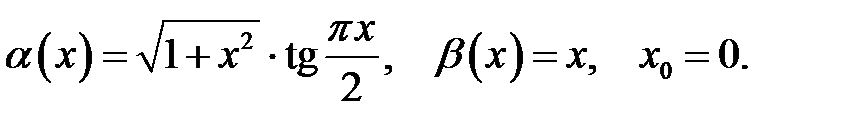
30. 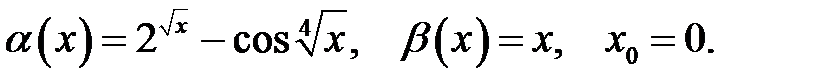
Завдання 6
Знайти порядок росту і виділити головну частину нескінченно великої функції 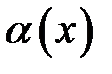 відносно
відносно  при
при 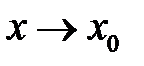 .
.
1. 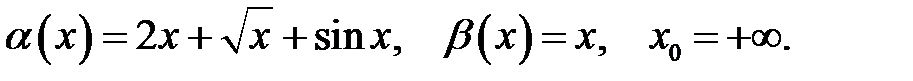
2. 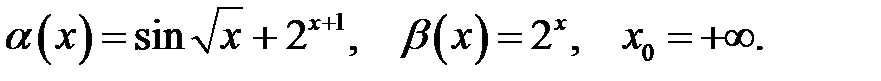
3. 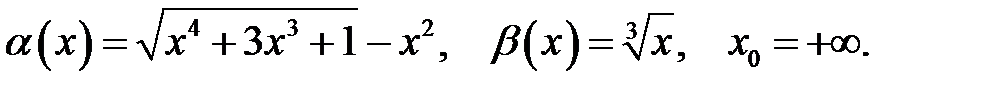
4. 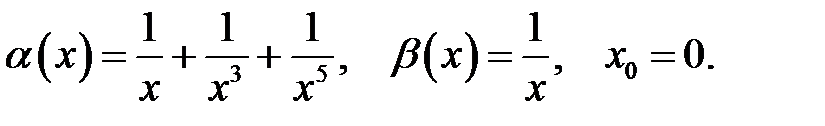
5. 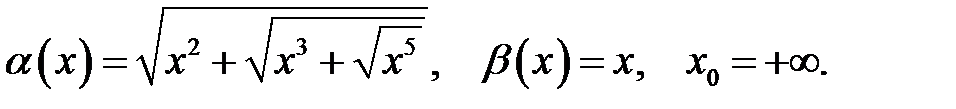
6. 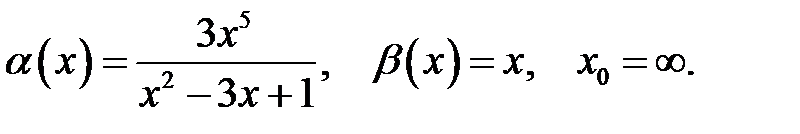
7. 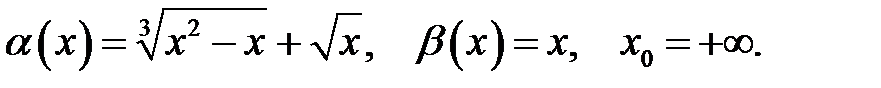
8. 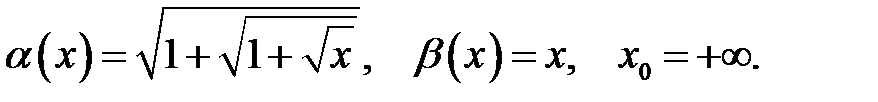
9. 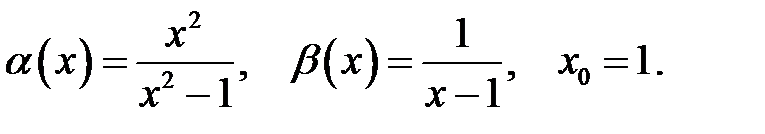
10. 
11. 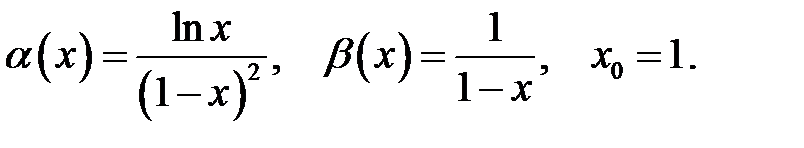
12. 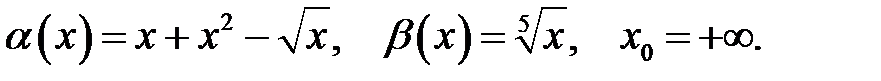
13. 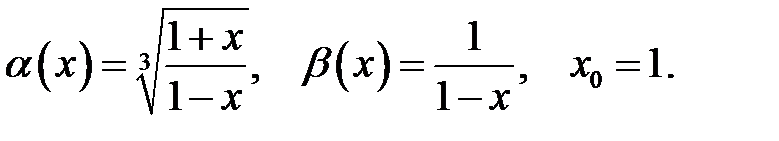
14. 
15. 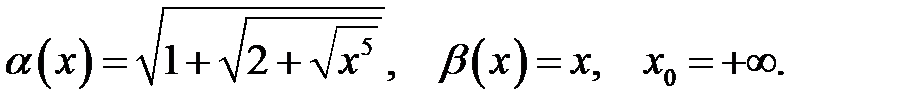
16. 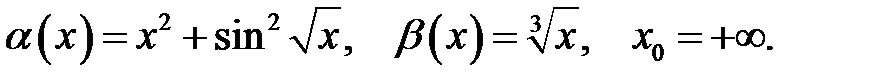
17. 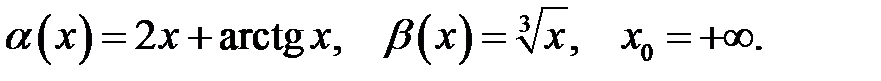
18. 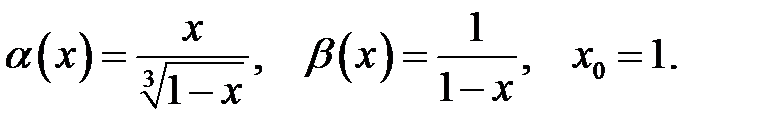
19. 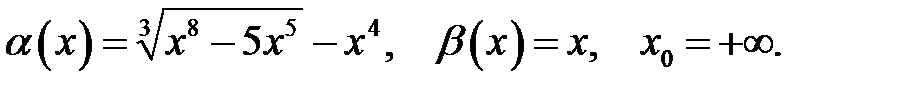
20. 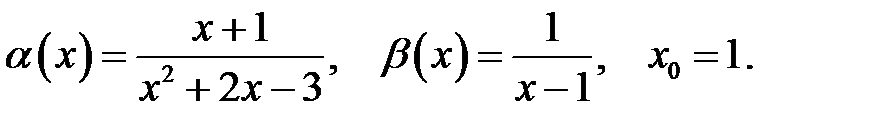
21. 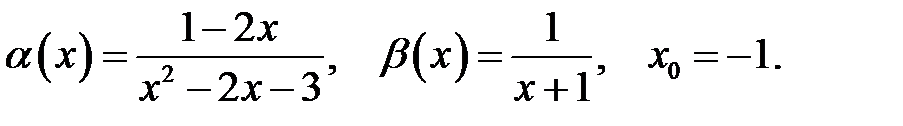
22. 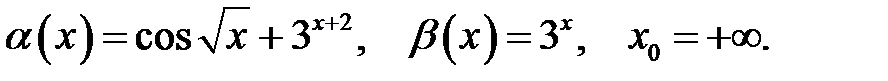
23. 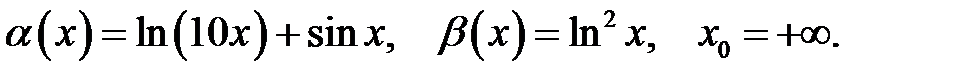
24. 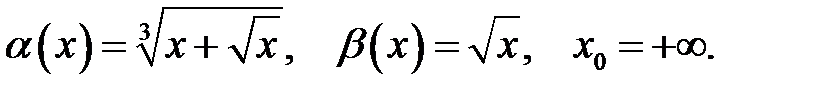
25. 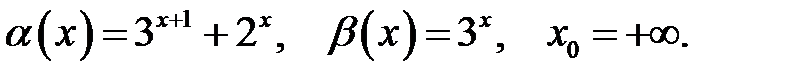
26. 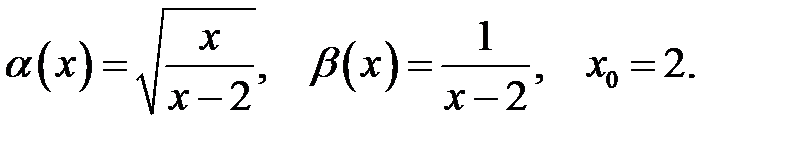
27. 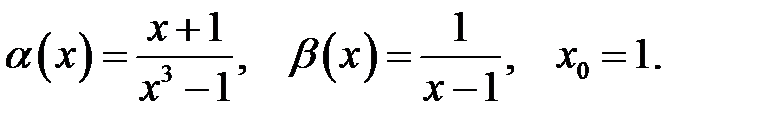
28. 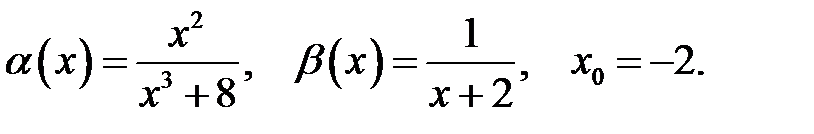
29. 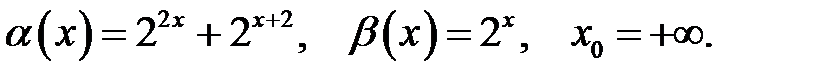
30. 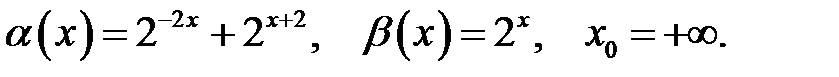
Читайте також:
- Адвокатура в Україні: основні завдання і функції
- Алгоритм знаходження ДДНФ (ДКНФ) для даної булевої функції
- Але відмінні від значення функції в точці або значення не існує, то точка називається точкою усувного розриву функції .
- Аналіз коефіцієнтів цільової функції
- АРХІВНІ ДОВІДНИКИ В СИСТЕМІ НДА: ФУНКЦІЇ ТА СТРУКТУРА
- АРХІВНІ ДОВІДНИКИ В СИСТЕМІ НДА: ФУНКЦІЇ ТА СТРУКТУРА
- Асимптоти графіка функції
- Асимптоти графіка функції
- Базальні ядра, їх функції, симптоми ураження
- Базові функції, логічні функції
- Банки як провідні суб’єкти фінансового посередництва. Функції банків.
- Банківська система та її основні функції
| <== попередня сторінка | | | наступна сторінка ==> |
| Границя послідовності | | | Неперервність функції |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |