• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Границя послідовності

Відображення множини натуральних чисел у множину дійсних чисел називається числовою послідовністю, тобто 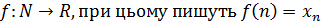. Вживають також позначення:

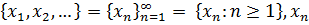– називають членом послідовності, а - номером цього члена. Послідовність називається обмеженою, якщо множина обмежена. Тобто 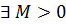таке, що для Послідовність необмежена, якщо множина

необмежена, або .

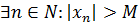Означення (границі послідовності за Коші)

Число називається границею послідовності 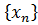, якщо для таке, що для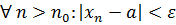

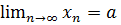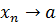Записують або при .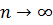

З геометричної точки зору це означає, що довільний -окіл точки 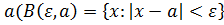містить безліч членів послідовності, а зовні цього околу лежить хіба що скінченне число членів послідовності.

Послідовність, яка має скінченну границю називається збіжною, і розбіжною в протилежному випадку.

Означення (фундаментальної послідовності).

Послідовність 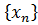називається фундаментальною, якщо для таке, що і 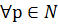виконується нерівність .

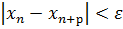Теорема. (Критерій Коші збіжності послідовності).

Для того, щоб послідовність була збіжною необхідно і достатньо, щоб вона була фундаментальною.

Зауваження При розв’язанні наступних задач часто буде використовуватися поняття цілої частини числа , позначається – найбільше ціле число, яке не перевищує .

Приклад1. Користуючись означенням границі послідовності за Коші довести, що

Виберемо довільне і розглянемо модуль різниці між -им членом послідовності і числом

Згідно з означенням границі послідовності ми повинні вказати номер 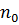(залежний від ) такий, що виконується нерівність

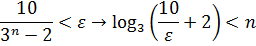
Для того, щоб вказати номер 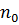досить взяти цілу частину числа тобто . Дійсно, якщо 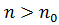, то

Таким чином, для довільного існує номер 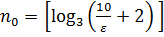такий, що для всіх номерів 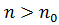виконується нерівність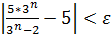
Приклад 2. Користуючись критерієм Коші довести збіжність послідовності , де .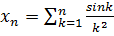

Згідно з критерієм Коші збіжності послідовності досить показати, що послідовність є фундаментальною. Оцінимо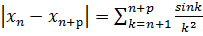

Оскільки 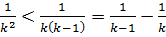, то

=

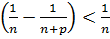
Таким чином для довільних маємо .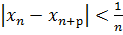

Виберемо довільне і за 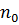виберемо цілу частину числа , тобто 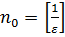. Тоді для всіх

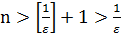маємо 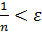. Отже для довільного 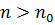і довільного 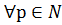виконується нерівність .

Приклад 3.Користуючись критерієм Коші довести, що послідовності , де 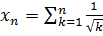є розбіжною.

Доведемо, що послідовність не є фундаментальною.

Розглянемо 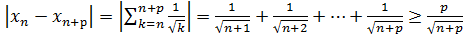(кожен з доданків оцінено найменшим за величиною останнім доданком).

Покладемо ( 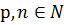) , тоді , для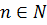

Остання оцінка показує, що при яке б не було 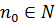, для всіх 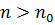і довільного натурального числа 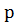(візьмемо p=n) виконується нерівність

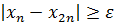тобто послідовність не є фундаментальною, а отже є розбіжною.

Послідовність 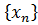називається нескінченно малою (НМ), якщо 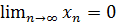. Послідовність 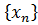називається нескінченно великою (НВ), якщо для 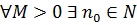такий, що для всіх 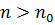виконується 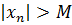і записують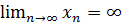

При розв’язуванні задач використовуються наступні властивості НМ, НВ, а також збіжних послідовностей:

1. Алгебраїчна сума скінченного числа НМ послідовностей є НМ послідовність

2. Добутком НМ послідовності на обмежену послідовність є НМ послідовність

3. Якщо 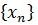НВ (НМ) послідовність , то послідовність є НМ(НВ) послідовністю. Зокрема 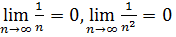тощо

4. Якщо і ,то

А)

Б)

В)якщо ,

і .

Приведемо також три теореми.

Теорема 1(про проміжну послідовність). Якщо 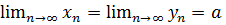і, починаючи з певного номера виконується нерівність тоді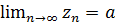

Теорема (Штольца)Якщо послідовності і задовольняють умовам:

1) при

2)

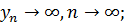
3) (причому може дорівнювати ). Тоді

Читайте також:

1. Визначений інтеграл, як границя інтегральних сум
2. Визначення послідовності вогнепальних поранень.
3. Визначення послідовності обробки поверхонь заготовки
4. Виявлення послідовності
5. Встановлення факту віднесення аварійної події до рангу НС, ви­значення виду та рівня НС проводиться у такій послідовності.
6. ГРАНИЦЯ САМОЗАЙМАННЯ
7. Границя функції
8. Границя функції
9. Границя функції двох змінних
10. Границя функції на нескінченності
11. Границя функції. Означення границі функції за Гейне й за Коші.

Переглядів: 3526