• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Відношення порядку

Означення 1.3.14. Бінарне відношення R називають відношенням строгого порядку, коли воно антисиметричне і транзитивне. Позначають: 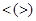або .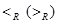

Отже R – відношення строгого порядку, якщо:

1) ;

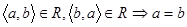2) .

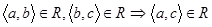Наприклад, розташування символів у довільному скінченному алфавіті означує відношення строгого лексикографічного порядку, яке лежить в основі впорядкування словників, енциклопедій, індексів, довідників, списків, таблиць тощо.

Означення 1.3.15. Якщо відношення порядку є рефлексивним ( ), то його називають відношенням часткового (нестрогого) або квазіпорядку. Позначають: або .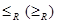

Наприклад, у числових множинах N, Q, R встановлено відношення строгого ( 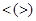) і нестрогого ( ) порядку.

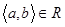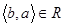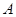Множину M, на якій задано відношення порядку, називають впорядкованою, аелементи a,bÎM – порівнюваними за відношенням R, якщо виконується або . Запис означає, що у множині відношення порядку .

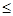Впорядковану множину M, в якій будь-які різні два елементи є порівнюваними між собою, називають лінійно впорядкованою множиною або ланцюгом. Відповідне відношення R (як строге, так і нестроге), задане на лінійно впорядкованій множині, називають лінійним (досконалим) порядком.

Очевидно, відношення рівності є відношенням часткового порядку на будь-якій множині M, цей порядок називають тривіальним.

Теорема 1.3.3. Якщо 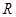– відношення строгого (нестрогого) порядку, то обернене відношення 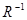– теж відношення строгого (нестрогого) порядку.

Нехай M частково впорядкована множина і A деяка непорожня підмножина множини M.

Означення 1.3.16. Верхньою гранню підмножини AÍM в множині M називається елемент bÎM такий, що a£b всіх aÎA. Елемент b називається найбільшим елементом множини M, якщо b – верхня грань множини M. Відповідно, елемент c частково впорядкованої множини M називається нижньою гранню підмножини AÍM, якщо c£a для будь-якого aÎA. Елемент c – найменший в множині M, якщо c – нижня грань самої множини M.

Означення 1.3.17. Елемент xÎM називається максимальним в множині M, якщо не існує елемента aÎM такого, що x<a. Відповідно, елемент nÎM називається мінімальним у множині M, якщо не існує елемента aÎM такого, що a<n.

У лінійно впорядкованій множині поняття найбільшого і максимального (найменшого і мінімального) елементів збігаються.

Читайте також:

1. RLC-фільтр четвертого порядку
2. Аналіз співвідношення активів із джерелами їх фінансування
3. Антонімічні відношення
4. Аспекти організаційного порядку
5. Афінний шифр k-ro порядку.
6. Багатовимірність людського буття: співвідношення біологічного і соціального в людині
7. Безрозмірною характеристикою гідротрансформатора називається залежність коефіцієнтів пропорційності моментів насосного і турбінного коліс від його передаточного відношення.
8. Бінарне відношення порядку.
9. Бінарні відношення
10. Благами вищого порядку є засоби виробництва. До останніх Менгер також відносив «користування капіталом і діяльність підприємців».
11. Будь яка передача характеризується передаваємою потужністю та передаточним відношенням.
12. Варіанти співвідношення потреб і виробництва

Переглядів: 3200