
МАРК РЕГНЕРУС ДОСЛІДЖЕННЯ: Наскільки відрізняються діти, які виросли в одностатевих союзах
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
Контакти
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Визначення булевої функції
Визначення 4.1. Булевою функцією f(x1, x2, ... , xn) називається довільна функція n змінних, аргументи якої x1, x2, ... , xn і сама функція f приймає значення 0 або 1, тобто xi 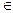 {0, 1}, i = 1, 2, ... , n; f(x1, x2, ... , xn)
{0, 1}, i = 1, 2, ... , n; f(x1, x2, ... , xn) 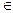 {0, 1}.
{0, 1}.
Будь-яка булева функція може бути представлена таблицею, у лівій частині якої перераховані всі набори змінних (їх 2n), а в правій частині – значення функції. Приклад такого завдання представлений у таблиці 4.1.
Таблиця 4.1
| x1 x2 x3 | f(x1, x2, x3) |
| 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 |
Для формування стовпця значень змінних зручний лексико-графічний порядок, відповідно до якого кожен наступний набір значень виходить із попереднім додатком 1 у двійковій системі числення, наприклад, 100 = 011+ 1.
Всього існує 22 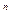 різних булевих функцій n змінних.
різних булевих функцій n змінних.
Функцій однієї змінної – 4. З них виділимо функцію “заперечення x”(позначається Øx). Ця функція представлена в таблиці 4.2.
 Таблиця 4.2
Таблиця 4.2
| x | Øx |
Булевих функцій двох змінних – 16 (22 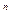 при n = 2). Ті з них, які мають спеціальні назви, представлені в таблиці 4.3.
при n = 2). Ті з них, які мають спеціальні назви, представлені в таблиці 4.3.
Таблиця 4.3
| x1 x2 | x1Vx2 | x1& x2 | x1 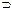 x2 x2
| x1~x2 | x1 Å x2 | x1¯ x2 | x1ï x2 |
| 0 0 0 1 1 0 1 1 | 0 | 1 | 1 |
У таблиці 4.3 представлені наступні функції двох змінних:
x1Vx2 – диз’юнкція;
x1& x2 – кон’юнкція;
x1Éx2 – імплікація;
x1~x2 – еквівалентність;
x1Å x2 – додавання по модулі 2;
x1¯x2 – стрілка Пірса;
x1ï x2 – штрих Шеффера.
Інші функції спеціальних назв не мають і можуть бути виражені через перераховані вище функції.
Читайте також:
- CMM. Визначення моделі зрілості.
- I визначення впливу окремих факторів
- II. Визначення мети запровадження конкретної ВЕЗ з урахуванням її виду.
- II. Мотивація навчальної діяльності. Визначення теми і мети уроку
- Ocнoвнi визначення здоров'я
- S Визначення оптимального темпу роботи з урахуванням динаміки наростання втоми.
- А. Визначення розмірів і площі зони хімічного зараження.
- Автоматизоване робоче місце (АРМ) бухгалтера: призначення, функції та його рівні
- Адвокатура в Україні: основні завдання і функції
- Адміністративна відповідальність: поняття, мета, функції, принципи та ознаки.
- Алгебраїчний спосіб визначення точки беззбитковості
- Алгоритм визначення проекцій точок на поверхнях обертання
| <== попередня сторінка | | | наступна сторінка ==> |
| Розділ 4. | | | Формули логіки булевих функцій |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |