• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Резонанс напруг. Добротність послідовного коливального контуру

Повернемося до виразу (4.16) для кола, схему якого зображено на рис. 4.27.

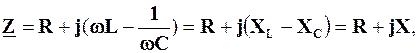
де X=X_L-X_C.

Підбираючи величини w, L та С, можна добитися того, що реактивні опори індуктивного та ємнісного елементів дорівнюватимуть один одному:

X_L = X_C = X₀. (4.17)

При цьому реактивний опір усього кола дорівнюватиме нулю:

X = X_L – X_C = X₀ – X₀ = 0,

а комплексний опір буде чисто активним і дорівнюватиме величині R:

Z = R + j(X₀-X₀) = R+j0 = R.

Повний опір також дорівнюватиме величині активного опору:

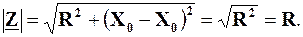
Крім того, з виразу 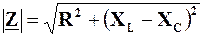випливає, що R є мінімальним значенням, яке може приймати величина повного опору. Наприклад, якщо залишити недоторканими L та C і змінювати лише величину w, то величина 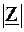змінюватиметься так, як показано на рис.4.28. Рівність X_L=X_C виконується на деякій кутовій частоті w₀. На цій же частоті аргумент комплексного опору дорівнюватиме нулю:

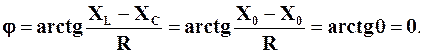
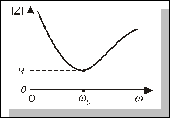
рис. 4.28

У підрозділі 4.5.1 вже показано, що початкова фаза струму обчислюється як 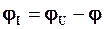, тому при виконанні умови X_L=X_C маємо:

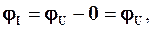
тобто за вказаної умови струм співпадає за фазою з напругою.

Режим роботи кола, утвореного послідовно з’єднаними індуктивним та ємнісним елементами (наявність резистора не є обов’язковою), при якому реактивний опір кола дорівнює нулю, називається резонансом напруг.

Кутову частоту w₀, на якій має місце резонанс напруг, називають резонансною кутовою частотою.

Коло, схему якого зображено на рис. 4.27, називають послідовним коливальним контуром.

За означенням, при резонансі напруг на частоті w₀ маємо 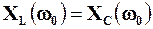, тобто 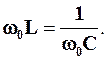Звідси отримуємо дуже важливі для розрахунку пристроїв автоматики та зв’язку формули:

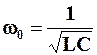(4.18)

та

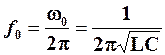. (4.19)

Ці формули визначають величину резонансної частоти через параметри конденсатора та котушки, що складають послідовний коливальний контур.

Згідно з (4.17) та (4.18) маємо:

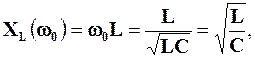
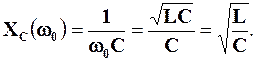
Величину 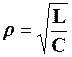називають характеристичним опоромпослідовного коливального контуру.

Оскільки крізь індуктивний та ємнісний елементи контуру протікає один і той самий струм, то при резонансі маємо рівні діючі значення (або амплітуди) напруг на цих елементах:

.

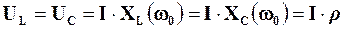Але 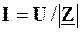, до того ж при резонансі 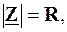тому в цьому режимі 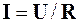. Тоді .

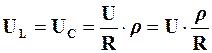Введемо добротністьпослідовного коливального контуру

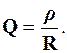
Тоді при резонансі напруг діюче значення вхідної напруги пов’язане з діючими значеннями напруг на індуктивному та ємнісному елементах як

U_L = U_C = Q×U.

У пристроях автоматики та зв’язку величина r, як правило, набагато більша за R, тому в них Q>>1. Отже, при резонансі напруг величини напруг на індуктивному та на ємнісному елементах послідовного коливального контуру в Q раз більші ніж вхідна напруга U, що й обумовило назву “резонанс напруг” для розглянутого режиму роботи кола.

Змінюватимемо подумки частоту вхідної напруги при постійних R, L, С та U. Якщо w < w₀,то X_L= wL < r (боX_L зростає з частотою і сягає величини r, коли w досягне w₀), а 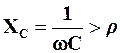. При цьому аргумент комплексного опору контуру є від’ємним, бо

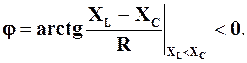
Тому початкова фаза струму 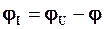є більшою за початкову фазу напруги j_U. Тобто, при w < w₀ струм випереджає вхідну напругу за фазою. Кажуть, що за цієї обставини опір послідовного коливального контуру має ємнісний характер.

Векторні діаграми напруг та струмів для розгляданого випадку w < w₀ наведено на рис. 4.29[3]. Заштрихований прямокутний трикутник з катетами U_X та U_R і гіпотенузою U називають трикутником напруг.

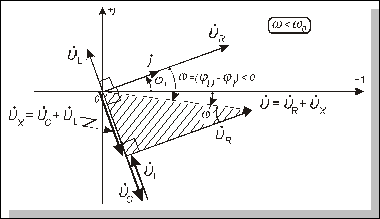
Рис. 4.29

На рис. 4.30 графічно проілюстровані співвідношення між активною та реактивною складовими комплексного опору Z послідовного коливального контуру за умови, що w < w₀. Заштрихований на цьому рисунку трикутник називають трикутником опорів.З нього наочно випливає, що .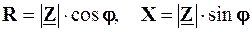

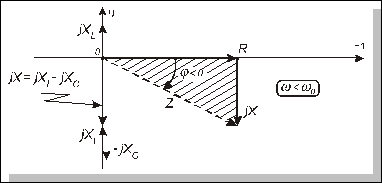
Рис. 4.30

Аналогічним чином для випадку w > w₀ можна показати, що величина j буде додатною і опір послідовного коливального контуру матиме індуктивний характер. Нескладно зробити й графічні побудови, аналогічні показаним на рис.4.29 та рис. 4.30.

У випадку, коли w = w₀ (тобто при резонансі напруг) маємо 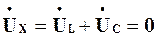та jX=j(X_L-X_C)=0, і на відповідних векторних діаграмах залишаються тільки активна складова напруги 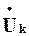та активний опір R.

Читайте також:

1. Аналіз послідовного інтерфейсу з DSP-процесорами
2. Вибір елементів пуско-гальмівного реостата для двигунів послідовного збудження
3. Вибірні властивості коливального контуру
4. Визначення запасів стійкості внутрішнього контуру
5. Вплив послідовного і шунтуючого опору на вольт-амперну характеристику сонячного елемента
6. Встановлення заземлень і захисту від перенапруг.
7. Ділення виду 80:20, 600:30, 600:300 способом послідовного ділення та способом випробовування.
8. Ділення числа на добуток. Спосіб послідовного ділення. Розв'язуваня задач.
9. Діюче, середнє та середнє за модулем значення струмів і напруг.
10. Для резонансних частот можливо записати
11. Дослідження резонансних кіл
12. ДОСЛІДЖЕННЯ РЕЗОНАНСНИХ ЯВИЩ

Переглядів: 5226